| Transition Temperature | 17.5 K |
|---|---|
| Experiment Temperature | 1.5 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pca21 (#29) |
| Magnetic Space Group | Pc'a21' (#29.101) |
| Magnetic Point Group | m'm2' (7.3.22) |
| Lattice Parameters | 8.542(4) 8.573(4) 12.090(6) 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1080/00150199408245095 |
| Reference | P. Schobinger-papamantellos, P. Fischer, F. Kubel and H. Schmid, Ferroelectrics (1994) 162 93-101. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Co1 | Co | 4.7 | 0.0 | 0.0 | 4.70 |
| Co2 | Co | 0.0 | 1.6 | -3.7 | 4.03 |
| Co3 | Co | 0.0 | -1.6 | 0.6 | 1.71 |
This article was downloaded by: [University of Tasmania] On: 13 January 2015, At: 22:13 Publisher: Taylor & Francis Informa Ltd Registered in England and Wales Registered Number: 1072954 Registered office: Mortimer House, 37-41 Mortimer Street, London W1T 3JH, UK

Ferroelectrics
Publication details, including instructions for authors and subscription information: http://www.tandfonline.com/loi/gfer20
Investigation of magnetic structure and phase transitions in \( Co_{3} \)
\( ^{11} \) B \( _{7} \) O \( _{13} \) Br boracite by neutron diffraction
P. Schobinger-papamantellos \( ^{a} \) , P. Fischer \( ^{b} \) , F. Kubel \( ^{c} \) & H. Schmid \( ^{c} \)
\( ^{a} \) Institut für Kristallographie ETHZ, CH-8092, Zürich
\( ^{b} \) Labor für Neutronenstreuung, ETH Zürich und Paul Scherrer Institut, CH-5232, Villigen, PSI
\( ^{c} \) Département de chimie minérale, analytique et appliquée, Université de Genève, CH-1211, Genève, Switzerland
Published online: 25 Feb 2011.
To cite this article: P. Schobinger-papamantellos, P. Fischer, F. Kubel & H. Schmid (1994) Investigation of magnetic structure and phase transitions in \( Co_{3} \) \( {}^{11}B_{7}O_{13}Br \) boracite by neutron diffraction, Ferroelectrics, 162:1, 93-101, DOI: 10.1080/00150199408245095
To link to this article: http://dx.doi.org/10.1080/00150199408245095
PLEASE SCROLL DOWN FOR ARTICLE
Taylor & Francis makes every effort to ensure the accuracy of all the information (the "Content") contained in the publications on our platform. However, Taylor & Francis, our agents, and our licensors make no representations or warranties whatsoever as to the accuracy, completeness, or suitability for any purpose of the Content. Any opinions and views expressed in this publication are the opinions and views of the authors, and are not the views of or endorsed by Taylor & Francis. The accuracy of the Content should not be relied upon and should be independently verified with primary sources of information. Taylor and Francis shall not be liable for any losses, actions, claims, proceedings, demands, costs, expenses, damages, and other liabilities whatsoever or howsoever caused arising directly or indirectly in connection with, in relation to or arising out of the use of the Content.
This article may be used for research, teaching, and private study purposes. Any substantial or systematic reproduction, redistribution, reselling, loan, sub-licensing, systematic supply, or distribution in any form to anyone is expressly forbidden. Terms & Conditions of access and use can be found at http://www.tandfonline.com/page/terms-and-conditions
INVESTIGATION OF MAGNETIC STRUCTURE AND PHASE TRANSITIONS IN \( Co_{3}^{11}B_{7}O_{13}Br \) BORACITE BY NEUTRON DIFFRACTION
P. SCHOBINGER-PAPAMANTELLOS, \( ^{a} \) P. FISCHER, \( ^{b} \) F. KUBEL \( ^{c} \) and H. SCHMID \( ^{c} \)
\( ^{a} \) Institut für Kristallographie ETHZ, CH-8092 Zürich;
\( ^{b} \) Labor für Neutronenstreuung, ETH Zürich und Paul Scherrer Institut, CH-5232 Villigen PSI; \( ^{c} \) Département de chimie minérale, analytique et appliquée, Université de Genève CH-1211 Genève, Switzerland
(Received September 13, 1993; in final form December 23, 1993)
Neutron diffraction investigations of orthorhombic \( Co_{3}^{11}B_{7}O_{13}Br \) at 293 K and in the temperature range 1.5–30 K reveal a two step onset of magnetic ordering, starting at the second order transition to a weakly ferromagnetic phase at \( T_{N}=17.5 \) K (Néel type) and followed at about \( T_{r}=10.5 \) K, by a smooth transformation to a three-dimensional canted magnetic structure (magnetic space group \( Pc^{\prime}a2_{1}^{\prime}(Sh_{10}^{10}) \) ), magnetic modes \( C_{x}(++--) \) , \( F_{x}(++++) \) , \( A_{z}(+-+) \) . The three Co sites display completely different moment values and directions, arising from frustration effects associated with the formation of isolated \( Co_{3}Br \) groups with a triangular arrangement of the three Co sites.
Keywords: Bozacite, neutron diffraction, magnetic structure, ferroelectric, ferromagnetic, ferroelastic.
1. INTRODUCTION
Members of the boracite family \( M_{3}B_{7}O_{13}X \) (where M stands for a bivalent transition metal ion and X for Cl, Br, I) are of particular interest due to their simultaneously ferroelectric/ferroelastic weakly ferromagnetic phases and their magnetoelectric and optical properties. \( ^{1,2} \) Depending on the nature of the substituents various sequences of phase transitions occur, consisting in subtle structural changes, which in turn govern the magnetic behaviour.
In analogy to the mineral \( Mg_{3}B_{7}O_{13}Cl^{3+} \) the \( Co_{3}B_{7}O_{13}X \) (Co—X, X—Cl, Br, I) boracites are known to undergo a first-order phase transition from a paramagnetic-paraelectric cubic phase \( F\bar{4}3c1' \) (Z = 8) to an orthorhombic paramagnetic fully ferroelectric/fully ferroelastic phase \( Pca2_{1}1' \) (Z = 4) at temperatures 623 K, 466 K and \( \approx194 \) K, respectively. \( ^{1,5} \) This transition involves a doubling of the cubic primitive unit cell and a threefold splitting of the Co site. At lower temperatures (11.5 K, 17.5 K and 38 K, respectively) all three compounds undergo a magnetic phase transition and display weakly ferromagnetic ordering. \( ^{6,7,8b,8c,9a,9b} \) On the basis of the magnetoelectric effect of \( Co—Br^{8} \) and \( Co—I^{8a} \) boracites the magnetic point group for both compounds was found to be \( m'm2' \) down to 4.2 K, while the \( Co—Cl \) boracite undergoes two further improper structural transitions, to monoclinic point symmetry \( m1' \) (at 538 K) and trigonal 3m1' (at 468 K), before it orders magnetically at 11.5 K in the monoclinic Shubnikov group m which allows (weak) ferromagnetism. \( ^{8b} \)
Specific heat measurements \( ^{9} \) indicate that all three compounds display a “Schottky anomaly” at temperatures lower than \( T_{N} \) . For the Co—I compound \( ^{10} \) this Schottky anomaly has been interpreted on the basis of neutron diffraction results as a spin reorientation without any further change of the magnetic symmetry. It is of interest to extend this study to the other two members of the Co—X family, for which no neutron diffraction studies have previously been reported. In the present paper we will report on the magnetic ordering and the sequence of phase transitions occurring in Co—Br boracite, following the scheme:
\[ \mathrm{F}43\mathrm{cl}^{1}\mathrm{~(cubic)}\xleftarrow{466\mathrm{~K}}\mathrm{Pca}_{2}\mathrm{I}^{1}\mathrm{~(orthorhombic)}\xleftarrow{T_{N}=17.5\mathrm{~K}}\mathrm{m}^{1}\mathrm{m}^{2}\xleftarrow{T_{I}=10\mathrm{~K}}\mathrm{m}^{2}\mathrm{~(orthorhombic)} \]
2. EXPERIMENTAL AND RESULTS
The neutron measurements (using single phase powder samples obtained by crushing single crystals), were performed by means of the "DMC" (double axis multi-counter diffractometer) and the two-axis spectrometer at the reactor Saphir in Wuerenlingen, at 293 K and in the temperature range 1.5–30 K ( \( \lambda = 1.70012 \AA \) ), cf. Figures 1 and 2. The step increment of the diffraction angle \( 2\theta \) was \( 0.10^{\circ} \) . In order to avoid high absorption, the \( {}^{11}B \) isotope and an annular vanadium sample holder with inner and outer diameters of 10 and 12 mm, respectively, were used. With a view to the expected weak magnetic intensities the high-intensity instrumental configuration (without primary collimation) was used. The data were corrected for absorption and evaluated by the line profile analysis method, \( ^{11-13} \) using

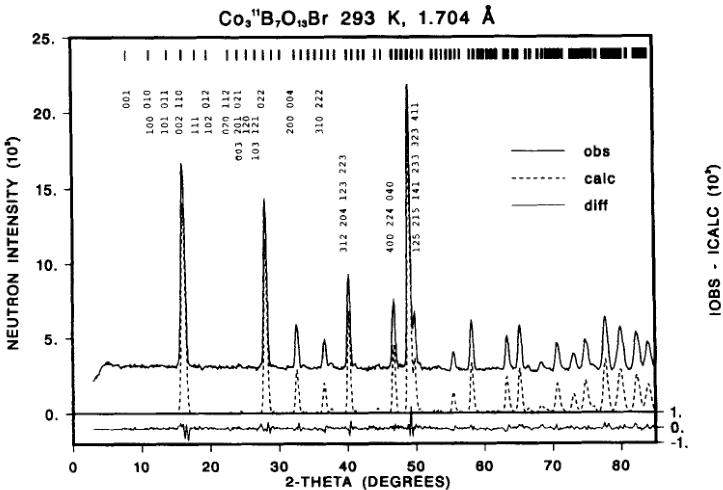
FIGURE 1 Observed, calculated and difference neutron powder patterns of orthorhombic \( Co_{3}B_{7}O_{13}Br \) boracite in the paramagnetic state (only nuclear contributions) at 293 K.

Co_{3}“B_{7}O_{35}Br 11-23 K, 1.70012 Å, Pc’a2_{i}

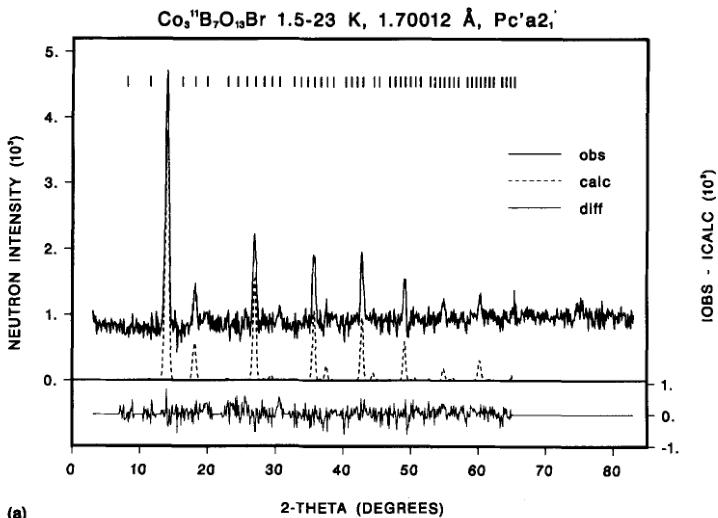
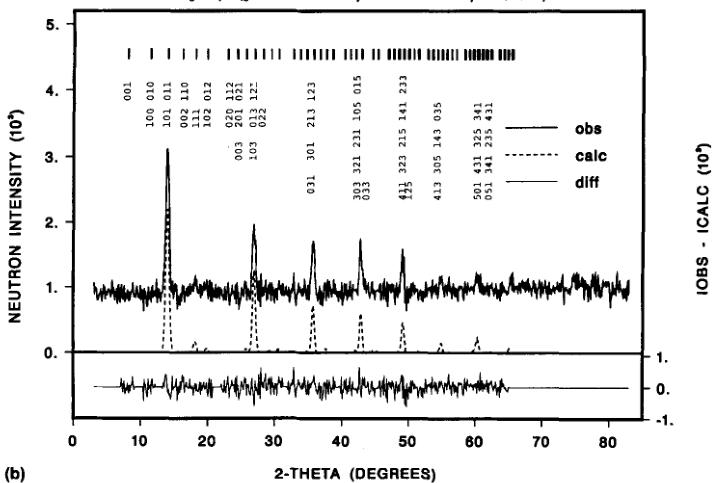
FIGURE 2 Observed, calculated and difference neutron powder patterns of \( Co_{3}B_{7}O_{13}Br \) boracite obtained by subtraction of the 23 K nuclear data from the data in the magnetically ordered state. (Only magnetic contributions) for a) 1.5–23 K (top part) b) 12–23 K (bottom part).
scattering lengths and magnetic form factors given in References 14 and 15, respectively.
2a. Nuclear Structure at 293 K
Results of the 293 K refined neutron pattern (see Figure 1) of the orthorhombic structure of Co—Br boracite in the paramagnetic state are summarised in Table I. Within three standard deviations these values are in good agreement with the recently published very accurate single crystal x-ray parameters \( ^{5} \) for the same temperature. As expected due to the limited experimental resolution, the parameters from the neutron powder data refinement have larger errors and for this reason the parameters of the Co site were not included in the refinement.
The main structural changes during the cubic to orthorhombic phase transition are: (i) the splitting of the Co site into three distinct sites (Co1, Co2, Co3) with different surroundings. The surroundings of Co2 and Co3 are similar, while that of Co1 is found to be different. \( ^{5} \) (ii) The splitting of the Co—Co distances; the found largest difference among Co—Co distances being 0.866(2) Å. (iii) A drastic symmetry reduction of the Co coordination around Br changing from octahedral to a plane (isosceles triangular) arrangement of the (Co1, Co2, Co3) sites with relatively short distances \( d_{Co1-Co3} = 3.975(2) \) Å, \( d_{Co2-Co3} = 3.850(2) \) Å and \( d_{Co2-Co3} = 3.850(2) \) A if compared to the \( d_{aver} = 4.292(2) \) Å. The three Co atoms together with the Br atom build isolated pyramids (see Figure 3). As will be shown in the
TABLE I
Refined structural parameters of Co_{3}B_{7}O_{13}Br in the paramagnetic state at 293 K. Space group Pca2_{1}1'. All atoms occupy sites 4(a)
| Atom | Parameter | |||
| x | y | z | B[Å]2 | |
| Co1 | 0.75880 | 0.25200 | 0.22890 | 0.054 |
| Co2 | 0.48821 | 0.52546 | 0.50120 | 0.054 |
| Co3 | -0.0107 | 0.02530 | 0.50270 | 0.054 |
| Br | 0.761(3) | 0.244(8) | 0.5087 | 0.7(2) |
| B1 | 0.503(5) | 0.510(6) | 0.254(4) | 0.2(1) |
| B2 | 0.265(3) | 0.250(5) | 0.501(5) | 0.2(1) |
| B3 | -0.009(5) | -0.017(6) | 0.259(4) | 0.2(1) |
| B4 | 0.457(2) | 0.244(7) | 0.354(3) | 0.2(1) |
| B5 | 0.255(5) | 0.399(5) | 0.177(6) | 0.2(1) |
| B6 | 0.910(3) | 0.739(7) | 0.830(4) | 0.2(1) |
| B7 | 0.772(4) | 0.905(5) | 0.673(6) | 0.2(1) |
| O1 | 0.244(5) | 0.264(6) | 0.241(5) | 0.4(1) |
| O2 | 0.527(6) | 0.333(6) | 0.271(5) | 0.4(1) |
| O3 | 0.374(7) | 0.329(6) | 0.429(4) | 0.4(1) |
| O4 | 0.981(6) | 0.163(6) | 0.274(5) | 0.4(1) |
| O5 | 0.318(6) | 0.373(7) | 0.077(5) | 0.4(1) |
| O6 | 0.173(5) | 0.959(7) | 0.221(5) | 0.4(1) |
| O7 | 0.142(5) | 0.169(7) | 0.427(5) | 0.4(1) |
| O8 | 0.314(5) | 0.533(6) | 0.234(4) | 0.4(1) |
| O9 | 0.169(6) | 0.129(8) | 0.066(6) | 0.4(1) |
| O10 | 0.948(5) | 0.585(6) | 0.854(5) | 0.4(1) |
| O11 | 0.545(5) | 0.916(6) | 0.850(6) | 0.4(1) |
| O12 | 0.928(5) | 0.543(7) | 0.667(5) | 0.4(1) |
| O13 | 0.578(5) | 0.964(7) | 0.647(5) | 0.4(1) |
| a, b, c in [Å] | 8.566(2) | 8.596(2) | 12.155(5) | |
| R_{In}, R_{wp} % | R_{exp}%, χ² | 5.9, 9.8 | 4.59, 4.5 | |

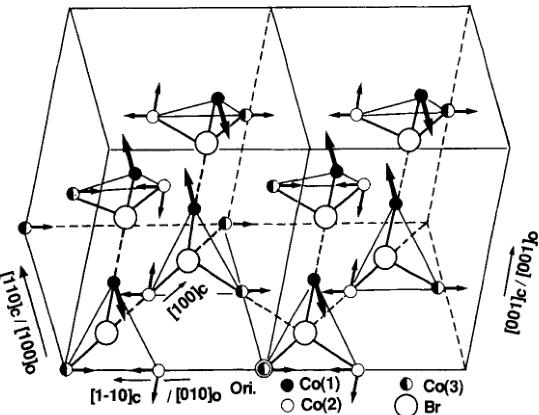
FIGURE 3 The three dimensionally canted magnetic moment arrangement of \( Co_{3}B_{7}O_{13}Br \) at 1.5 K. The small solid circles, open circles and half-solid circles denote the \( \mathrm{Co}(1) \) , \( \mathrm{Co}(2) \) and \( \mathrm{Co}(3) \) sites while the large circles represent the Br atoms.
next sections this arrangement is crucial for the presence of frustration in the spin ordering process.
2b. Magnetic Ordering
Similarly to the findings on the Co—I boracite one observes in the low temperature neutron patterns of Co—Br boracite at 1.5 K and 12 K (cf. Figure 2) additional reflections of magnetic origin at reciprocal lattice positions of the chemical cell, i.e., k = 0. The fact that the main magnetic contributions (h01)/(0k1) do not follow the limiting conditions for possible reflections of the nuclear space group (0k1, 1 = 2n and h01, h = 2n), suggests that these contributions can be attributed to antiferromagnetic ordering. There are four possible magnetic space groups \( ^{16} \) (see also Reference 2, Table II) associated with the wave vector k = 0: \( Pca2_{1} \) , \( Pc'a'2_{1} \) , \( Pca'2_{1}' \) and \( Pc'a2_{1}' \) ; however only the latter one is compatible with the magnetic point group \( m'm2' \) as derived from studies in polarized light \( ^{7} \) and from data of the magnetoelectric effect. \( ^{8} \) The \( Pc'a2_{1}' \) magnetic space group allows a three-dimensional canted moment arrangement for the three Co sublattices (all at 4(a): x, y, z; -x, -y, \( \frac{1}{2} \) + z; \( \frac{1}{2} \) + x, -y, z; \( \frac{1}{2} \) - x, y, \( \frac{1}{2} \) + z). The corresponding magnetic modes are \( C_{x}(++--) \) , \( F_{y}(++++) \) and \( A_{z}(+--+) \) . The fact that the (h01/0k1) reflections have comparable intensities indicates that the main axis of antiferromagnetism is not along the c direction. The contributions along z might then be rather small. The fact that the expected weak ferromagnetic contributions (overlapping with allowed nuclear peaks) are not observed, indicates that these are either very weak or their contributions cancel in the structure factor.
Due to the observed relatively weak magnetic contributions (compared to the nuclear ones) the refinement of the magnetic structure was carried out by using
difference diagrams between the magnetically ordered state and the paramagnetic state at 23 K. This allows a drastic reduction of the number of free parameters and therefore a more precise determination of the magnetic structure. Although the R-factors of such a refinement have rather a high value due to the larger errors on the background estimation the errors on the ordered moment values are much lower than those obtained from a refinement of all parameters of the entire pattern with essentially lower R-factors. As already mentioned above, the refined parameters of the 293 K pattern entail large errors compared with the x-ray data, (see Table I). Thus the Co positional parameters were taken from Reference 5. The lattice parameters and scale factors were obtained from a refinement of the 23 K pattern, just a few degrees above the ordering temperature.
The best agreement was obtained for the parameters given in Table II. The refinement cannot distinguish between Co(2) and Co(3) sites. Thus it is also possible that both arrangements exist in the form of domains. Due to the larger experimental error the reliability factors and the goodness of fit \( \chi^{2} \) of difference diagrams are less satisfactory than those for 293 K; however, the errors in the ordered magnetic moment values are significantly lower than those resulting from a simultaneous profile refinement with the dominant nuclear contributions.
2c. The Magnetic Structure
The 1.5 K and 12 K refined parameters (see Table II) indicate a rather different behaviour of the three Co sites: The three sites have different moment values and orientations. The dominating antiferromagnetic contribution arises from the uniaxial arrangement of the mode \( C_{x}(++- \) ) observed only for Co(1). This atom has already reached the saturation value of \( 4.5(1)\mu_{B} \) (within the error limits) at 12 K. As already mentioned one cannot distinguish between Co(2) and Co(3) sites. Co(3) has a canted moment arrangement in the (100) plane with the modes \( F_{y} \) , \( A_{z} \) and z as the main axis. Its value changes from \( 1.8(2)\mu_{B} \) at 12 K to \( 4.0(2)\mu_{B} \) at 1.5 K. The Co(3) site has essentially a weak ferromagnetic \( -F_{y} \) contribution which is antiferromagnetically coupled to Co(2). Its ordered moment value at 12 K is \( -0.80(25)\mu_{B} \) and \( 1.7(1)\mu_{B} \) at 1.5 K. Both the high temperature and the low
TABLE II
Refined parameters of magnetic ordering in Co—Br boracite from the difference neutron diagrams 1.5–23 K and 12–23 K, obtained by subtracting the paramagnetic (nuclear) intensities at 23 K from the data in the magnetically ordered state. Magnetic space group \( Pc^{\prime}a2_{1}^{\prime} \) . The positional parameters of Co are taken from the 293 K x-ray single crystal data \( ^{5} \)
| 1.5-23 K | 12-23 K | |||||
| \( \mu_{x}[\mu_{B}] \) | \( \mu_{y}[\mu_{B}] \) | \( \mu_{z}[\mu_{B}] \) | \( \mu_{T}[\mu_{B}] \) | \( \mu_{x}[\mu_{B}] \) | \( \mu y[\mu_{B}] \) | |
| Co(1) | 4.7(2) | 4.7(2) | 4.5(1) | 4.5(1) | ||
| Co(2) | 1.6(1) | -3.7(2) | 4.0(2) | 0.80(25) | -1.6(2) | |
| Co(3) | -1.6(1) | 0.6(2) | 1.7(1) | -0.80(25) | 0.80(25) | |
| a, b, c [Å] | 8.542(4), 8.573(4), 12.090(6) | 8.542(4), 8.573(4), | ||||
| \( B_{0f}[\AA]^{2} \) | 0.73(5) | 0.73(5) | ||||
| RIm, Rwp%, Rexp%, \( \chi^{2} \) , 21.8, 41.0, 11.8, 12.0 | ||||||

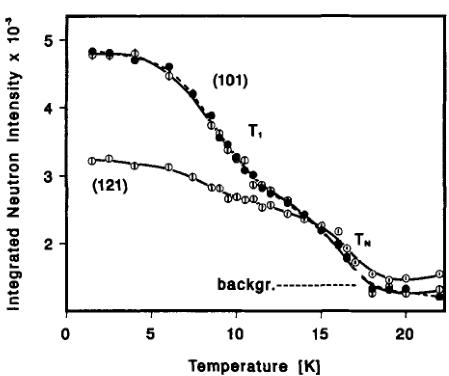
FIGURE 4 Temperature dependence of peak intensities of the magnetic reflections \( \{101\} \) and \( \{121\} \) upon heating (open symbols) and cooling (full symbols). The lines are a guide to the eyes.
temperature magnetic structures correspond to a three-dimensionally canted arrangement of the three sites as shown in Figure 3.
2d. The Temperature Dependence of Magnetic Intensities
Figure 4 displays the temperature variation of the magnetic peak intensity of the first two dominant magnetic peaks \( \{101\} \) , \( \{211, 301, 121, 103\} \) . In agreement with measurements of magnetic birefringence, \( ^{7} \) magnetoelectric effect, \( ^{8} \) specific heat \( ^{9} \) and spontaneous Faraday rotation \( ^{9a} \) the magnetic order sets in below 17.5 K. The intensity of both peaks increases smoothly up to about \( T_{r} = 10 \) K where its slope versus temperature begins to become steeper. This rather smooth change of slope is equally reflected in the analogous temperature dependence of the spontaneous Faraday rotation \( ^{9a} \) and in the change of the slope of the magnetoelectric coefficient \( \alpha_{23} \) . \( ^{8} \) From the temperature dependence of the \( \{101\} \) peak upon cooling and heating one may conclude that both phase transitions are of second order in agreement with the findings of References 7, 8 and 9a.
DISCUSSION
The present neutron diffraction results show that the onset of magnetic ordering of Co—Br boracite consists of a two step process characterised by successive ordering of the three Co sites which display different magnetic moment values and orientations as well as a different temperature behaviour.
It is noteworthy that the change of slope of the neutron intensity and of that of the spontaneous Faraday rotation is associated with a very large “Schottky anom-
aly" in the specific heat, peaking at about 8 K and spreading between about 4 and 12 K. \( ^{9} \) These facts, together with the failure to detect so far a change of point symmetry \( ^{7,8} \) below \( \approx \) 10 K, suggest that the second step of the two step ordering is spread over a rather large temperature interval. Accurate susceptibility and magnetisation measurements on ferroelastic single domains will, however, be necessary with a view to corroborating these findings.
In the temperature range \( (T_{t} Partial support by the Swiss National Science Foundation is gratefully acknowledged. H. Schmid and H. Tippemann, Ferroelectrics, 20, 21 (1978). P. Tolédano, H. Schmid, M. Clin and J. P. Rivera, Phys. Rev. B, 32, 6006 (1985). T. Ito, N. Morimoto and R. Sadanaga, Acta Cryst., 4, 310 (1951). E. Dowty and J. R. Clark, Z. Kristallographie, 138, 64 (1973). F. Kubel, S. Y. Mao and H. Schmid, Acta Cryst., C48, 1167 (1992). G. Quézel and H. Schmid, Solid State Commun., 6, 447 (1968). M. Clin, J. P. Rivera and H. Schmid, Helv. Phys. Acta., 60, 287 (1987). M. Clin, J. P. Rivera and H. Schmid, Ferroelectrics, 79, 173 (1988). 8a.M. Clin, J. P. Rivera and H. Schmid, Ferroelectrics, 108, 213 (1990). 8b.H. Schmid, Int. J. Magn., 4, 337 (1973) 8c.L. N. Baturov, B. I. Al'shin and D. N. Astrov, Fiz. Tverd. Tela (Leningrad), 19, 916 (1977) [Sov. Phys. Solid State, 19, 534 (1977)]. 9a.L. N. Baturov, N. A. Sokolov and B. I. Al'shin, Fiz. Tverd. Tela (Leningrad), 25, 1994 (1983) [Sov. Phys. Solid State, 25, 1150 (1984)]. 9b.M. E. Mendoza-Alvarez, H. Schmid and J. P. Rivera, Ferroelectrics, 55, 227 (1984). M. Clin, H. Schmid, P. Schobinger and P. Fischer, Phase Transitions, 33, 149 (1991). H. H. Paalman and C. G. Pings, J. Appl. Phys., 33, 2635 (1962). H. M. Rietveld, J. Appl. Cryst., 2, 65 (1969). A. W. Hewat, “Harwell report” AERE-R7350 (1973). V. Scars, Neutron News, 3, 26 (1992). E. Watson and A. J. Freeman, Acta Cryst., 14, 27 (1961). W. Opechowski and R. Guccione, In “Treatise of Magnetism” (Edt. by H. Suhl and G. Rado), Vol. IIA, pp. 105, Academic Press, New York (1965). S. Y. Mao, F. Kubel, H. Schmid, P. Schobinger and P. Fischer, Ferroelectrics, 146, 81 (1993). P. Lacorre, M. Leblanc, J. Pannetier and G. Ferey, J. Magn. Magn. Mat., 94, 337 (1991).ACKNOWLEDGEMENT
REFERENCES