| Transition Temperature | 30 K |
|---|---|
| Experiment Temperature | 8 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P21/n (#14) |
| Magnetic Space Group | P21/c (#14.75) |
| Magnetic Point Group | 2/m (5.1.12) |
| Lattice Parameters | 5.54430 5.59630 7.83030 90.00 90.03 90.00 |
|---|---|
| DOI | 10.1016/s0022-4596(03)00081-1 |
| Reference | P.D. Battle, C.P. Grey, M. Hervieu, C. Martin, C.A. Moore and Y. Paik, Journal of Solid State Chemistry (2003) 175 20-26. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Ru1 | Ru | 1.7 | 0.0 | 1.4 | 2.20 |
Structural chemistry and magnetic properties of La₂LiRuO₆
Peter D. Battle, \( ^{a,*} \) Clare P. Grey, \( ^{b} \) Maryvonne Hervieu, \( ^{c} \) Christine Martin, \( ^{c} \) Caroline A. Moore, \( ^{a} \) and Yonkee Paik \( ^{b} \)
\( ^{a} \) Inorganic Chemistry Laboratory, Oxford University, South Parks Road, Oxford OX1 3QR, UK
\( ^{b} \) Department of Chemistry, State University of New York at Stony Brook, Stony Brook, NY 11794-3400, USA
\( ^{c} \) Laboratoire CRISMAT, UMR 6508 associée au CNRS, ISMRA, 6 Boulevard du Maréchal Juin, 14050 Caen Cedex, France
Received 26 September 2002; received in revised form 1 January 2003; accepted 7 January 2003
Abstract
A combination of magnetometry, electron microscopy, neutron diffraction and \( {}^{7} \) Li MASNMR spectroscopy has been used to determine that \( La_{2}LiRuO_{6} \) has a monoclinic perovskite-related structure (space group \( P2_{1}/n \) , \( a=5.5555(2) \) , \( b=5.5977(2) \) , \( c=7.8454(3) \) Å, \( \beta=90.020(5)^{\circ} \) at 300 K) with a 1:1 ordered arrangement of \( Li^{+} \) and \( Ru^{5+} \) cations occupying the six-coordinate sites. The compound is antiferromagnetic (type I) below 30 K with an ordered magnetic moment of \( 2.2(2)\mu_{B} \) per Ru. The magnetic properties of this phase are compared with those of \( Sr_{3}LiRuO_{6} \) and \( Ca_{3}LiRuO_{6} \) .
© 2003 Elsevier Inc. All rights reserved.
1. Introduction
There has been a recent resurgence of interest in the electronic properties of mixed-metal oxides containing ruthenium, particularly those which adopt perovskite-related crystal structures. Perhaps the most remarkable aspect of this revival is that it has been stimulated by developments in a number of different fields, for example superconductivity \( [1] \) and colossal magnetoresistance \( [2,3] \) . Other recent work has included studies of pseudo-one-dimensional oxides, for example \( Ca_{3.1}Cu_{0.9}RuO_{6} \) and \( A_{3}A^{\prime}RuO_{6} \) (A=Ca, Sr; \( A^{\prime}=Li \) , Na) \( [4,5] \) , by magnetometry and neutron diffraction. Most of the insulating oxides of ruthenium which adopt a magnetically ordered ground state do so below transition temperatures of \( \sim40K \) \( [6,7] \) , and it is therefore surprising that \( Sr_{3}LiRuO_{6} \) and \( Ca_{4}LiRuO_{6} \) order antiferromagnetically at 90 and 120 K, respectively \( [4] \) . Although a full structural study by neutron diffraction has not previously been carried out, magnetic susceptibility measurements on the perovskite-related compound \( La_{2}LiRuO_{6} \) \( [8,9] \) have identified a Néel temperature of 30 K, which is consistent with the behavior of the majority of known ruthenium oxides and therefore inconsistent with the behaviour of \( Sr_{3}LiRuO_{6} \) and \( Ca^{3}LiRuO_{6} \) . In an attempt to identify the characteristics of these two Li/Ru compounds which lead to relatively high Néel temperatures, we have undertaken a comparative study of the structure of \( La_{2}LiRuO_{6} \) by electron diffraction (ED), neutron diffraction and MASNMR spectroscopy. The results of these investigations are described below.
2. Experimental
A polycrystalline sample ( \( \sim6~g~mass \) ) of \( La_{2}LiRuO_{6} \) was prepared using standard ceramic techniques. Stoichiometric quantities of \( La_{2}O_{3} \) and \( RuO_{2} \) were ground together with a 10% excess of \( Li_{2}CO_{3} \) . The loose powder was initially heated at \( 600^{\circ}C \) then, following regrinding, the temperature was increased slowly to \( 700^{\circ}C \) . The reactant mixture was then isostatically pressed into a rod which was heated in air at \( 900^{\circ}C \) , and finally at \( 1000^{\circ}C \) for 12 days. The progress of the reaction was monitored by X-ray powder diffraction and the synthesis was deemed to be complete when further heating produced no change in the diffraction pattern. Samples for transmission electron microscopy were prepared by crushing the bars in n-butanol and the small crystallites in suspension were then deposited onto a holey carbon film, supported by a nickel grid. The ED study was carried out at room temperature with a JEOL
200CX electron microscope, equipped with a KEVEX analyzer. Numerous crystallites were analyzed by energy-dispersive spectroscopy (EDS), allowing the La/Ru ratio to be checked systematically in order to determine the best synthesis conditions (Li is too light to be included in the analysis). The expected La/Ru=2 ratio was confirmed for the sample used for the neutron diffraction study. Neutron powder diffraction experiments were carried out at the LLB (Saclay, France) on the high-resolution diffractometer 3T2 with a wavelength \( \lambda=1.227 \) Å. Data were collected at 8 and 300 K for over the angular range \( 6^{\circ}\leqslant2\theta\leqslant125^{\circ} \) with a stepsize \( \Delta2\theta=0.05^{\circ} \) . The diffractometer G41, working with a wavelength \( \lambda=2.4266 \) Å, was used to determine the temperature evolution of the Bragg scattering. The sample was first cooled down to helium temperature and patterns were then recorded over the angular range \( 17^{\circ}\leqslant2\theta\leqslant97^{\circ} \) whilst warming from 2 K to room temperature. All diffraction data were analyzed using the Rietveld technique [10] as implemented in the GSAS [11] or FULLPROF [12] programs. Peak shapes were described by pseudo-Voigt functions and background levels were fitted by ninth order shifted Chebyshev polynomials. The magnetic behavior of the sample was studied as a function of temperature and applied field using a Quantum Design MPMS 5000 SQUID magnetometer. The magnetization was measured as a function of applied field at 5 K, and as a function of temperature in an applied field of 3 kOe. The latter data were collected during warm-up after cooling the sample in the absence of a field (ZFC) and also while cooling in the measuring field (FC). \( {}^{7} \) Li MASNMR spectra were acquired on a CMX200 spectrometer at an operating frequency of 77.79 MHz for \( {}^{7} \) Li, with a rotor synchronized spin–echo sequence ( \( \pi/2-\tau-\pi-\tau-\alpha cq \) ; \( \tau=1/ \) spinning speed), \( \pi/2 \) s of 2.6 \( \mu \) s and a spinning speed of 21 kHz.
3. Results
The X-ray powder diffraction pattern of the product, collected immediately after the synthesis was complete, was consistent with the presence of only a monoclinic perovskite-related phase, \( La_{2}LiRuO_{6} \) , with an ordered arrangement of Li and Ru cations over the octahedral sites. However, neutron diffraction patterns collected some months after the synthesis showed the presence of a minority second phase, identified as \( \mathrm{La(OH)_{3}} \) ; the concentration of this impurity increased with time. Bright-field electron microscope images showed that the crystallites of \( La_{2}LiRuO_{6} \) are spherical. Reconstruction of the structure in reciprocal space was carried out by tilting crystallites around their crystallographic axes in ED experiments. This resulted in the unit-cell parameters, \( a \approx 5.55 \AA \) ( \( \sim a_{p}\sqrt{2} \) , \( a_{p} \) being the parameter of the perovskite subcell), \( b \approx 5.6 \AA \) ( \( \sim a_{p}\sqrt{2} \) , ) c \approx 7.84 \AA ) ( \( \sim 2a_{p} \) and \( \beta \approx 90^{\circ} \) , with the following conditions limiting the observed reflections: \( h0l: h + l = 2n \) and \( 0k0: k = 2n \) . These data are consistent with the space group \( P2_{1}/n \) . The [001] and [110] ED patterns are presented in Fig. 1. The ED study showed evidence for the systematic appearance of twinning domains in the crystallites. One example is illustrated in Fig. 2; two [110] variants are orientated at \( 90^{\circ} \) , the [110] \( ^{*} \) and [001] \( ^{*} \) directions of the monoclinic cell both being equivalent to the [100] \( _{p} \) directions of the perovskite subcell.
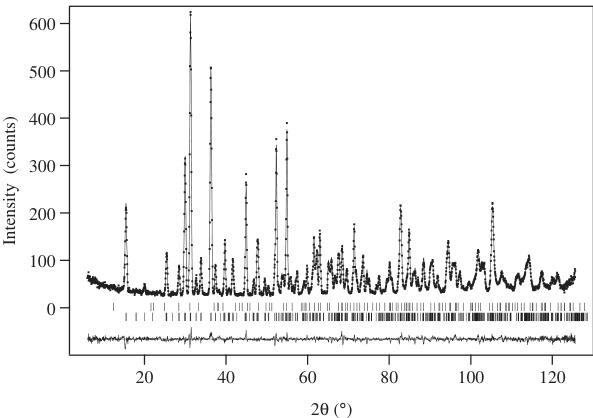
The neutron diffraction data collected on \( La_{2}LiRuO_{6} \) at room temperature were analyzed using space group \( P2_{1}/n \) ; the \( \mathrm{La(OH)_{3}} \) impurity was included as a second phase ( \( \sim1\% \) by weight) in these refinements. The final structural parameters and bond lengths for the principal phase are listed in Tables 1 and 2, respectively. No significant disorder of the Li and Ru cations over the octahedral sites could be detected in trial refinements, and complete cation ordering was assumed during the final stages of the analysis. The thermal motion of all the atoms was assumed to be isotropic. The final observed

Fig. 1. (a) [001] and (b) [110] ED patterns of \( La_{2}LiRuO_{6} \)

Fig. 2. [110] ED pattern of a twinned crystal of La₂LiRuO₆.
Table 1
Structural parameters for \( La_{2}LiRuO_{6} \) at 300 and 8 K
| 300 K | 8 K | ||
| a ( \( \textup{\AA} \) ) | 5.5555(2) | 5.5443(2) | |
| b ( \( \textup{\AA} \) ) | 5.5977(2) | 5.5963(2) | |
| c ( \( \textup{\AA} \) ) | 7.8454(3) | 7.8303(3) | |
| \( \beta \) ( \( ^{\circ} \) ) | 90.020(5) | 90.034(6) | |
| V ( \( \textup{\AA}^{3} \) ) | 243.98(2) | 242.96(2) | |
| La (x, y, z) | x | 0.0075(4) | 0.0083(4) |
| y | 0.9589(2) | 0.9564(2) | |
| z | 0.7494(5) | 0.7491(4) | |
| \( U_{\textup{iso}} \) ( \( \textup{\AA}^{2} \) ) | 0.0051(2) | 0.0000(2) | |
| Li (0.5,0,0) | \( U_{\textup{iso}} \) ( \( \textup{\AA}^2 \) ) | 0.021(2) | 0.018(4) |
| Ru (0.5,0.0,5) | \( U_{\textup{iso}} \) ( \( \textup{\A}^2 \) ) | 0.0056(4) | 0.0013(3) |
| \( \mu_{\textup{xz}}/\mu_{\textup{B}} \) | — | 2.2(2) | |
| O1 (x,y,z) | x | 0.2794(6) | 0.2809(6) |
| y | 0.7041(6) | 0.6993(5) | |
| z | 0.9605(6) | 0.9600(6) | |
| \( U_{\textup{iso}} \) ( \( ^{\textup{\AA}^2} \) ) | 0.0052(7) | 0.0007(7) | |
| O2 (x,y,z) | x | 0.2002(6) | 0.2016(6) |
| y | 0.2174(6) | 0.2212(6) | |
| z | 0.9603(6) | 0.9597(5) | |
| \( U_{\textup{iso}} \) ( \( ^{A^2} \) ) | 0.0075(8) | 0.0019(7) | |
| O3 (x,y,z) | x | 0.9249(4) | 0.9242(4) |
| y | 0.5143(3) | 0.5157(3) | |
| z | 0.7577(4) | 0.7565(4) | |
| \( U_{\textup{iso}} \) (\( \textup{\AA}^2 \) ) | 0.0052(4) | 0.0010(4) | |
| Rwp (%) | 5.07 | 4.86 | |
| \( \chi^2 \) | 2.160 | 2.454 |
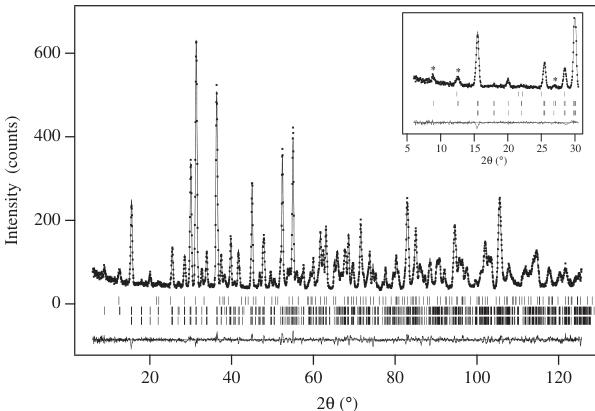
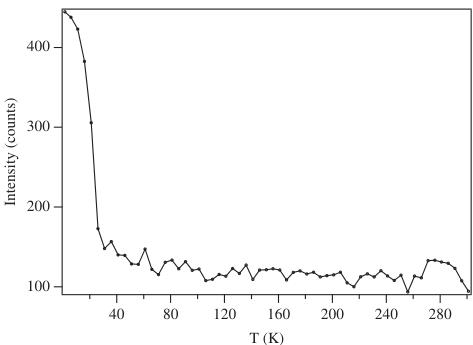
and calculated diffraction patterns are shown in Fig. 3, and the structure is drawn in Fig. 4. The data collected at 8 K contained additional Bragg peaks at low angles that were taken to be magnetic in origin. The angular distribution of these peaks suggested that the magnetic moments of the Ru cations in \( La_{2}LiRuO_{6} \) align to form a type I antiferromagnetic structure at low temperatures. Rietveld refinement of the low-temperature crystal structure (Fig. 5) proceeded smoothly in space group \( P2_{1}/n \) ; there was no evidence to suggest that a structural
Table 2
Bond lengths ( \( \AA \) ) and bond angles (deg) in La \( _{2} \) LiRuO \( _{6} \) at 300 and 8 K
| 300 K | 8 K | |
| La-O1 | 2.656(5) | 2.660(5) |
| 2.450(6) | 2.428(5) | |
| 2.753(6) | 2.733(5) | |
| 3.358(6) | 3.388(5) | |
| La-O2 | 2.444(6) | 2.462(5) |
| 2.678(5) | 2.645(4) | |
| 2.738(6) | 2.747(5) | |
| 3.368(6) | 3.358(5) | |
| La-O3 | 2.532(2) | 2.511(2) |
| 2.423(3) | 2.421(3) | |
| 3.143(2) | 3.165(2) | |
| 3.169(3) | 3.164(3) | |
| Li-O1 | 2.084(3) \( \times \) 2 | 2.099(3) \( \times \) 2 |
| Li-O2 | 2.086(3) \( \times \) 2 | 2.090(3) \( \times \) 2 |
| Li-O3 | 2.066(3) \( \times \) 2 | 2.054(3) \( \times \) 2 |
| Ru-O1 | 1.952(3) \( \times \) 2 | 1.941(3) \( \times \) 2 |
| Ru-O2 | 1.959(3) \( \times \) 2 | 1.945(3) \( \times \) 2 |
| Ru-O3 | 1.948(3) \( \times \) 2 | 1.954(4) \( \times \) 2 |
| O1-Li-O2 | 88.4(2) | 89.7(2) |
| O1-Li-O3 | 90.2(2) | 90.4(2) |
| O2-Li-O3 | 89.6(1) | 89.4(1) |
| O1-Ru-O2 | 89.8(2) | 88.5(2) |
| O1-Ru-O3 | 89.5(2) | 89.4(2) |
| O2-Ru-O3 | 90.0(2) | 90.1(2) |
| Li-O1-Ru | 155.4(3) | 154.3(2) |
| Li-O2-Ru | 154.3(3) | 154.9(2) |
| Li-O3-Ru | 155.6(1) | 155.2(1) |
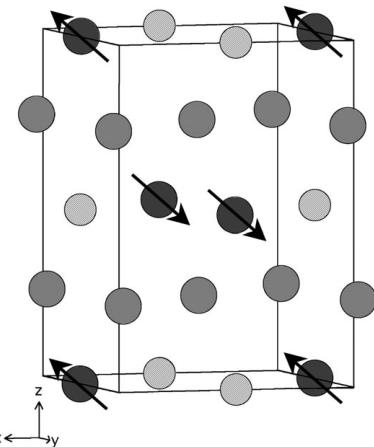
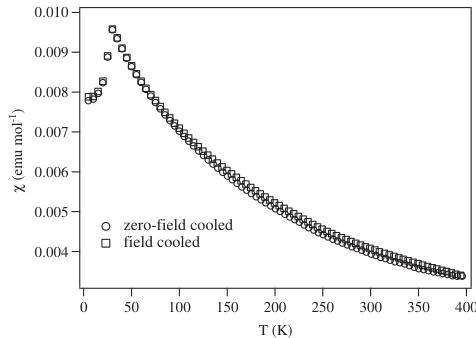
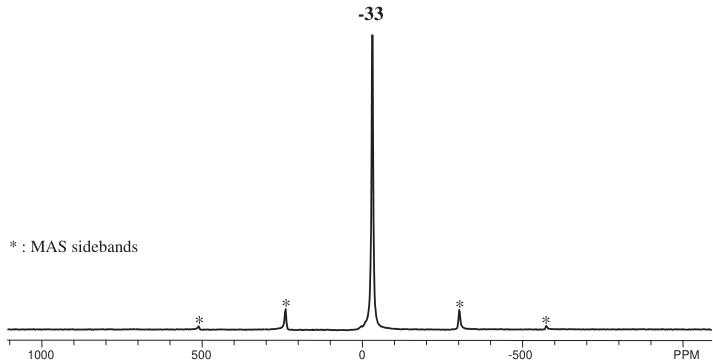
phase transition had occurred on cooling the sample. The ordered component of the Ru magnetic moment was found to lie in the xz plane with components \( m_{x} = 1.7(1) \) , \( m_{z} = 1.4(2) \) \( \mu_{B} \) . The magnetic structure is represented in Fig. 6. The temperature dependence of the magnetic Bragg scattering (Fig. 7) confirmed that the susceptibility maximum observed at 30 K in data from both the present sample (Fig. 8) and that measured previously [9] corresponds to a Néel point. A measurement of \( M(H) \) at 5 K showed no hysteresis. Fitting the high-temperature susceptibility ( \( 100 < T / K < 400 \) ) to the Curie–Weiss law resulted in values of \( \mu_{eff} = 3.90 \mu_{B} \) , \( \theta = -167 K \) . The \( {}^{7}Li \) MAS spectrum of \( La_{2}LiRuO_{6} \) (Fig. 9) shows only one sharp resonance at -33 ppm, indicating that there is only one local environment for Li in this compound. This is consistent with the average structure deduced from the diffraction data; and it is clear that there is a strict alternation of \( RuO_{6} \) and \( LiO_{6} \) octahedra in this double perovskite.
4. Discussion
La₂LiRuO₆ was originally [8,9] described as having an orthorhombic, GdFeO₃-like structure. More recently, following X-ray powder diffraction and EXAFS measurements, Choy et al. [13] recognized that ordering of

Fig. 3. Observed (●) and calculated (−) neutron powder diffraction profiles of \( La_{2}LiRuO_{6} \) at 300 K; a difference curve is plotted. Vertical bars mark reflection positions for the main phase (lower) and the \( \mathrm{La(OH)_{3}} \) impurity (upper).

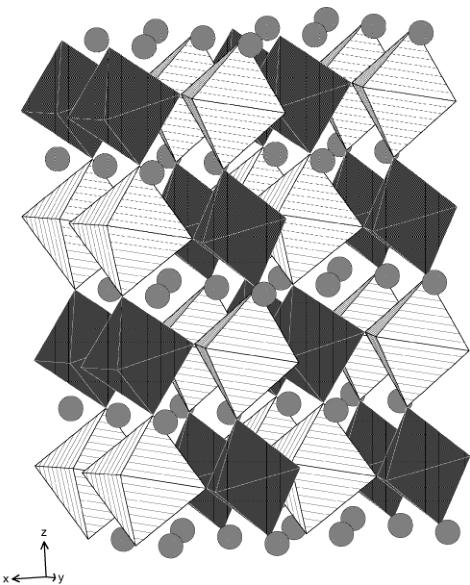
Fig. 4. Crystal structure of \( La_{2}LiRuO_{6} \) ; \( RuO_{6} \) octahedra are shaded, \( LiO_{6} \) octahedra are hatched, circles represent La atoms.
the Li and Ru cations over the six-coordinate sites requires a lowering of the symmetry to monoclinic. The significant difference in both the size and charge of the B-site cations undoubtedly ensures that this ordering is complete in \( La_{2}LiRuO_{6} \) . Our diffraction data show that the three crystallographically distinct Ru–O bond lengths are all very similar to each other, and they are also consistent with the values determined by neutron diffraction in other cubic and pseudo-cubic perovskites. Similarly, the Li–O distances lie within a narrow range and are typical of \( Li^{+} \) in six-coordination. The results of the present study have a precision which is an order of magnitude higher than that of the previous X-ray work, and they show that Choy et al. underestimated the mean Ru–O distance and overestimated the mean Li–O distance. Interestingly, the mean Ru–O distance is closer to that determined using EXAFS than to that determined by X-ray powder diffraction. Unfortunately, our results call into question the close correlation between Ru–O bond length and the crystal-field splitting ( \( \Delta \) ) of the Ru d orbitals which was proposed by Choy et al. on the basis of XANES and X-ray diffraction data collected on a series of Ru perovskites. The O–Ru/Li–O bond angles in \( La_{2}LiRuO_{6} \) do not deviate from \( 90^{\circ} \) by more than \( 0.6^{\circ} \) , and the structure can, like many other perovskites, be considered to consist of a network of regular, vertex-sharing octahedra. The deviation from the ideal cubic symmetry is introduced by the nonlinearity of the Li–O–Ru linkages, that is by the relative rotation of neighboring octahedra. The degree of rotation in this compound (Table 2) is large compared to that in, for example, \( Sr_{2}YRuO_{6} \) and \( Sr_{2}LuRuO_{6} \) (Y/Lu–O–Ru \( \sim 158-161^{\circ} \) ) but small compared to that in (CaLa)CaRuO \( _{6} \) (Ca–O–Ru \( \sim 145^{\circ} \) ). The atomic density is approximately 10% higher in \( La_{2}LiRuO_{6} \) than in any of these other compounds, a fact which can be ascribed to the presence of the relatively small Li \( ^{+} \) cation. These structural characteristics will be referred to in the discussion of the magnetic properties below.
Comparison of the MASNMR data with the results of the crystallographic study reinforces the idea that it may be possible to establish a useful correlation between

Fig. 5. Observed (●) and calculated (—) neutron powder diffraction profiles of \( La_{2}LiRuO_{6} \) at 8 K; a difference curve is plotted. Vertical bars mark reflection positions for nuclear scattering from the main phase (lower), magnetic scattering (center) and the \( \mathrm{La(OH)_{3}} \) impurity (upper). Strong magnetic reflections are labeled ( \( ^{*} \) ) in the inset.

Fig. 6. Magnetic structure of \( La_{2}LiRuO_{6} \) ; arrowed circles represent Ru, hatched circles Li, and shaded circles La.
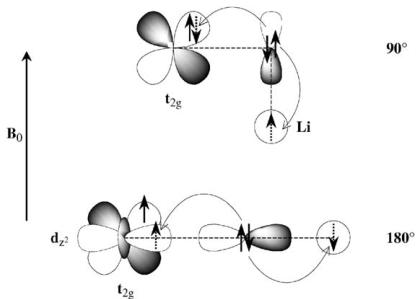
\( ^{7} \) Li NMR shifts and Li- \( \hat{O} \) -M bond angles. The NMR shift observed in \( La_{2}LiRuO_{6} \) is ascribed to a hyperfine interaction, involving transfer of unpaired spin density from \( Ru^{5+} \) to the 2s Li orbital, via the intervening oxygen atoms. The \( Ru^{5+} \) ion \( (4d^{3}; t_{2g}^{3}) \) is isoelectronic with \( Mn^{4+} \) \( (3d^{3}) \) , and it is therefore reasonable to propose shift mechanisms for the ruthenates which are similar to those used to rationalize the shifts seen in a series of Mn(IV) compounds [14, 15]. Two mechanisms are important: the first involves an interaction between the \( (\mathrm{Mn}/\mathrm{Ru}) t_{2g} \) orbitals, the \( 2p_{\pi} \) orbital on the directly bound oxygen and the Li 2s orbital (the \( 90^{\circ} \) interaction).

Fig. 7. Temperature dependence of the intensity of the 001 magnetic reflection of \( La_{2}LiRuO_{6} \) .

Fig. 8. Molar magnetic susceptibility (ZFC and FC) of \( La_{2}LiRuO_{6} \) as a function of temperature.

Fig. 9. Magic angle spinning \( {}^{7} \) Li NMR spectrum of La \( _{2} \) LiRuO \( _{6} \) acquired with a spinning speed of 21 kHz.

Fig. 10. Schematic diagrams of transferred hyperfine interactions via \( 90^{\circ} \) and \( 180^{\circ} \) Ru–O–Li bonds, showing how the different pathways put spin density of opposite sign in the Li 2s orbital.
(Fig. 10). The second interaction (the \( 180^{\circ} \) interaction) involves an overlap between the empty (Mn/Ru) \( e_{g} \) orbitals, an oxygen \( 2p_{\sigma} \) orbital and the Li 2s orbital. For \( Mn^{4+} \) these interactions result in hyperfine shifts of between 250 and 300 ppm, and -75 and -125 ppm, respectively, depending on the structure type. For example, for \( \mathrm{La}_{2}(\mathrm{Li}_{0.5}\mathrm{Mn}_{0.5})\mathrm{O}_{4} \) [16], which adopts the \( K_{2}NiF_{4} \) structure, with strict alternation of Li and Mn within the perovskite layers, a shift of approx. -500 ppm was observed and attributed to the presence of four Li–O–Mn \( 180^{\circ} \) interactions. The Li local environment in \( La_{2}LiRuO_{6} \) comprises six Li–O–Ru interactions, which in the ideal, undistorted perovskite, should be linear ( \( 180^{\circ} \) ). Thus a large negative shift is predicted for the undistorted material. The much smaller observed shift of -33 ppm is consistent with the large tilting of the octahedra, resulting in Li–O–Ru bond angles of between 154.3(3) and 155.6(1), and reflects contributions from the two competing mechanisms. A decrease from \( 180^{\circ} \) to \( 155^{\circ} \) will result in a decrease in the overlap between the O 2p orbital and the Li 2s orbital, resulting in a decrease in the size of the “ \( 180^{\circ} \) interaction”. Concomitantly, the contribution from the positive \( 90^{\circ} \) interaction will increase, further decreasing the magnitude of the negative shift. Experiments designed to establish a more quantitative \( \delta \) :bond–angle relationship for mixed Li/Ru oxides are in progress.
The effective magnetic moment of \( Ru^{5+} \) in the paramagnetic phase of \( La_{2}LiRuO_{6} \) is comparable to the spin-only value ( \( 3.87 \mu_{B} \) ) calculated for a \( d^{3} \) cation, and smaller than the values ( \( \geqslant 4 \mu_{B} \) ) measured in many compounds [6,17], for example \( Ba_{2}LaRuO_{6} \) and \( (\mathrm{CaLa})\mathrm{CaRuO}_{6} \) ; it is, however, larger than the value of \( 3.13 \mu_{B} \) observed in \( Sr_{2}YRuO_{6} \) [7]. The high effective magnetic moments and the large value of the ratio \( \theta / T_{\mathrm{N}} (>10) \) observed in the compounds exemplified by \( Ba_{2}LaRuO_{6} \) and \( (\mathrm{CaLa})\mathrm{CaRuO}_{6} \) lead us to describe their outer d electrons as itinerant, albeit strongly correlated. The reduced moment and the relatively low value of \( \theta / T_{\mathrm{N}} \) (5.5) of \( Sr_{2}YRuO_{6} \) prompted us to suggest that the 4d electron system in this compound should be regarded as localized, although the low value of the ordered cation moment ( \( 1.85 \mu_{B} \) ) in the low-temperature phase caused us to add a note of caution. In \( La_{2}LiRuO_{6} \) , we find a modest effective magnetic moment, \( \theta / T_{\mathrm{N}} = 5.5 \) , and an ordered moment of \( 2.2 \mu_{B} \) per Ru, the largest value observed in a \( Ru^{5+} \) perovskite. We are therefore confident that the outer electrons in this compound lie in the localized region of the conceptual temperature—transfer-integral phase diagram originally drawn by Goodenough [18]. This requires that the degree of involvement of the \( Ru^{5+} \) cation in covalent interactions is relatively low, a condition that is consistent with the presence of a high concentration of acidic \( La^{3+} \) cations which compete effectively for the available electron density. The type I magnetic structure adopted by \( La_{2}LiRuO_{6} \) is the same as that found in \( (\mathrm{CaLa})\mathrm{CaRuO}_{6} \) and \( Sr_{2}YRuO_{6} \) , and
\( Ba_{2}LaRuO_{6} \) thus remains the only member of this group of compounds in which the next-nearest-neighbor interactions are strong enough to be competitive with those between nearest neighbors, thus causing the adoption of a Type IIIa structure. The diamagnetic, six-coordinate cations (B=Ca, Y, or Li) in the other compounds do not have energetically accessible orbitals (2p in the case of Li) which can take part in a Ru–O–B–O–Ru superexchange mechanism (the \( d^{3} \) electron configuration of \( Ru^{5+} \) dictates that this interaction can only occur through \( \pi \) orbitals).
We now turn to a comparison of the magnetic properties of \( La_{2}LiRuO_{6} \) with those of pseudo-1D \( Ca_{3}LiRuO_{6} \) and \( Sr_{3}LiRuO_{6} \) ; all of these compounds show antiferromagnetic ordering in a localized electron system at low temperatures. The \( RuO_{6} \) octahedra are essentially the same size in all three compounds, and arguments based on the local coordination geometry around Ru cannot be used to account for the relatively low Néel temperature of \( La_{2}LiRuO_{6} \) . Furthermore, the trigonal prismatic coordination of Li in the latter compounds leads to a mean Li–O bond length of \( \sim2.2\AA \) , significantly longer than that in \( La_{2}LiRuO_{6} \) , and the interchain superexchange pathways (which do not involve the Li sites) are also long compared to the dominant nearest-neighbor pathway in the perovskite. It is therefore difficult to rationalize the high \( T_{N} \) of \( Ca_{3}LiRuO_{6} \) and \( Sr_{2}LiRuO_{6} \) simply in terms of the structural chemistry. If, as discussed above, the relatively large ordered magnetic moment associated with \( Ru^{5+} \) in \( La_{2}LiRuO_{6} \) is taken as an indication that the covalency in the \( RuO_{6} \) octahedra is lower than that in the pseudo-1D compounds, then it could be argued that the latter should have higher ordering temperatures. This hypothesis effectively identifies the acid/base characteristics of the non-magnetic cations as the key parameter whilst ignoring many others, for example the strength of the superexchange interactions should increase with the number density of Ru cations, which is \( \sim20\% \) higher in \( La_{2}LiRuO_{6} \) than in \( Sr_{3}LiRuO_{6} \) . These competing factors will all influence the magnetic ordering temperatures, but they do not give a clear prediction as to which compound will have the higher \( T_{N} \) . We believe the most significant clue to the reason for the higher ordering temperatures in the pseudo-1D compounds comes from a consideration of the temperatures \( \theta \) and \( T_{N} \) . The former is a measure of all the interionic magnetic interactions in the material, whereas the latter reflects the strength of those which are compatible with the spin structure adopted in the ordered state. The values of \( \theta \) for \( Sr_{3}LiRuO_{6} \) and \( La_{2}LiRuO_{6} \) are essentially the same ( \( -165\ K \) [4]), suggesting that the strength of magnetic coupling is approximately the same in the two compounds. The difference in ordering temperatures then comes about because each \( Ru^{5+} \) cation in the former is antiferromagnetically coupled to all of the nearest-neighbor \( Ru^{5+} \) cations, whereas the transition metal cations in the latter are antiferromagnetically coupled to eight neighbors, and ferromagnetically to four others. We therefore believe that the frustration inherent in a pseudo-fcc structure is the most significant factor in determining the ordering temperature of \( La_{2}LiRuO_{6} \) , and that an ordering temperature of \( \sim100\ K \) , as in \( Sr_{3}LiRuO_{6} \) , is a better indication of the inherent strength of the superexchange interactions between Ru cations in an insulating perovskite-related material.
Acknowledgments
We thank EPSRC for the award of a studentship to CAM, NATO for the award of a Fellowship to CM, Dr. F. Bourée (3T2) and Dr. G. André (G41) for experimental assistance at Saclay.
References
[1] Y. Maeno, H. Hashimoto, K. Yoshida, S. Nishizaki, T. Fujita, J.G. Bednorz, F. Lichtenberg, Nature 372 (1994) 532.
[2] C. Martin, A. Maignan, M. Hervieu, B. Raveau, J. Hejtmanek, Eur. Phys. J. B 16 (2000) 469.
[3] B. Raveau, A. Maignan, C. Martin, R. Mahendiran, M. Hervieu, J. Solid State Chem. 151 (2000) 330.
[4] J. Darriet, F. Grasset, P.D. Battle, Mater. Res. Bull. 32 (1997) 139.
[5] P.D. Battle, G.R. Blake, J.C. Burley, E.J. Cussen, J. Sloan, J.F. Vente, J. Darriet, F. Weill, MRS Symp. Proc. 547 (1999) 45.
[6] P.D. Battle, J.B. Goodenough, R. Price, J. Solid State Chem. 46 (1983) 234.
[7] P.D. Battle, W.J. Macklin, J. Solid State Chem. 52 (1984) 138.
[8] E.O. Oh-Kim, G. Demazeau, P. Hagenmuller, Rev. Chim. Minér. 24 (1987) 613.
[9] K. Hayashi, G. Demazeau, M. Pouchard, C.R. Acad. Sci. Paris t.292 (1981) 1433.
[10] H.M. Rietveld, J. Appl. Crystallogr. 2 (1969) 65.
[11] A.C. Larson, R.B. von-Dreele, General Structure Analysis System (GSAS), Los Alamos National Laboratories, Report LAUR 86-748, 1990.
[12] J. Rodriquez-Caravajal, FULLPROF, LLB Saclay, France, 1995.
[13] J.H. Choy, J.Y. Kim, S.H. Hwang, S.J. Kim, G. Demazeau, Int. J. Inorg. Mater. 2 (2000) 61.
[14] Y.J. Lee, F. Wang, C.P. Grey, J. Am. Chem. Soc. 120 (1998) 12601.
[15] C. Pan, Y.J. Lee, B. Ammundsen, C.P. Grey, Chem. Mater. 14 (2002) 2289.
[16] J.C. Burley, P.D. Battle, D.J. Gallon, J. Sloan, C.P. Grey, M.J. Rosseinsky, J. Am. Chem. Soc. 124 (2002) 620.
[17] P.D. Battle, C.W. Jones, J. Solid State Chem. 78 (1989) 108.
[18] J.B. Goodenough, Prog. Solid State Chem. 5 (1971) 145.