| Transition Temperature | 39 K |
|---|---|
| Experiment Temperature | 2 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | P63/mmc (#194) |
| Magnetic Space Group | Cm'c'm (#63.462) |
| Magnetic Point Group | m'm'm (8.4.27) |
| Lattice Parameters | 8.85980 8.85980 9.61680 90.00 90.00 120.00 |
|---|---|
| DOI | 10.1103/physrevb.93.024407 |
| Reference | D.I. Gorbunov, M.S. Henriques, A.V. Andreev, V. Eigner, A. Gukasov, X. Fabreges, Y. Skourski, V. Petricek and J. Wosnitza, Physical Review B (2016) 93. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Nd1_1 | Nd | 0.0 | 0.0 | 0.95 | 0.95 |
| Nd1_2 | Nd | 0.0 | 0.0 | 2.66 | 2.66 |
Magnetic anisotropy and reduced neodymium magnetic moments in Nd_{3}Ru_{4}Al_{12}
D. I. Gorbunov, \( ^{1,2,*} \) M. S. Henriques, \( ^{2,3} \) A. V. Andreev, \( ^{2} \) V. Eigner, \( ^{2} \) A. Gukasov, \( ^{4} \) X. Fabrèges, \( ^{4} \) Y. Skourski, \( ^{1} \) V. Petriček, \( ^{2} \) and J. Wosnitza \( ^{1,5} \)
\( ^{1} \) Dresden High Magnetic Field Laboratory (HLD-EMFL), Helmholtz-Zentrum Dresden-Rossendorf, D-01314 Dresden, Germany
\( ^{2} \) Institute of Physics, Czech Academy of Sciences, Na Slovance 2, 182 21 Prague, Czech Republic
\( ^{3} \) CCTN, IST, University of Lisbon, Nuclear and Technological Campus, P-2695-066 Bobadela, Portugal
\( ^{4} \) Laboratoire Léon Brillouin, CE de Saclay, DSM/IRAMIS, F-91191 Gif-sur-Yvette, France
\( ^{5} \) Institut für Festkörperphysik, TU Dresden, D-01062 Dresden, Germany
(Received 11 October 2015; revised manuscript received 16 December 2015; published 12 January 2016)
This paper addresses the electronic properties of \( Nd_{3}Ru_{4}Al_{12} \) (hexagonal crystal structure) with focus on its magnetic anisotropy that allows a comparison between single-ion and two-ion mechanisms when comparing to \( U_{3}Ru_{4}Al_{12} \) . We performed magnetization measurements on a single crystal in static and pulsed magnetic fields as well as neutron-diffraction experiments. \( Nd_{3}Ru_{4}Al_{12} \) is a strongly anisotropic uniaxial ferromagnet with a Curie temperature of 39 K. The magnetic moments are aligned collinearly along the [001] axis. The magnetic structure of \( Nd_{3}Ru_{4}Al_{12} \) has orthorhombic symmetry for which the crystallographic Nd site is split into two magnetically inequivalent positions, Nd1 and Nd2. The Nd1 and Nd2 atoms exhibit reduced magnetic moments, 0.95 and \( 2.66 \mu_{B} \) , as compared to the free \( Nd^{3+} \) -ion value ( \( 3.28 \mu_{B} \) ). We discuss this finding in terms of crystal-field effects and competing exchange and anisotropy interactions. Since the single-ion mechanism in \( Nd_{3}Ru_{4}Al_{12} \) leads to uniaxial anisotropy and the two-ion mechanism of the actinide analog \( U_{3}Ru_{4}Al_{12} \) is known to lead to planar anisotropy, this paper demonstrates the decisive influence of these different mechanisms on the magnetic anisotropy.
DOI: 10.1103/PhysRevB.93.024407
I. INTRODUCTION
The anisotropy of a magnetic system is reflected in the preference of the magnetization to be oriented along a specific crystallographic direction. The microscopic origin of the magnetic anisotropy lies in the existence of nonquenched orbital moments. For a given atom, the orbital moment is locked in by the crystal lattice, whereby the spin moment due to spin-orbit interaction also favors a particular orientation \( [1] \) . The intrinsic magnetic anisotropy may have several contributions, including dipolar interactions, single-ion and two-ion anisotropy, quadrupolar interactions, and anisotropic exchange \( [2] \) . For a vast majority of 4f- and 5f-based intermetallic compounds, one may single out the two predominant sources of anisotropy, single-ion and two-ion contributions \( [3–6] \) .
The single-ion mechanism is due to the electrostatic interaction between the crystalline electric field and the aspherical charge cloud of the magnetic electrons. The electronic orbital adopts an orientation in the crystal lattice that minimizes its interaction with the potential created at the atomic site by the rest of the crystal. The main parameters that determine the type and strength of the anisotropy are the shape of the electronic charge cloud and the nature of the crystalline electric field \( [5,7] \) . The single-ion anisotropy is most often encountered in intermetallic compounds based on rare-earth elements, most of which have well-localized 4f-electronic shells \( [8–10] \) . It is the major source of anisotropy in hard ferromagnetic materials, some of which \( \left(\mathrm{SmCo}_{5}, \mathrm{Nd}_{2}\mathrm{Fe}_{14}\mathrm{B}\right) \) are high-performance permanent magnets \( [11–15] \) .
The two-ion anisotropy is inherent to intermetallic compounds based on early actinides (up to plutonium) that have more extended 5f wave functions compared to the 4f elements. The 5f electrons are partly delocalized due to their participation in bonding \( [16–19] \) . The directional character of the hybridization of the 5f states is the origin of the two-ion anisotropy. As a consequence, strong magnetocrystalline anisotropy is observed in a majority of intermetallic compounds based on early actinides that exhibit a 5f contribution to the magnetic moments and is not restricted to magnetically ordered materials \( [20–27] \) .
Although several studies have addressed the relative importance of the single-ion and two-ion anisotropy terms in a given system \( [3,4,28,29] \) , a straightforward comparison between the anisotropy mechanisms is still lacking. A possible way for such a comparison seems to be direct investigation of 4f and 5f analogs, i.e., elements having the same number of electrons in their f shells, placed in the same atomic environment. It is also preferable that a long-range magnetic order originates from the f elements alone so that other potentially magnetic species contribute negligibly to the anisotropy and do not hamper the analysis. Since the single-ion and two-ion mechanisms have different origins, the corresponding compounds should display magnetic anisotropies of different types.
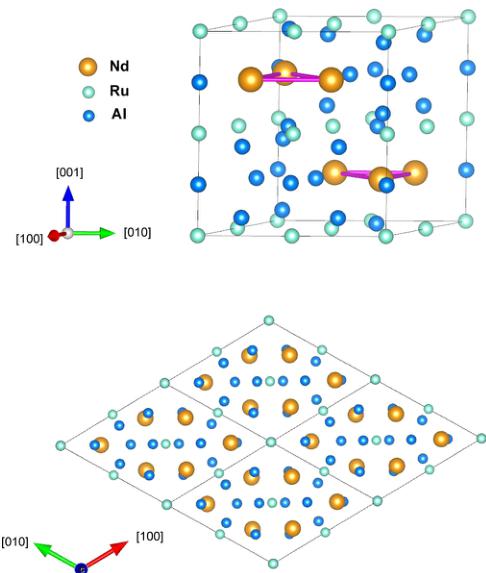
\( R_{3}Ru_{4}Al_{12} \) compounds (R is a rare-earth element or uranium) are excellent candidates for such a study. They crystallize in the hexagonal \( Gd_{3}Ru_{4}Al_{12} \) -type crystal structure (space group \( P6_{3}/mmc \) , two formula units per elementary cell). In the unit cell, two types of layers can be distinguished (upper panel in Fig. 1). The layers containing the R and Al atoms are planar, whereas those containing the Ru and Al atoms are slightly corrugated (a detailed description of the crystal structure can be found in Refs. [30–32]). The R atoms occupy one crystallographic position and form triangular nets parallel to the \( (ab) \) plane (lower panel in Fig. 1). Until now, the only reported compound based on a

FIG. 1. Hexagonal crystal structure \( (P6_{3}/mmc) \) of \( Nd_{3}Ru_{4}Al_{12} \) : view of the unit cell (upper panel) and projection onto the \( (ab) \) plane (lower panel). The unit cell is indicated by the dark lines, the pink (thick) lines show the triangles formed by the Nd atoms.
5f element has been \( U_{3}Ru_{4}Al_{12} \) [33,34]. Since the electronic configuration of uranium is \( 5f^{3} \) , its analog among the light lanthanides is neodymium, having the \( 4f^{3} \) structure. Both, the \( Nd_{3}Ru_{4}Al_{12} \) and \( U_{3}Ru_{4}Al_{12} \) compounds display long-range magnetic order that originates from the Nd and U atoms, respectively [33–36]. The neodymium-based compound is a ferromagnet, while its uranium analog is an antiferromagnet. So far, only \( Nd_{3}Ru_{4}Al_{12} \) polycrystals have been studied, and relatively scarce information on the electronic properties is available [35,36]. For \( U_{3}Ru_{4}Al_{12} \) , single-crystal neutron diffraction revealed a noncollinear magnetic structure with the U moments confined to the basal plane.
In this paper, we report on the electronic properties obtained on a \( Nd_{3}Ru_{4}Al_{12} \) single crystal. We find that \( Nd_{3}Ru_{4}Al_{12} \) exhibits a collinear ferromagnetic order with the magnetic moments aligned along the [001] axis. Thus, the uniaxial anisotropy of \( Nd_{3}Ru_{4}Al_{12} \) contrasts with the planar anisotropy of \( U_{3}Ru_{4}Al_{12} \) . Unexpectedly, from our magnetization and neutron-diffraction data, we obtain that two-thirds of the Nd magnetic moments are reduced by 20%, and the remaining one-third by as much as 70% as compared to the free \( Nd^{3+} \) -ion value, \( 3.28 \mu_{B} \) . We attribute this finding to crystal-field effects and competing exchange and anisotropy interactions. We conclude that, despite different hybridization strengths, crystal-field effects, and types of magnetic order, the single-ion and two-ion anisotropies are two distinct mechanisms that can clearly be distinguished in 4f- and 5f-based intermetallic compounds.
II. EXPERIMENTAL DETAILS
A single crystal of \( Nd_{3}Ru_{4}Al_{12} \) was grown by a modified Czochralski method in a triarc furnace from a quasistoichiometric mixture of the pure elements (99.9% Nd, 99.99% Ru, and 99.999% Al) with an Al mass excess of 1%. The resulting single crystal was cylinder shaped with a height of 20 mm and a diameter of 5 mm. The crystal structure was determined on a piece of the single crystal crushed into fine powder. The lattice parameters of the hexagonal unit cell, \( a = 8.862(1) \) Å and \( c = 9.627(1) \) Å, are in good agreement with those reported previously on polycrystalline samples [35,36]. Back-scattered Laue patterns were used to check the single-crystalline state and to orient the samples along the principal crystallographic directions for magnetization and electrical-resistivity measurements as well as for a neutron-diffraction study.
In order to check the structural details of \( Nd_{3}Ru_{4}Al_{12} \) , single crystal x-ray diffraction was undertaken on a small crystal piece of dimensions \( 0.28 \times 0.25 \times 0.16 \, mm^{3} \) glued on the top of a glass fiber and mounted onto a goniometer head. The diffracted intensities were collected at ambient temperature using a four-circle diffractometer (Gemini of Agilent) equipped with a Mo x-ray tube \( [\lambda(\mathrm{MoK}_{\alpha}) = 0.71073 \, \text{\AA}] \) , Mo-enhance collimator, graphite monochromator, and an Atlas CCD detector. The CrysAlis [37] software was used to collect and process the data and to face index the crystal shape, necessary to perform the accurate absorption correction in combination with a Gaussian correction based on spherical harmonic functions. The Superflip [38] program was used for structure solution and the Jana2006 package [39] for structure refinement. The refinement confirmed the correctness of the structural model with R-factor converging to \( R_{obs} = 2.17\% \) . The lattice parameters obtained from the single-crystal x-ray diffraction are \( a = 8.8598(5) \, \AA \) and \( c = 9.6168(5) \, \AA \) , in good agreement with those determined from powder diffraction. The refined atomic positions and equivalent isotropic displacement parameters are given in Table I.
The temperature and field dependences of the magnetization were measured along the principal crystallographic directions using a Physical Property Measurement System PPMS-14 (Quantum Design) in static fields up to 14 T between 2 and 300 K. The specific heat was measured by use of the relaxation method in the PPMS. The temperature dependence of the electrical resistivity was measured by the four-point method with excitation current of I = 1 mA flowing along the [120] axis.
The magnetization in pulsed magnetic fields (pulse duration 20 ms) up to 57 T was measured at the Dresden High Magnetic Field Laboratory. The high-field magnetometer used for the measurements is described in detail in Ref. [40]. Absolute values of the magnetization were calibrated using data obtained in static magnetic fields.
A single-crystal neutron-diffraction study was carried out using the two-axis diffractometer Super-6T2 ( \( \lambda = 0.902 \) Å) of the Laboratoire Léon Brillouin, Saclay, France [41]. Neutron-scattering intensity maps were first recorded at 2 and 50 K by use of a position-sensitive detector (PSD) rotating the sample around its vertical axis with steps of \( 0.1^{\circ} \) . This enables exploring large three-dimensional segments of the reciprocal
TABLE I. Refined atomic coordinates \( (x, y, z) \) , equivalent isotropic displacement parameters \( (U_{\mathrm{eq}}) \) , and their estimated standard deviations for \( Nd_{3}Ru_{4}Al_{12} \) .
| Atom | Wyckoff position | x | y | z | Ueq(Å2) |
| Nd | 6h | 0.19165(3) | 0.38329(7) | 1/4 | 0.0048(2) |
| Ru1 | 2a | 0 | 0 | 0 | 0.0029(3) |
| Ru2 | 6g | 1/2 | 1/2 | 0 | 0.0036(3) |
| Al1 | 6h | 0.56159(1) | 0.43841(1) | 1/4 | 0.0045(5) |
| Al2 | 12k | 0.32462(3) | 0.16231(1) | 0.0754(2) | 0.0049(4) |
| Al3 | 4f | 1/3 | 2/3 | 0.00866(3) | 0.0052(7) |
| Al4 | 2b | 0 | 0 | 1/4 | 0.0064(9) |
space by converting a complete set of PSD images to the crystal reciprocal space. Next, the configuration was changed to use a single lifting counter to collect more extensive datasets: 230 reflections at 50 K and 572 reflections at 2 K. The resulting data were analyzed using the Jana2006 [39] program. For the refinements of the magnetic moments, we used the magnetic form factor of the \( Nd^{3+} \) ion of the form \( \langle j_{0}\rangle + c_{2}\langle j_{2}\rangle \) , according to the dipolar approximation, where \( \langle j_{0}\rangle \) and \( \langle j_{2}\rangle \) are the radial integrals calculated for the \( Nd^{3+} \) ion and the constant \( c_{2} \) is the ratio between the orbital and the total magnetic moment of \( Nd^{3+} \) .
III. RESULTS
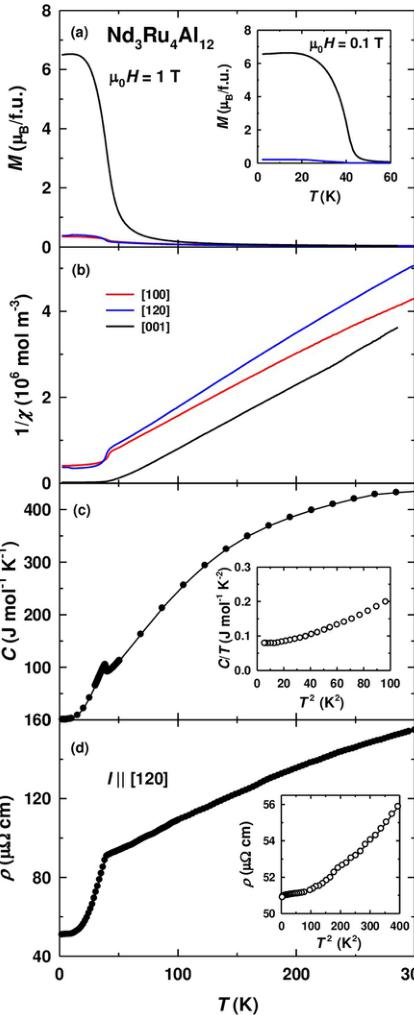
Figure 2(a) shows the temperature dependences of the magnetization, M, measured in a field of 1 T aligned along the [100], [120], and [001] axes of the \( Nd_{3}Ru_{4}Al_{12} \) single crystal. Below 100 K, a pronounced anisotropy is observed for fields applied in the basal plane and along the [001] axis. The increase of the M values with decreasing temperature is related to the onset of magnetic order. The magnetization grows most strongly for the field aligned along the [001] axis. The shape of this curve is reminiscent of a ferromagnetic type of order. However, at the lowest temperatures the magnetization slightly decreases, as a result of which it displays a weak maximum at around 10 K. The maximum is also seen in the lower field of 0.1 T [inset in Fig. 2(a)]. This effect was not observed in polycrystalline samples [36].
From the magnetization data in 1 I, we calculated the static inverse susceptibility, \( 1/\chi \) [Fig. 2(b)]. At high temperatures, \( \chi \) follows the modified Curie-Weiss law
\[ \chi=\frac{C_{\mathrm{CW}}}{T-\theta}+\chi_{0}, \quad (1) \]
where \( C_{CW} \) is the Curie constant, proportional to the effective magnetic moment, \( \theta \) is the Weiss temperature, and \( \chi_{0} \) is a temperature-independent term. Table II indicates that the effective magnetic moment per Nd atom, \( \mu_{eff} \) , is not far from the expected value, \( g_{J}\sqrt{J(J+1)} = 3.62 \mu_{B} \) ( \( g_{J} = 8/11 \) is the Landé factor of Nd, and \( J = 9/2 \) is the quantum number of the total Nd momentum). The Weiss temperature is close to 0 K for field applied in the basal plane and is about 45 K for field along [001]. \( \chi_{0} \) was found to be of the order of \( 1 \times 10^{-8} m^{3} mol^{-1} \) for field along the basal-plane directions and zero along the [001] axis.
The phase transition into the magnetically ordered state is seen as a \( \lambda \) -type anomaly in the specific heat, C [Fig. 1(c)]. From this anomaly, we extract the Curie temperature of \( T_{C} = 39 \) K in \( Nd_{3}Ru_{4}Al_{12} \) . This agrees with the magnetization in 0.1 T that strongly increases around 40 K [see inset in Fig. 2(a)]. For the polycrystalline samples, \( T_{C} = 40 \) K was reported [35,36]. Plotting the specific heat as \( C/T \) vs \( T^{2} \) , we obtain a low-temperature C/T ratio of approximately 80 mJ mol \( ^{-1} \) K \( ^{-2} \) [inset in Fig. 2(c)]. Since a pronounced magnetic contribution to the specific heat is expected to be present at low temperatures, this value is different from the Sommerfeld coefficient related to the density of states of itinerant electrons at the Fermi level. For the same reason, these data do not allow us to determine the Debye temperature, \( \Theta_{D} \) , of the compound. It can be estimated using \( \Theta_{D} \) and the molar mass, m, of the isostructural nonmagnetic compound \( Y_{3}Ru_{4}Al_{12} \) (a = 8.783 Å and c = 9.534 Å, Ref. [42])
\[ \frac{\Theta_{\mathrm{D}}(\mathrm{Nd}_{3}\mathrm{Ru}_{4}\mathrm{Al}_{12})}{\Theta_{\mathrm{D}}(\mathrm{Y}_{3}\mathrm{Ru}_{4}\mathrm{Al}_{12})}=\left(\frac{m(\mathrm{Y}_{3}\mathrm{Ru}_{4}\mathrm{Al}_{12})}{m(\mathrm{Nd}_{3}\mathrm{Ru}_{4}\mathrm{Al}_{12})}\right)^{\frac{1}{3}}. \quad (2) \]
Using \(\Theta_{\mathrm{D}} = 476 \mathrm{~K}\) for \(Y_{3}\mathrm{Ru}_{4}\mathrm{Al}_{12}\), we arrive at \(\Theta_{\mathrm{D}} = 452 \mathrm{~K}\) for \(\mathrm{Nd}_{3}\mathrm{Ru}_{4}\mathrm{Al}_{12}\).
The electrical resistivity, \( \rho \) , decreases steeply below 40 K when entering the ferromagnetic state [Fig. 2(d)]. At low temperatures, the resistivity approaches the residual value, \( \rho_{0} = 51 \mu\Omega cm \) . When plotting \( \rho \) vs \( T^{2} \) at low temperatures [inset of Fig. 2(d)] it becomes clear that, apart from electron-electron scattering ( \( \propto T^{2} \) ), an additional mechanism, most likely electron-magnon scattering, contributes to the resistivity.
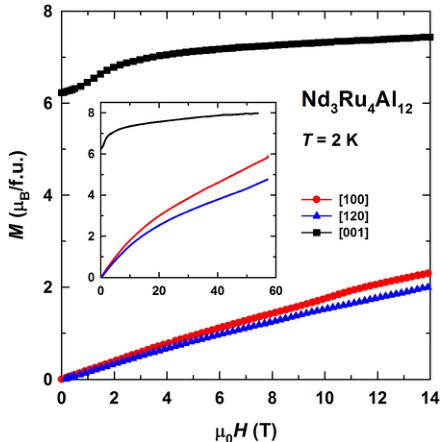
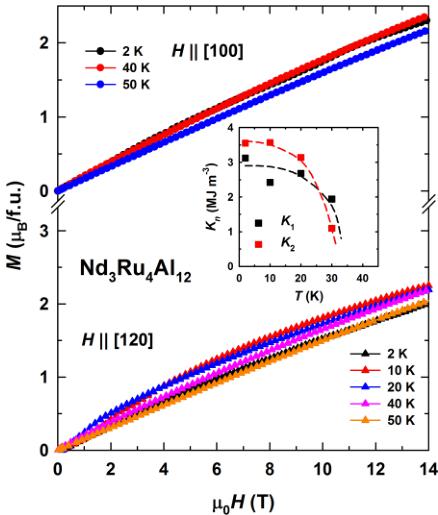
Figure 3 shows the field-dependent magnetization along the principal crystallographic directions of \( Nd_{3}Ru_{4}Al_{12} \) at 2 K in fields up to 14 T (only data for decreasing field are shown, the hysteresis will be discussed below). The compound has a spontaneous magnetic moment of \( M_{s} = 6.2 \mu_{B}/f.u. \) for field applied along [001], and no spontaneous component is present along the basal-plane directions. Therefore, \( Nd_{3}Ru_{4}Al_{12} \) displays a uniaxial magnetic anisotropy, with the magnetic moments pointing along the [001] axis, which is the easy-magnetization direction (EMD). A magnetic anisotropy is observed within the basal plane as well. The magnetization is lower when it is aligned along [120] than along the [100] axis. Here, [120] is the hardest-magnetization direction. An extension of the measurements up to 57 T reflects that the magnetization along the EMD further increases and reaches \( 8 \mu_{B}/f.u. \) at the highest field (inset in Fig. 3). Along the hard axes, the magnetization rises more steeply but still does not reach the value along the EMD.

FIG. 2. Temperature dependence of (a) the magnetization, M, and (b) the inverse magnetic susceptibility, \( 1/\chi \) , for a field of 1 T applied along the principal crystallographic directions; (c) the specific heat, C, and (d) the electrical resistivity, \( \rho \) , of \( Nd_{3}Ru_{4}Al_{12} \) . The insets in the panels (a), (c), and (d) show the low-temperature dependences of M at 0.1 T, C/T, and \( \rho \) , respectively.
It should be noted that, initially, the magnetization along the EMD is S shaped in fields up to 2 T, where it grows from 6.2 to \( 6.8 \mu_{B}/f.u \) . This is unlikely to be related to the magnetic hysteresis. Rather, we suggest it is due to changes in the magnetic structure.
The magnetization as a function of field applied along the easy axis at various temperatures is shown in Fig. 4. Initially,
TABLE II. Effective magnetic moment per Nd atom and Weiss temperatures for fields applied along the [100], [120], and [001] axes of \( Nd_{3}Ru_{4}Al_{12} \) obtained from fits using Eq. (1) in the indicated temperatures regions.
| [100] | [120] | [001] | |
| \( \mu_{\text{eff}}, \mu_{\text{B}}/\text{Nd atom} \) | 3.6 | 3.3 | 3.8 |
| \( \theta, \text{K} \) | -2 | +3 | +45 |
| \( \chi_{0}, \text{m}^{3} \text{mol}^{-1} \) | \( 3 \times 10^{-8} \) | \( 2 \times 10^{-8} \) | 0 |
| Temperature range, K | 45-300 | 65-300 | 80-230 |
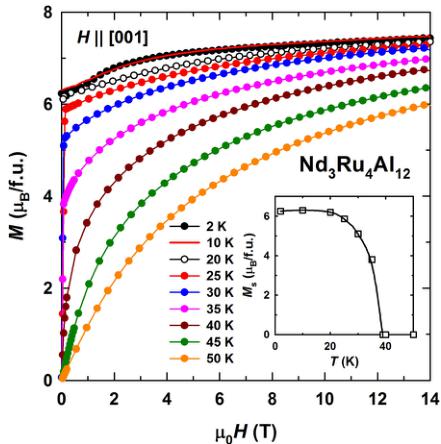
with rising temperature, \( M_{s} \) slightly increases and reaches \( 6.3 \mu_{B}/f.u. \) at 10 K. Simultaneously, the S shape becomes less pronounced and is no longer seen above 10 K. Upon approaching the Curie temperature, the spontaneous magnetic moment decreases steadily and falls to zero around 40 K as shown in the inset in Fig. 4 (the \( M_{s} \) values were determined from Arrott plots). \( M_{s} \) has a weak maximum at 10 K, similar to the temperature dependence of the magnetization measured in 1 and 0.1 T (see Fig. 2).
The magnetization as a function of field aligned along the hard axes is shown for various temperatures in Fig. 5. For field along [100], M reveals a weak convex curvature up to 14 T in the magnetically ordered state and becomes linear above the Curie temperature. The magnetization for fields along the [120] axis exhibits an even more pronounced curvature below \( T_{C} \) . This can be seen more clearly from the data obtained in pulsed magnetic fields (see inset in Fig. 3). Since \( Nd_{3}Ru_{4}Al_{12} \) displays a uniaxial anisotropy, its second-order anisotropy constant, \( K_{1} \) , is positive. The negative curvature of the hardest-axis magnetization curve suggests also a positive fourth-order anisotropy constant, \( K_{2} \) . In order to estimate \( K_{1} \) and \( K_{2} \) , we used the Sucksmith-Thompson method for a

FIG. 3. Magnetization as a function of fields applied along the principal crystallographic directions of \( Nd_{3}Ru_{4}Al_{12} \) at 2 K. The inset shows field-dependent magnetization data in pulsed magnetic fields up to 57 T.

FIG. 4. Magnetization as a function of field applied along the easy magnetization direction [001] of \( Nd_{3}Ru_{4}Al_{12} \) at various temperatures. The inset shows the temperature dependence of the spontaneous magnetic moment.
uniaxial ferromagnet [43]. The method is based on the relation
\[ \frac{H}{M}=\frac{2K_{1}}{M_{s}^{2}}+\frac{4K_{2}M^{2}}{M_{s}^{4}}, \quad (3) \]

FIG. 5. Magnetization for field applied along the hard-magnetization directions [100] and [120] of \( Nd_{3}Ru_{4}Al_{12} \) at variours temperatures. The inset shows the temperature dependence of the second- and fourth-order anisotropy constants, with the dashed lines as guides to the eye.

FIG. 6. Hysteresis loops for field applied along the [001] axis of \( Nd_{3}Ru_{4}Al_{12} \) between 2 and 20 K. The inset shows the temperature dependence of the coercivity where the solid line is a fit using \( \mu_{0}H_{\mathrm{c}}(T)=3.71\ \exp(-0.245\ T) \) .
that holds for fields applied along the hard magnetization direction. Since the [120] axis is hardest, we used these data to determine \( K_{1} \) and \( K_{2} \) . The temperature dependences of the anisotropy constants are given in the inset in Fig. 5. At low temperatures, the relation \( K_{1} < K_{2} \) holds ( \( K_{1} \approx 3 MJ m^{-3} \) and \( K_{2} \approx 3.5 MJ m^{-3} \) at 2 K). It changes to \( K_{1} > K_{2} \) around 30 K. The anisotropy constants determined from the [100]-magnetization data depend on temperature in a similar way with values approximately 20–30% lower (not shown for clarity of presentation). This makes it possible to estimate the magnetic anisotropy within the basal plane as the difference between the ratios \( (K_{1} + 2K_{2}) : (K_{1} + 2K_{2})_{[100]} - (K_{1} + 2K_{2})_{[120]} \approx -2.6 MJ m^{-3} \) . This reflects a strong magnetic anisotropy within the basal plane of \( Nd_{3}Ru_{4}Al_{12} \) . Anyway, the Sucksmith-Thompson method was developed for a one-sublattice ferromagnet. Since \( Nd_{3}Ru_{4}Al_{12} \) is a two-sublattice ferromagnet, as will be shown below from our neutron-diffraction data, the obtained \( K_{1} \) and \( K_{2} \) values should be regarded as rough estimates.
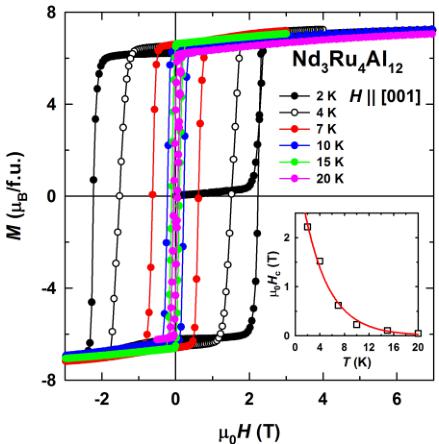
\( Nd_{3}Ru_{4}Al_{12} \) , being a strongly anisotropic ferromagnet, displays pronounced magnetic hysteresis. Hysteresis loops measured between 2 and 20 K along the EMD are presented in Fig. 6. The loops have an almost rectangular shape. The virgin curve at 2 K for the thermally demagnetized sample (cooled in zero field) has a very low initial susceptibility in a wide field interval. This suggests that the domain walls are frozen. They begin to move at the activation field where the steep rise in the magnetization is observed. Then the magnetization saturates in a narrow field interval. Above the saturation, the sample is in a single-domain state. At 2 K, the coercivity, \( H_{c} \) , reaches 2.2 T and decreases exponentially with increasing temperature (inset in Fig. 6) according to the empirical relation
\[ \mu_{0}H_{\mathrm{c}}(T)=3.71\exp(-0.245\ T). \quad (4) \]
For conventional ferromagnets for which the exchange energy is much larger than the anisotropy energy, the dominant contribution to the coercivity is provided by defects in the crystal structure. On the other hand, for strongly anisotropic ferromagnets with low exchange energy, the dominant mechanism of the magnetic hysteresis is the intrinsic coercivity of narrow domain walls \( [44–46] \) . For \( Nd_{3}Ru_{4}Al_{12} \) , the anisotropy energy \( (K_{1} + 2K_{2})/k_{B} \approx 240 K \) ( \( k_{B} \) is the Boltzmann constant) is much larger than the exchange energy given by \( T_{C} = 39 K \) . The domain-wall width can be estimated according to the expression \( [47] \) .
\[ \delta\approx\pi\sqrt{\frac{k_{\mathrm{B}}T_{\mathrm{C}}}{a(K_{1}+2K_{2})}}, \quad (5) \]
where \(a\) is the distance between magnetic atoms, \(a \approx 4 \mathring{\mathrm{A}}\). The estimate leads to 10 Å, i.e., the domain walls are of the order of a few interatomic distances. Thus, the large magnetic hysteresis with the strong temperature dependence is most likely due to the high intrinsic coercivity of narrow domain walls in \(\mathrm{Nd}_{3}\mathrm{Ru}_{4}\mathrm{Al}_{12}\).
Although \( Nd_{3}Ru_{4}Al_{12} \) is expected to be a simple ferromagnet in accordance with the earlier reports on polycrystalline samples [35,36], the nontrivial behavior of the magnetization as a function of temperature and magnetic field makes it necessary to use a microscopic technique in order to determine the magnetic structure of the compound. This motivated us to perform neutron-diffraction experiments on the single crystal.
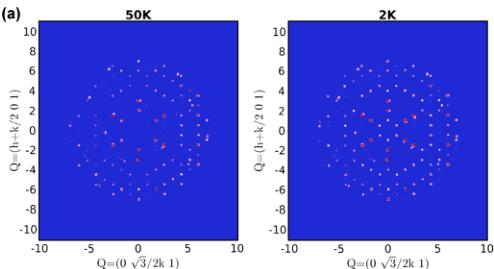
Figure 7(a) shows cuts in the hk1 planes of the reciprocal space of \( Nd_{3}Ru_{4}Al_{12} \) obtained from the PSD measurements at 50 and 2 K. In the paramagnetic state (at 50 K), the nuclear reflections observed are in agreement with the space group \( P6_{3}/mmc \) . Further refinements of the nuclear structure confirmed it to be consistent with the single-crystal x-ray diffraction study mentioned above, leading to final refinement factors \( R_{N}=3.50\% \) and \( wR_{N}=3.97\% \) (Table III). The apparently absent reflections in this map, as is the case of \( \{101\} \) in the center of the pattern [Fig. 7(a), left panel], are in reality very weak, which makes their separation from the background difficult. These reflections have very small nuclear structure factors, and calculations of intensity using the nuclear structure model from the refinement at 50 K have shown that the intensity of all the reflections of this family is very low.
As the temperature is lowered to 2 K [Fig. 7(a), right panel], all nuclear reflections with a nonzero component perpendicular to the scattering vector, Q, are strengthened, and no extra peaks appear in the \( (hk1) \) intensity map. This is consistent with a magnetic propagation vector k = 0, and the long-range ferromagnetic ordering of \( Nd_{3}Ru_{4}Al_{12} \) below \( T_{C} = 39 K \) , as established from our measurements presented above.
The intensity of magnetic diffraction in the case of an unpolarized neutron beam in a magnetically ordered crystal is given by (see, e.g., Ref. [48])
\[ I_{\mathrm{M}}(\mathbf{Q})\propto|\mathbf{F}_{\mathrm{M}}(\mathbf{Q})|^{2}-|\mathbf{e}\mathbf{F}_{\mathrm{M}}(\mathbf{Q})|^{2}, \quad (6) \]
where \( e = Q/|Q| \) is the unit vector along the scattering vector Q and \( \mathbf{F}_{\mathrm{M}}(\mathbf{Q}) \) is the magnetic structure factor. \( \mathbf{F}_{\mathrm{M}}(\mathbf{Q}) \) is an axial vector that depends on Q. Also, \( \mathbf{F}_{\mathrm{M}}(\mathbf{Q}) \) is the Fourier transform of the average local magnetic moment density \( \mathbf{M}_{\mathrm{M}}(\mathbf{r}) \) in the


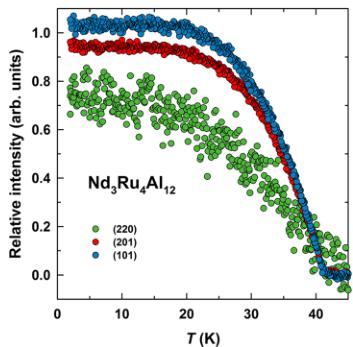
FIG. 7. Temperature dependence of the neutron-diffraction intensity in \( Nd_{3}Ru_{4}Al_{12} \) . (a) Diffraction maps of the \( (hk1) \) planes in the reciprocal space at 50 and 2 K, showing strengthening of the intensities with decreasing temperature. (b) Temperature dependence of the diffraction intensity of the reflections (220), (201), and (101) between 2 and 50 K.
lattice
\[ \mathbf{F}_{\mathrm{M}}(\mathbf{Q})=\int M_{\mathrm{M}}(\mathbf{r})\exp(2\pi i\mathbf{Q}\mathbf{r})d\mathbf{r}. \quad (7) \]
The magnetic-moment density describes the three-dimensional magnetic arrangement of the magnetic moments in a crystal and imposes symmetry constraints on \( \mathbf{F}_{\mathrm{M}}(\mathbf{Q}) \) . The symmetry operations allowed by the magnetic space (Shubnikov) group of the crystal impose certain symmetry-forced reflection absences, and additional extinctions result for specific orientations of the magnetic moments for certain magnetic structures.
A comprehensive list of absences and symmetry-forced form factors can be found in the Bilbao Crystallographic Server [49]. In particular, the program MAGNEXT [48] provides symmetry-adapted magnetic structure factors for each Shubnikov group.
To derive all possible magnetic structures compatible with the crystal structure and the propagation vector, we performed the refinement based on symmetry analysis and supported by the bulk-magnetization data. Strong prerequisites for an appropriate model to be chosen are a nonzero net magnetic moment originating from the Nd sublattice primarily and having a large [001]-projected axial component.
TABLE III. Results from the refinement of the single-crystal neutron data of \( Nd_{3}Ru_{4}Al_{12} \) collected at 50 and 2 K: component of the magnetic moment along [001] is \( m_{[001]} \) ; total magnetic moment \( M_{[001]} \) ; refinement factors R and wR. Errors refer to estimated standard deviations.
| Temperature | 50 K | 2 K | ||||
| Space group | \( P6_{3}/mm^{\prime}c^{\prime} \) | \( P6_{3}/mm^{\prime}c^{\prime} \( | \( Cm^{\prime}c^{\prime}m \) | |||
| Label | Nd1 | Nd1 | Nd1 | Nd2 | ||
| Position (x, 2x, 0.25) | 0.19106 | 0.19105 | 0.19105 | -0.38210 | ||
| Multiplicity | 6 | 6 | 2 | 4 | ||
| Symmetry contraints on m | - | 0, 0, \( m_{[001]} \) | 0, 0, \( m_{[001]} \) | |||
| \( m_{[001]}(\mu_{\mathrm{B}}) \) | - | 2.42(2) | 0.95(9) | 2.66(1) | ||
| \( M_{[001]}(\mu_{\mathrm{B}}/\mathrm{f.u.}) \) | - | 7.2 | 6.2 | |||
| Refinement factors: R, wR (%) | 2.17, 3.97 | 8.79, 14.64 | 6.66, 8.74 | |||
| Integrated intensity | ||||||
| Reflection | Nuclear observed | Total observed | Magnetic | Magnetic | ||
| Calculated | Observed \( ^{c} \) | Calculated | Observed \( ^{c} \) | |||
| 002 | 0 | 0 | 0 | 0 | 0 | 0 |
| 003 | 0 | 3.6 ± 2.3 | 0 | 0 | 0 | 0 |
| 103 | 16.6 | 38.9±0.5 | 1.5 | 18.8 (39%) | 0 | 4.3 (11%) |
| 101 \( ^{a} \) | 6.4 | 32.5±0.4 | 16.1 | 26.2 (77%) | 17.4 | 22.9 (70%) |
| 102 \( ^{a} \) | 1.1 | 16.6±0.4 | 1.8 | 14.8 (89%) | 2.6 | 14.1 (85%) |
| 220 | 131 | 177.9±1.8 | 4.3 | 6.4 (3%) | 20.5 | 15.2 (9%) |
| 211 \( ^{b} \) | 12.5 | 18.1±0.3 | 0.6 | 1.8 (10%) | 0.7 | 1 (6%) |
| 300 \( ^{b} \) | 29.8 | 40.7±0.6 | 6.8 | 6 (15%) | 0.1 | 1.6 (4%) |
\( ^{a} \) Stronger magnetic contributions to these reflections will appear if the moments are oriented along [001].
\( ^{b} \) Stronger magnetic contributions to these reflections will appear if the moments are in (110).
\( ^{c} \) Percentage of magnetic scattering relative to the total scattering is given in parentheses.
For the parent space group \( P6_{3}/mmc1' \) , there are 8 distinct “1-k” magnetic space groups of maximal symmetry consistent with the \( k=0 \) propagation vector. From this set, only the Shubnikov magnetic group \( P6_{3}/mm'c' \) (#194.8.1501 in the Opechowski-Guccione (OG) notation [50]) allows the ferromagnetic ordering of the Nd magnetic moments at the 6h site. For this space group, the glide plane \( c' \) gives the same extinction \( l=2n+1 \) for (hh) reflections for nuclear and magnetic contributions for atoms located at special positions (Nd and Ru1 at 2a). As can be seen by monitoring the evolution of the intensity of some reflections as a function of temperature, presented in Fig. 7(b), the reflection (220) appears to be of nuclear origin since its intensity is little affected by the onset of magnetic order at \( T_{C} \) . Nevertheless, this reflection has one of the strongest nuclear intensities, whereas the magnetic component of the scattering appearing on top is significantly weaker (Table III). On the other hand, the intensity of the reflections (101) and (201) clearly shows increased magnetic scattering intensity when compared to the respective nuclear contributions. This observation suggests that the Nd sublattice is the main responsible for the onset of the long-range magnetic ordering below 39 K. In fact, due to the position of the Ru1 atoms in the crystallographic unit cell (site 2a), a possible Ru ferromagnetic order (along [001]) does not contribute to the magnetic intensity of (hk1) reflections with \( l=2n+1 \) . For Ru2 in the position 6g, the same arguments would apply only when considering that its magnetic-moment component perpendicular to [001] is zero.
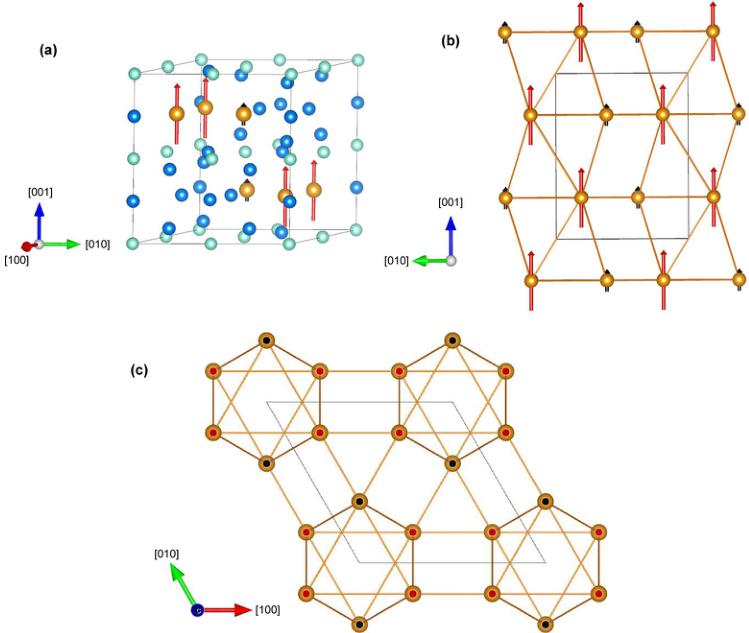
The magnetic structure solved in the Shubnikov group \( P6_{3}/mm^{\prime}c^{\prime} \) implies that the components of the Nd magnetic moment are of the form \( (0\ 0\ m_{[001]}) \) , where \( m_{[001]} \) is the component parallel to [001]. The refinement using Jana2006 shows that, for each Nd atom, this component is \( m_{[001]} = 2.42(2)\ \mu_{B} \) , yielding a total magnetic moment of \( m_{[001]} \approx 7.2\ \mu_{B}/f.u. \) at 2 K (Table III). This value is larger than the magnetic moment determined by the magnetic bulk measurements at 2 K ( \( \approx 6.2\ \mu_{B}/f.u. \) ). It was also found that some magnetic reflections of the type \( (h - 2h\ l) \) , \( (h\ h\ l) \) , and \( (-2k\ k\ l) \) are observed despite having zero calculated structure factor. Additionally, the best refinement factors for this magnetic model were found to be somewhat enhanced ( \( R_{M} = 8.79\% \) and \( wR_{M} = 14.64\% \) ). Altogether, this prompted us to search for another possible solution in the same group of isotropy but lowering the symmetry to orthorhombic.
The magnetic space group \( Cm^{\prime}c^{\prime}m \) (#63.6.516 in OG notation) is a subgroup of \( P6_{3}/mm^{\prime}c^{\prime} \) allowing the ferromagnetic alignment of the Nd magnetic moments parallel to [001] (by formation of three magnetic domains). For this magnetic space group, the 6h Wyckoff site is split into two different positions: 4c (Nd1) and 8g (Nd2). For both positions, the components of the magnetic moment are of the form \( (0\ 0\ m_{[001]})_{0} \) . The refinement of the magnetic structure was carried out, allowing two free parameters, i.e., \( m_{[001]} \) of both Nd sites. We obtained the moments \( m_{[001]} \) (Nd1) = 0.95(9) \( \mu_{B} \) and \( m_{[001]} \) (Nd2) = 2.66(1) \( \mu_{B} \) , as listed in Table III. These values lead to a total magnetic moment of \( m_{[001]} \approx 6.3\ \mu_{B}/f.u. \) at 2 K, in excellent agreement with the moment determined from the bulk magnetization. Moreover, the absence of magnetic reflections of type (00l), with \( l = 2n + 1 \) , indicates that the principal component of the Nd magnetic moments is oriented along [001] (Table III). Additionally, for this magnetic structure, all observed magnetic reflections have nonzero structure factors, including the

FIG. 8. Ferromagnetic structure of \( Nd_{3}Ru_{4}Al_{12} \) at 2 K. The two Nd positions in the centrosymmetric Shubnikov group \( Cm^{\prime}c^{\prime}m \) have magnetic moments of different magnitude and are represented by black (Nd1: 4c site) and red (Nd2: 8g site) arrows. (a) The unit cell is represented in the hexagonal setting (the colors of the elements in the unit cell are the same as in Fig. 1). (b) and (c) The projections of the Nd magnetic lattice show the arrangement of the two different magnetic sites with respect to the principal crystallographic directions.
reflections \( (h - 2h l) \) , \( (h h l) \) , and \( (-2k k l) \) , which is also seen in considerably smaller refinement factors \( (R_{\mathrm{M}} = 6.66\% \) and \( w R_{\mathrm{M}} = 8.74\%) \) when compared with the higher-symmetry order.
The low-symmetry ferromagnetic configuration is rather unusual and prompted us to fit the data as well by an equal-moment model. This, however, leads to worse refinement factors (similar to those of the first solution) and poorer agreement with the experimental data. It appears that unequal Nd moments are necessary to explain the observed intensities of the reflections \( (h - 2h\ l) \) , \( (h\ h\ l) \) , and \( (-2k\ k\ l) \) . The magnetic ordering of the Nd atoms breaks the sixfold rotational symmetry of the nuclear structure. The magnetic structure of \( Nd_{3}Ru_{4}Al_{12} \) refined at 2 K is shown in Fig. 8.
The magnetic structure of \( Nd_{3}Ru_{4}Al_{12} \) bears certain similarities to that of the isostructural material \( Dy_{3}Ru_{4}Al_{12} \) that, albeit antiferromagnetic, has the largest component of the Dy magnetic moment oriented along the [001] axis as well [42]. The magnetic moments of another antiferromagnetically ordered member of the series, \( Tb_{3}Ru_{4}Al_{12} \) , were also suggested to be aligned predominantly along the same direction [51]. This situation is not surprising taking into account that \( Nd^{3+} \) , \( Tb^{3+} \) , and \( Dy^{3+} \) ions have the same (negative) sign of the second-order Stevens factor that plays a crucial role for the determination of the magnetic-anisotropy type [5].
IV. DISCUSSION
This paper indicates that \( Nd_{3}Ru_{4}Al_{12} \) is a ferromagnet ( \( T_{C} = 39 K \) ) with strong uniaxial magnetic anisotropy. Since the magnetic moments are aligned along the [001] axis in \( Nd_{3}Ru_{4}Al_{12} \) as opposed to \( U_{3}Ru_{4}Al_{12} \) , where they are confined to the basal plane [34], we have demonstrated that the single-ion and two-ion mechanisms may lead to distinct anisotropies.
Apart from the magnetic anisotropy, \( Nd_{3}Ru_{4}Al_{12} \) has been found to be interesting from another perspective. Evidently, the most peculiar finding is the reduced Nd magnetic moments with \( Nd_{3}Ru_{4}Al_{12} \) being a two-sublattice ferromagnet. \( Nd^{3+} \) is a Kramers ion, and the crystal-field levels are, therefore, at least doubly degenerated. It is known that the crystalline electric field (CEF) might quench the orbital magnetic moment of a given atom [52]. Due to the strong spin-orbit coupling of rare-earth ions, the CEF may reduce both the spin and orbital moments. Since Nd is a light lanthanide and, therefore, its total angular momentum is J = L - S (L is the orbital and S the spin angular momentum), the effect of CEF might be quite pronounced for \( Nd_{3}Ru_{4}Al_{12} \) . The energy between the ground state and the first excited crystal field state varies typically between 10 and 100 K and might, therefore, exceed the exchange energy, of order 40 K, of the compound.
Reduced Nd magnetic moments are quite common in Nd-based intermetallic compounds, e.g., in \( Nd_{6}Fe_{13-x}Ga_{1+x} \) (x = 0, 1) [53], \( Nd_{2}Co_{17-x}Ga_{x} \) (x = 5, 6, and 7) [54], \( NdNiGe_{2} \) [55], and \( NdSi_{x} \) (1.67 ≤ x ≤ 2) [56]. The effects of CEF are also pronounced for pure neodymium that orders antiferromagnetically at \( T_{N} = 19.9 \) K with a complex magnetic structure [57–63]. In the double hexagonal close-packed crystal structure of neodymium, there are three inequivalent atomic sites. Two sites having hexagonal symmetry carry a magnetic moment of 2.3 \( \mu_{B} \) , whereas the third position whose symmetry is cubic has a lower magnetic moment of 1.8 \( \mu_{B} \) [57,58,60]. These data are qualitatively similar to what we observed for \( Nd_{3}Ru_{4}Al_{12} \) with Nd moments of 2.66 and 0.95 \( \mu_{B} \) .
However, since in \( Nd_{3}Ru_{4}Al_{12} \) all Nd atoms reside in the same crystallographic position, the different Nd magnetic moments might not only be caused by the CEF. Competing exchange and anisotropic interactions frequently lead to reduced magnetic moments as found, e.g., for \( R_{5}X_{3} \) (X = Si, Sb, Ge) [64–69] and \( R_{2}Ni_{2}T \) (T = In, Pb) [70–72]. In \( Nd_{3}Ru_{4}Al_{12} \) , the Nd atoms form a triangular lattice parallel to the basal plane (Fig. 1). This lattice can be visualized as a distorted kagome net; therefore, the Nd atoms might be subject to geometrical frustration. The complex noncollinear antiferromagnetic structures of the isostructural compounds with R = Dy and U serve as fingerprints of geometrical frustration [34,38]. Although \( Nd_{3}Ru_{4}Al_{12} \) exhibits a collinear ferromagnetic structure, competing interactions due to geometrical frustration might affect the absolute value of the Nd magnetic moment rather than its orientation.
Application of magnetic fields enhances the magnetic moment of \( Nd_{3}Ru_{4}Al_{12} \) beyond \( M_{s} \) (Figs. 3 and 4). In applied magnetic field, the total ordered moment of pure neodymium can be substantially increased, as observed by neutron scattering [58]. Taking into account this finding of Ref. [58], we suggest that the initial magnetization rise along the EMD of \( Nd_{3}Ru_{4}Al_{12} \) in fields up to 2 T (see Figs. 3 and 4) might be related to an increase of the Nd magnetic moment. At present, it is hard to conclude whether one or both Nd sites have this behavior. A neutron-diffraction experiment in applied magnetic field is highly desirable.
V. CONCLUSIONS
In this paper, we studied the magnetic properties of a \( Nd_{3}Ru_{4}Al_{12} \) single crystal. The material orders ferromagnetically at the Curie temperature of 39 K. A strong uniaxial magnetic anisotropy is found that leads to a large magnetic hysteresis of narrow domain walls. The second- and fourth-order anisotropy constants are estimated to be about 3 and \( 3.5~MJ~m^{-3} \) , respectively. The spontaneous magnetic moment along the easy [001] axis is \( 6.2~\mu_{B}/f.u. \) at 2 K. The collinear magnetic structure of \( Nd_{3}Ru_{4}Al_{12} \) is described within the orthorhombic \( Cm^{\prime}c^{\prime}m \) space group. The symmetry of the magnetic space group implies a splitting of the crystallographic position of Nd, 6h, into two inequivalent magnetic sites, 4c (Nd1) and 8g (Nd2). Both, the Nd1 and Nd2 atoms exhibit reduced magnetic moments of 0.95 and \( 2.66~\mu_{B} \) , respectively, in comparison with the free \( Nd^{3+} \) -ion value ( \( 3.28~\mu_{B} \) ), which is likely due to crystal-field effects and competing exchange and anisotropy interactions. This paper allows a comparison between the magnetic anisotropies of direct elemental analogs in the lanthanide and actinide series. The single-ion anisotropy of \( Nd_{3}Ru_{4}Al_{12} \) leads to uniaxial and the two-ion anisotropy of \( U_{3}Ru_{4}Al_{12} \) to planar anisotropies.
ACKNOWLEDGMENTS
The crystallographic part was supported by Project No. 15-12653S of the Czech Science Foundation using instruments of the ASTRA Lab established within the Operation Program Prague – Competitiveness, Project No. CZ.2.16/3.1.00/24510. Measurements of some electronic properties were supported by Project No. 16-03593S of the Czech Science Foundation. This work was partly performed in Magnetism and Low Temperatures Laboratories (MLTL) (http://mltl.eu/), which are supported within the program of Czech Research Infrastructures (Project No. LM2011025). We acknowledge the support of High Magnetic Field Laboratory (HLD) at Helmholtz-Zentrum Dresden-Rossendorf (HZDR), a member of the European Magnetic Field Laboratory (EMFL).
[1] J. H. Van Vleck, Phys. Rev. 52, 1178 (1937).
[2] J. J. M. Franse and R. J. Radwański, in Handbook of Magnetic Materials, edited by K. H. J. Buschow (Elsevier, Amsterdam, 1993), Vol. 7, p. 307.
[3] A. Furrer, F. Juranyi, K. W. Krämer, M. Schneider, and Th. Strässle, Phys. Rev. B 83, 024404 (2011).
[4] M. Doerr, A. Haase, M. Loewenhaupt, M. Rotter, M. Bartkowiak, R. Daou, E. Kampert, J. A. A. J. Perenboom, and T. Tsutaoka, Phys. Rev. B 82, 024422 (2010).
[5] M. D. Kuz'min and A. M. Tishin, in Handbook of Magnetic Materials, edited by K. H. J. Buschow (Elsevier Amsterdam, 2008), Vol. 17, p. 149.
[6] V. Sechovský and L. Havela, in Handbook of Magnetic Materials, edited by K. H. J. Buschow (Elsevier. Amsterdam, 1998), Vol. 11, p. 1.
[7] K. H. J. Buschow, A. M. van Diepen, and H. W. de Wijn, Solid State Commun. 15, 903 (1974).
[8] K. H. J. Buschow, J. Magn. Magn. Mater. 100, 79 (1991).
[9] H.-S. Li and J. M. D. Coey, in Handbook of Magnetic Materials, edited by K. H. J. Buschow (Elsevier), Amsterdam, 1991), Vol. 6, p. 1.
[10] R. Grössinger, X. K. Sun, R. Eibler, K. H. J. Buschow, and H. R. Kirchmayr, Magn. Magn. Mater. 58, 55 (1986).
[11] K. Strnat, G. Hoffer, J. Olson, W. Ostertag, and J. J. Becker, J. Appl. Phys. 38, 1001 (1967).
[12] J. Croat, J. F. Herbst, R. W. Lee, and F. E. Pinkerton, J. Appl. Phys. 55, 2078 (1984).
[13] M. Sagawa, S. Fujimura, M. Togawa, and Y. Matsuura, J. Appl. Phys. 55, 2083 (1984).
[14] K. H. J. Buschow, in Handbook of Magnetic Materials, edited by E. P. Wohlfarth and K. H. J. Buschow (Elsevier, Amsterdam, 1988), Vol. 4, p. 1.
[15] K. J. Strnat, in Handbook of Magnetic Materials, edited by E. P. Wohlfarth and K.H. J. Buschow (Elsevier, Amsterdam, 1988), Vol. 4, 131.
[16] G. H. Lander, M. S. S. Brooks, and B. Johansson, Phys. Rev. B 43, 13672 (1991).
[17] F. U. Hillebrecht, D. D. Sarma, and N. Martensson, Phys. Rev. B 33, 4376(R) (1986).
[18] T. Endstra, G. J. Nieuwenhuys, and J. A. Mydosh, Phys. Rev. B 48, 9595 (1993).
[19] J. Gal, F. J. Litterst, W. Potzel, J. Moser, U. Potzel, G. M. Kalvius, S. Fredo, and S. Tapuchi, Phys. Rev. B 36, 2457(R) (1987).
[20] A. V. Andreev, R. Z. Levitin, Y. F. Popov, and R. Y. Yumaguzhin, Sov. Phys. Solid State 27, 1145 (1985).
[21] K. Prokeš and A. Gukasov, Phys. Rev. B 79, 024406 (2009).
[22] P. H. Frings, J. J. M. Franse, A. Menovsky, S. Zemrili, and B. Barbara, J. Magn. Magn. Mater. 54–57, 541 (1986).
[23] E. Brück, H. Nakotte, F. R. de Boer, P. F. de Châtel, H. P. van der Meulen, J. J. M. Franse, A. A. Menovsky, N. H. Kim-Ngan, L. Havel, V. Sechovsky, J. A. A. J. Perenboom, N. C. Tuan, and J. Sebek, Phys. Rev. B 49, 8852 (1994).
[24] M. Samsel-Czekala, E. Talik, R. Troć, and J. Stepień-Damm, Phys. Rev. B 77, 155113 (2008).
[25] M. Samsel-Czekala, E. Talik, and R. Troć, Phys. Rev. B 78, 245120 (2008).
[26] K. Prokeš, H. Nakotte, M. I. Bartashevich, M. Doerr, and V. Sechovský, Phys. Rev. B 68, 014405 (2003).
[27] P. F. de Châtel, K. Prokeš, H. Nakotte, A. Purwanto, V. Sechovský, L. Havela, E. Brück, R. A. Robinson, and F. R. de Boer, J. Magn. Magn. Mater. 177–181, 785 (1998).
[28] Y. Andoh, H. Fujii, H. Fujiwara, and T. Okamoto, J. Phys. Soc. Jpn. 51, 435 (1982).
[29] Z. Kakol and H. Figiel, Physica B+C 130, 312 (1985).
[30] R. E. Gladyshevskii, O. R. Strusiewicz, K. Cenzual, and E. Parthe, Acta Cryst. B 49, 474 (1993).
[31] J. Niermann and W. Jeitschko, Z. Anorg. Allg. Chem. 628, 2549 (2002).
[32] N. G. Bukhan'ko, A. I. Tursina, S. V. Malyshev, A. V. Gribanov, Yu. D. Seropegin, and O. I. Bodak, J. Alloys Compd. 367, 149 (2004).
[33] M. Pasturel, O. Tougait, M. Potel, T. Roisnel, K. Wochowski, H. Noël, and R. Troé, J. Phys.: Condens. Matter 21, 125401 (2009).
[34] R. Troć, M. Pasturel, O. Tougait, A. P. Sazonov, A. Gukasov, C. Sulkowski, and H. Noël, Phys. Rev. B 85, 064412 (2012).
[35] W. Ge, H. Ohta, Ch. Michioka, and K. Yoshimura, J. Phys.: Conf. Series 344, 012023 (2012).
[36] W. Ge, C. Michioka, H. Ohta, and K. Yoshimura, Solid State Comm. 195, 1 (2014).
[37] CrysAris PRO, Agilent Technologies, Version 1.171.37.31.
[38] L. Palatinus and G. Chapuis, J. Appl. Cryst. 40, 786 (2007).
[39] V. Petříček, M. Dušek, and L. Palatinus, Z. Kristallogr. 229, 345 (2014).
[40] Y. Skourski, M. D. Kuz'min, K. P. Skokov, A. V. Andreev, and J. Wosnitza, Phys. Rev. B 83, 214420 (2011).
[41] A. Gukasov, A. Goujon, J.-L. Meuriot, Ch. Person, G. Exil, and G. Koskas, Physica B 397, 131 (2007).
[42] D. I. Gorbunov, M. S. Henriques, A. V. Andreev, A. Gukasov, V. Petříček, N. V. Baranov, Y. Skourski, V. Eigner, M. Paukov, J. Prokleška, and A. P. Gonçalves, Phys. Rev. B 90, 094405 (2014).
[43] W. Sucksmith and J. E. Thompson, Proc. Roy. Soc. London A 225, 362 (1954).
[44] H. R. Hilzinger and H. Kronmüller, Phys. Status Solidi B 54, 593 (1972).
[45] B. Barbara, G. Fillion, D. Gignoux, and R. Lemaire, Solid State Commun. 10, 1149 (1972).
[46] A. S. Yermolenko and A. F. Rozhda, Phys. Met. Metallogr. 44, 70 (1977).
[47] J. M. D. Coey, Magnetism and Magnetic Materials (Cambridge University Press, Cambridge, 2014).
[48] S. V. Gallego, E. S. Tasci, G. de la Flor, J. M. Perez-Mato, and M. I. Aroyo, J. Appl. Cryst. 45, 1236 (2012).
[49] M. I. Aroyo, J. M. Perez-Mato, D. Orobengoa, E. Tasci, G. de la Flor, and A. Kirov, Bulg. Chem. Commun. 43, 183 (2011).
[50] W. Opechowski and R. Guccione, in Magnetic Symmetry In Magnetism, edited by G. T. Rado and H. Suhl (Academic Press, New York, 1965), Vol. II, Part A, pp. 105–165.
[51] D. I. Gorbunov, S. Henriques, A. V. Andreev, Y. Skourski, and M. Dušek, J. Alloys Compd. 634, 115 (2015).
[52] S. Legvold, in Handbook of Magnetic Materials, edited by E. P. Wohlfarth (Elsevier, Amsterdam, 1980), Vol. 1, p. 183.
[53] P. Schobinger-Papamantellos, K. H. J. Buschow, and C. Ritter, J. Alloys Compd. 359, 10 (2003).
[54] O. Moze, L. Giovanelli, W. Kockelmann, C. H. de Groot, F. R. de Boer, and K. H. J. Buschow, J. Magn. Magn. Mater. 189, 329 (1998).
[55] P. Schobinger-Paramantellos, A. Krimmel, A. Grauel, and K. H. J. Buschow, J. Magn. Magn. Mater.125, 151 (1993).
[56] P. Schobinger-Papamantellos, K. H. J. Buschow, and P. Fischer, J. Magn. Magn. Mater. 97, 53 (1991).
[57] R. M. Moon, J. W. Cable, and W. C. Koehler, J. Appl. Phys. 35, 1041 (1964).
[58] T. Johansson, B. Lebech, M. Nielsen, H. Bjerrum Møller, and A. R. Mackintosh, Phys. Rev. Lett. 25, 524 (1970).
[59] B. Lebech, J. Als-Nielsen, and K. A. McEwen, Phys. Rev. Lett. 43, 65 (1979).
[60] B. Lebech, J. Appl. Phys. 52, 2019 (1981).
[61] R. M. Moon, B. Lebech, and J. R. Thompson, Phys. Rev. B 27, 354 (1983).
[62] B. Lebech, J. Wolny, and R. M. Moon, J. Phys.: Condens. Matter 6, 5201 (1994).
[63] D. Watson, E. M. Forgan, W. J. Nuttall, W. G. Stirling, and D. Fort, Phys. Rev. B 53, 726 (1996).
[64] J. P. Semitelou and J. K. Yakinthos, J. Magn. Magn. Mater. 265, 152 (2003).
[65] A. V. Morozkin, O. Isnard, R. Nirmala, and S. K. Malik, J. Alloys Compd. 470, 20 (2009).
[66] J. K. Yakinthos, I. P. Semitelou, and E. Roudaut, Solid State Commun. 59, 227 (1986).
[67] I. P. Semitelou, J. K. Yakinthos, and E. Roudaut, J. Phys. Chem. Solids 56, 891 (1995).
[68] P. Schobinger-Papamantellos and K. H. J. Buschow, J. Magn. Magn. Mater. 49, 349 (1985).
[69] R. Nirmala, A. V. Morozkin, A. K. Nigam, J. Lamsal, W. B. Yelon, O. Isnard, S. A. Granovsky, K. Kamala Bharathi, S. Quezado, and S. K. Malik, J. Appl. Phys. 109, 07A716 (2011).
[70] K. Prokeš, E. Mužoz-Sandoval, A. D. Chinchure, and J. A. Mydosh, Phys. Rev. B 68, 134427 (2003).
[71] K. Prokeš, E. Mužoz-Sandoval, A. D, Chinchure, and J. A. Mydosh, Phys. Rev. B 78, 014425 (2008).
[72] A. Szytuła, S. Baran, A. Hoser, Y. M. Kalychak, B. Penc, and Y. Tyvanchuk, Acta Phys. Polon. A 124, 994 (2013).