| Transition Temperature | 39 K |
|---|---|
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pa-3 (#205) |
| Magnetic Space Group | Pa-3 (#205.33) |
| Magnetic Point Group | m-3 (29.1.109) |
| Lattice Parameters | 5.68700 5.68700 5.68700 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrevb.93.024409 |
| Reference | S. Yano, D. Louca, J. Yang, U. Chatterjee, D.E. Bugaris, D.Y. Chung, L. Peng, M. Grayson and M.G. Kanatzidis, Physical Review B (2016) 93. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Ni1 | Ni | 0.569 | 0.569 | 0.569 | 0.99 |
Magnetic structure of NiS_{2-x}Se_{x}
S. Yano, \( ^{1,*} \) Despina Louca, \( ^{1,\dagger} \) J. Yang, \( ^{1} \) U. Chatterjee, \( ^{1} \) D. E. Bugaris, \( ^{2} \) D. Y. Chung, \( ^{2} \) L. Peng, \( ^{3} \) M. Grayson, \( ^{3} \) and Mercouri G. Kanatzidis \( ^{4} \)
\( ^{1} \) Department of Physics, University of Virginia, Charlottesville, Virginia 22904, USA
\( ^{2} \) Materials Science Division, Argonne National Laboratory, Argonne, Illinois 60439, USA
\( ^{3} \) Department of Electrical Engineering and Computer Science, and Department of Applied Physics, Northwestern University, Evanston, Illinois 60208, USA
\( ^{4} \) Department of Chemistry, Northwestern University, Evanston, Illinois 60208, USA
(Received 20 April 2015; revised manuscript received 23 November 2015; published 15 January 2016)
\( NiS_{2-2x}Se_{x} \) is revisited to determine the magnetic structure using neutron diffraction and magnetic representational analysis. Upon cooling, the insulating parent compound, \( NiS_{2} \) , becomes antiferromagnetic with two successive magnetic transitions. The first transition (M1) occurs at \( T_{N} \sim 39 \) K with \( \Gamma_{1}\psi_{1} \) symmetry and a magnetic propagation vector of \( k = (000) \) . The second transition (M2) occurs at \( T_{N} \sim 30 \) K with \( k = (0.5, 0.5, 0.5) \) and a \( \Gamma_{1}\psi_{2} \) symmetry with face-centered translations, giving rise to four possible magnetic domains. With doping, the system becomes metallic. The transition to the M2 state is suppressed prior to x = 0.4 while the M1 state persists. The M1 magnetic structure gradually vanishes by x \( \sim 0.8 \) at a lower concentration than previously reported. The details of the magnetic structures are provided.
DOI: 10.1103/PhysRevB.93.024409
I. INTRODUCTION
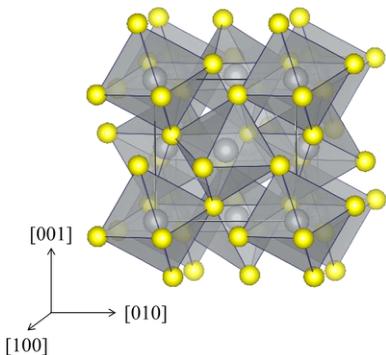
The cubic pyrite crystal \( NiS_{2-x}Se_{x} \) is a Mott insulator prototype. Mott insulators and the metal-insulator transition (MIT) they can exhibit due to strong electron correlations have been at the forefront of condensed-matter research. A Mott insulator is associated with antiferromagnetism (AFM) as well as an energy gap [1]. Typically, the energy scale associated with the gap is much larger than the magnetic exchange interaction. The parent compound \( NiS_{2} \) adopts a primitive cubic structure with the \( Pa\overline{3} \) symmetry shown in Fig. 1(a) and with a magnetic structure that is quite complex. The crystal structure consists of a network of \( NiS_{6} \) octahedra that create face-centered-cubic (fcc) Ni sublattice sites. The S ions can form dimers in which an apical S from one octahedron bonds to an equatorial S from another octahedron forming a dumbbell with a bond length of \( \sim2.1\ \AA \) [2,3]. As the Mott insulator is perturbed by the chemical substitution of Se for S (chemical pressure), the system is driven to the MIT. Contrary to expectations, however, magnetic exchange survives deep into the metallic regime. To shed light on this effect, we investigate how the AFM behavior is altered as a function of chemical pressure using neutron scattering.
The parent compound exhibits two successive magnetic transitions. Upon cooling, the first magnetic transition is observed to a state with a characteristic wave vector, \( k = (000) \) . This is referred to as the M1 magnetic structure, and it has a Néel transition temperature of \( T_{N_{1}} = 39.2 \) K [4,5]. The M1 state has a noncollinear spin ordering of the fcc sublattice of Ni ions [4,6] with a magnetic moment of \( 1.0\mu_{B} \) . The second magnetic transition is observed upon further cooling to a state with a characteristic wave vector, \( k = (\frac{1}{2}\frac{1}{2}\frac{1}{2}) \) , and a \( T_{N_{2}} = 29.75 \) K. Little is known of the spin structure of this so called M2 magnetic phase.
Polarized and unpolarized neutron scattering measurements on single crystals \( [4,7] \) were inconclusive of the spin configuration. Of the 12 kinds of domains the M2 magnetic structure can have, it has not been possible to distinguish its spin arrangement even by polarized neutron scattering. More recently, a single-crystal x-ray diffraction measurement showed that a \( (\frac{1}{2}\frac{1}{2}\frac{1}{2}) \( superlattice peak is present at the M2 transition \) [8] \( . The presence of the superlattice peak has been attributed to charge ordering, with the possibility of coexistence with the M2 magnetic structure. Since both the M1 and M2 structures are antiferromagnetic, a condition is utilized here that allows them to coexist on the fcc Ni sublattice and enables us to solve the magnetic structure of both phases. Thus, we focus on the magnetic structure determination of the M1 and M2 phases using neutron scattering and magnetic point group theory. ## II. EXPERIMENT Four samples with x = 0, 0.4, 0.6, and 0.8 of about 2 g each were measured using neutron powder diffraction. Handling of all starting materials was performed in the glove box under an inert Ar atmosphere. Ni powder (Alfa Aesar, 99.8%) was used as received. Pieces of S (Mation, 99.999%) and Se (Alfa Aesar, 99.999%) were ground to a fine powder with a mortar and pestle prior to use. Polycrystalline samples of \( NiS_{2-x}Se_{x} \) were prepared from stoichiometric mixtures of the elements (a slight excess of S was utilized to prepare phase-pure \( NiS_{2} \) ). The reaction mixtures were thoroughly ground together with a mortar and pestle and then loaded into thick-walled quartz tubes that were sealed under vacuum. Due to the volatility of S, the x = 0 sample was prereacted at lower temperatures of 400, 600, and 700 °C, respectively, with intermediate grinding. It was then annealed at a final temperature of 730 °C for 13 h. The x = 0.4, 0.6, and 0.8 samples underwent two cycles of heating directly at 730 °C.

FIG. 1. The crystal structure of \( NiS_{2-x}Se_{x} \) . Ni sites at the center of the octahedra are coordinated by S. The octahedra form a face-centered lattice.
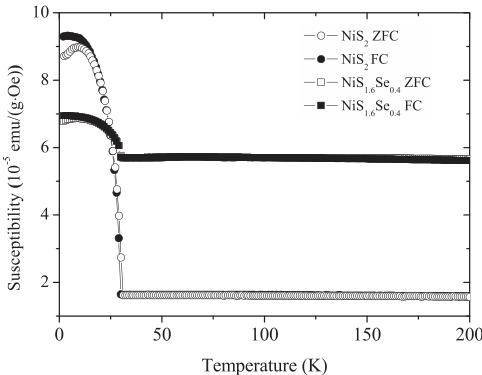
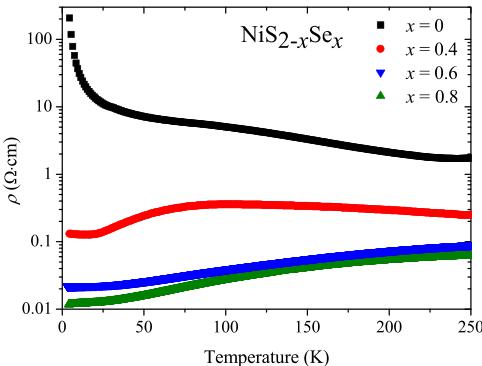
for 12 and 48 h, respectively, with intermediate grinding. Initial characterization of the gray powders was conducted by laboratory powder x-ray diffraction. The bulk magnetic susceptibility for the x = 0 and 0.4 compositions is shown in Fig. 2. Both samples show a magnetic transition. The transition temperature in x = 0 is about 30 K, while in x = 0.4 it is about 33 K. These results are consistent with previous reports. The transport data for x = 0, 0.4, 0.6, and 0.8 are shown in Fig. 3. The parent compound is insulating while the x = 0.4 composition shows an MIT. The x = 0.6 and 0.8 compositions are metallic from room temperature and below. These data are consistent with published results. The neutron experiment was carried out at the Nanoscale Ordered Materials Diffractometer (NOMAD) at the Spallation Neutron Source (SNS) of Oak Ridge National Laboratory, which is a high-flux, medium-resolution diffractometer [9]. The powder samples were placed in vanadium cans using He as the exchange

FIG. 2. The zero-field-cooled (ZFC) and field-cooled (FC) magnetic susceptibility as a function of temperature for the parent compound and the x = 0.4.

FIG. 3. The resistivity plotted in log scale for the x = 0.0, 0.4, 0.6, and 0.8 compositions as a function of temperature. The x = 0 is insulating, while the other compositions show an insulator-to-metal transition.
gas and loaded on a cryostat. Data were collected for 1 h at each temperature. The background was properly subtracted by measuring the empty vanadium can and the empty cryostat and properly normalized using a vanadium rod as a standard. The representational analysis was carried out using the program SARAH-REPRESENTATIONAL ANALYSIS [10].
III. MAGNETIC ANALYSIS OF \( NiS_{2} \)
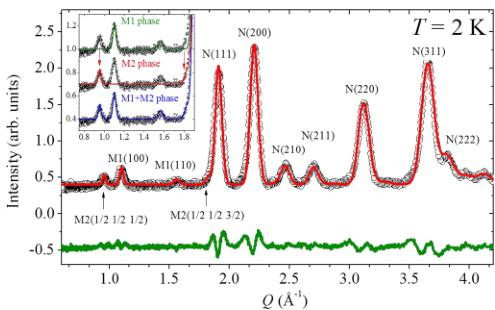
The \( NiS_{2} \) diffraction pattern of Fig. 4 corresponds to data collected at 2 K. The analysis of the nuclear pattern yields a cubic symmetry of Pa3 as reported in the literature with a lattice constant \( a = 5.689 \, \AA \) . The Ni ion resides at the face-centered lattice sites. The magnetic peaks in the spectrum are indexed as either belonging to the M1 or M2 magnetic phases. Magnetic point group theory was used to fit the data. Within the constraints of nuclear symmetry, the

FIG. 4. The neutron diffraction pattern of the parent compound, \( NiS_{2} \) , collected at 2 K. The open black circle and solid red line correspond to the observed and calculated intensities. The inset shows the fitted magnetic peaks with either M1 or M2 structure, and combined \( M1 + M2 \) structures.

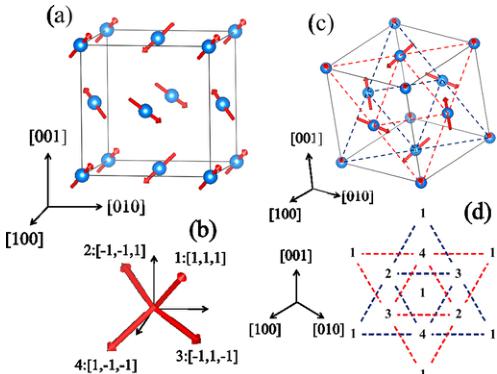
FIG. 5. (a) The M1 magnetic structure in \( NiS_{2} \) using the \( \Gamma_{1}\psi_{1} \) representation. The Ni spins order antiferromagnetically and align in the [111] direction. (b) The direction of the four moments. (c) The M2 magnetic structure using the \( \Gamma_{1}\psi_{2} \) representation involves doubling of the unit cell in all directions. (d) The triangle lattice as viewed from the c axis with the four moment directions indicated on the interpenetrating triangles.
magnetic irreducible representations that can reproduce the antiferromagnetic structures of the \(M1\) and \(M2\) phases are \(\Gamma_{1}\psi_{1}\) with \(k=(100)\), and \(\Gamma_{1}\psi_{2}\) with \(k=(\frac{1}{2}\frac{1}{2})\), respectively, and they will be described in detail below. The goodness of fit from the refinement yields \(R_{p}=26.8\%\), \(R_{\mathrm{wp}}=14.6\%\), \(R_{\mathrm{exp}}=6.08\%\), and \(\chi^{2}=5.76\). Upon cooling below \(T_{N1}\), two magnetic peaks first appear, indexed as \((110)_{M}\) and \((100)_{M}\). They are assigned to the magnetic structure of \(\Gamma_{1}\psi_{1}\) with the propagation vector \(k=(000)\). The proposed magnetic pattern is shown in Fig. 5(a), which shows the spins tilt along the (111) direction. The results from the magnetic moment refinement are summarized in Table I. This is consistent with previous results from a Mössbauer study [6].
Upon further cooling, the second magnetic transition to the M2 phase with the \( k = \left(\frac{1}{2} \frac{1}{2} \frac{1}{2}\right) \) propagation vector sets in, yielding two magnetic peaks at \( \left(\frac{1}{2} \frac{1}{2} \frac{2}{2}\right) \) and \( \left(\frac{1}{2} \frac{1}{2} \right) \) . These are identified in Fig. 2 and also shown in the inset. The M2 magnetic cell is far more complex than the M1 cell. To determine the spin orientation of the M2 cell, the following assumptions were made: (i) The two magnetic structures are not phase-separated into domains, thus there are no M1 or M2 domains. (ii) The additional magnetic peaks that arise from the second magnetic transition do not change the M1
TABLE I. The magnetic structure of the M1 state with \(\Gamma_{1}\psi_{1}\). The Ni moment is \(1\mu_{B}\) per site.
| Ni site | \( m_{a} \) | \( m_{b} \) | \( m_{c} \) | \( m (\mu_{B}) \) |
| (0 0 0) | 0.569 | 0.569 | 0.569 | 0.986 |
| (0.5 0 0.5) | -0.569 | -0.569 | 0.569 | 0.986 |
| (0 0.5 0.5) | -0.569 | 0.569 | -0.569 | 0.986 |
| (0.5 0.5 0.5) | 0.569 | -0.569 | -0.569 | 0.986 |
TABLE II. The four domain structures of M2 corresponding to \(\Gamma_{1}\psi_{2}\), \(\Gamma_{1}\psi_{4}\), \(\Gamma_{3}\psi_{6}\), and \(\Gamma_{3}\psi_{8}\) (listed in that order).
| (a) Ni site | \( m_{a} \) | \( m_{b} \) | m_{c} | m (\mu_{B}) |
| (0 0 0) | -0.895 | 0.895 | 0.000 | 1.266 |
| (0.5 0 0.5) | 0.517 | -0.138 | 0.378 | 0.655 |
| (0 0.5 0.5) | -0 .138 | -0.517 | -0.378 | 0.655 |
| (0.5 0.5 0) | -0.517 | 0.517 | -1.033 | 1.266 |
| (0 0 0) | -0.138 | 0.517 | -0.378 | 0.655 |
| ( 0.5 0 0.5) | 0.517 | 0.517 | 1.033 | 1.266 |
| (0 0.5 0.5) | 0.895 | 0.895 | 0.000 | 1.266 |
| (0.5 0.5 0) | 0.517 | 0.138 | 0.378 | 0.655 |
| (0.0 0) | 0.517 | -0.138 | -0.378 | 0.655 |
| (0.5.0 0.5) | 0.895 | -0.895 | 0.000 | 1.266 |
| (0 0.5 0.5 0) | 0.138 | 0.517 | -0.378 | 0.655 0.655 |
| (0 0 0) | -0.517 | -0.517 | 1.033 | 1.266 |
| (0.5 0 0.5 0) | 0.138 | -0.517 | -0.378 | 0.655 |
| (0.5 0.5 0) | 0.517 0.517 | 0.138 | -0.378 | 0.655 |
| ( 0.0 0.0) | -0.895 | -0.895 | 0.000 | 1.266 1.266 |
magnetic structure. If the M2 magnetic structure had parallel components to the M1 structure, the M2 structure would change the M1 structure. However, the M1 and M2 magnetic structures are both AFM with different magnetic unit cells. This suggests that the M2 magnetic structure has to be orthogonal to the M1 magnetic structure at every Ni site. As shown in Fig. 4, the M1 and M2 magnetic peaks are separated from each other, and this will be used to explain the two magnetic transitions.
In the M1 phase, the \( \Gamma_{1}\psi_{1} \) representation with a propagation vector of \( k=(000) \) can reproduce the magnetic peaks with the proposed spin pattern shown in Fig. 5. Thus to find a candidate for the M2 magnetic structure, we consider all possible combinations of irreducible representations and basis vectors within \( Pa\bar{3} \) symmetry using the \( k=(\frac{1}{2}\frac{1}{2}\frac{1}{2}) \) vector. There are a total of 12 combinations of irreducible representations and basis vectors: \( \Gamma_{1} \) , \( \Gamma_{3} \) , \( \Gamma_{5} \) , and \( \psi_{1}-\psi_{12} \) . We introduce the following constraint because the M1 and M2 structures are normal to each other at every Ni site due to the second assumption stated above,
\[ 0=\mu_{M1,i}\cdot\mu_{M2,i} \quad (1) \]
In doing so, we can exclude \(\Gamma_{1}\psi_{1}\), \(\Gamma_{1}\psi_{3}\), \(\Gamma_{3}\psi_{5}\), and \(\Gamma_{3}\psi_{7}\). From the remaining combination of representations and basis vectors, \(\Gamma_{5}\psi_{9}-\Gamma_{5}\psi_{12}\) are excluded because they yield structures that have imaginary components, inconsistent with the simple antiferromagnetic structure observed in this system.
The remaining four candidates are all viable for the magnetic structure of the M2 phase. These are \( \Gamma_{1}\psi_{2} \) , \( \Gamma_{1}\psi_{4} \) , \( \Gamma_{3}\psi_{6} \) , and \( \Gamma_{3}\psi_{8} \) with refined spin configurations listed in Table II. Using one of the magnetic configurations, namely the \( \Gamma_{1}\Psi_{2} \) structure shown in Fig. 5(b), the magnetic peaks at \( (\frac{1}{2}\frac{1}{2}\frac{1}{2}) \) , and \( (\frac{1}{2}\frac{1}{2}\frac{3}{2}) \) can be reproduced as shown in Fig. 4 and also in the inset. At the same time, \( \Gamma_{1}\psi_{4} \) , \( \Gamma_{3} \psi_{6} \) , and \( \Gamma_{3} \psi_{8} \) can equally reproduce the given magnetic peaks. The R factor 21.75% is the same for all the suggested structures, and so is the
TABLE III. The magnetic structure of the combined M1 and M2 state with \(\Gamma_{1}\psi_{1}\) for M1 and \(\Gamma_{1}\psi_{2}\) for M2.
| Ni site | \( m_{a} \) | \( m_{b} \) | \( m_{c} \) | \( m (\mu_{B}) \) |
| S1( \( - \) + ) | -0.052 | -0.707 | 0.947 | 1.18 |
| S'1( \( - \) + ) | -0.707 | 0.052 | -0.947 | 1.18 |
| S2( \( - \) + ) | -0.431 | 1.086 | -0.191 | 1.18 |
| S'2( \( - \) + ) | -1.086 | -0.431 | 0.191 | 1.18 |
| L1( \( - \) + ) | -0.326 | 1.464 | 0.569 | 1.60 |
| L'1( \( + \) - ) | 1.464 | -0.326 | 0.569 | 1.60 |
| L2( \( + \) - ) | 0.052 | -0.052 | -1.602 | 1.60 |
| L'2( \( + \) - ) | 1.086 | -1.086 | 0.464 | 1.60 |
magnetic moment. These four magnetic structures correspond to four different domains.
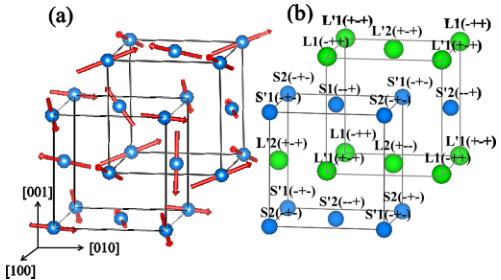
In Table III, a list of the magnetic moments per Ni site is provided for a magnetic structure that is constructed by combining the M1 and M2 phases using \( \Gamma_{1}\psi_{1} \) for M1 and \( \Gamma_{1}\psi_{2} \) for M2. Of the eight sites present in the unit cell, four of them have a small magnetic moment. These are designated by S and \( S' \) . The remaining four have a larger magnetic moment and are designated by L and \( L' \) . Because the differences are only plus or minus relative to the [100], [010], and [001] components of the Ni sites, the structures cannot be distinguished by neutron powder diffraction or by single-crystal neutron diffraction experiments. It is possible that all four magnetic structures form domains in \( NiS_{2} \) . The remaining combinations of \( M1\Gamma_{1}\psi_{1} \) with \( M2\Gamma_{1}\psi_{4} \) , \( \Gamma_{3}\psi_{6} \) , and \( \Gamma_{3}\psi_{8} \) are summarized in Table IV. In Fig. 6, the combined magnetic structure with \( M1\Gamma_{1}\psi_{1} \) and \( M2\Gamma_{1}\psi_{2} \) is depicted.
The determined magnetic moment in the M1 phase is \( 0.986\mu_{B} \) , while in the M2 phase the moment is either \( 0.655\mu_{B} \) or \( 1.266\mu_{B} \) at the four sites, as shown in Table II. Given that all the Ni magnetic sites follow the constraint, the magnetic moment at each site is simply calculated from \( \mu_{\mathrm{Ni}} = \sqrt{(\mu_{M1}^{2} + \mu_{M2}^{2})} \) . The Ni-S site moment is \( 1.18\mu_{B} \) ( \( M2 = 0.655\mu_{B} \) and \( M1 = 0.986\mu_{B} \) ) and the Ni-L site moment is \( 1.60\mu_{B} \) ( \( M2 = 1.266\mu_{B} \) and \( M1 = 0.986\mu_{B}) \) .
IV. MAGNETIC ANALYSIS OF \( NiS_{2-x}Se_{x} \)
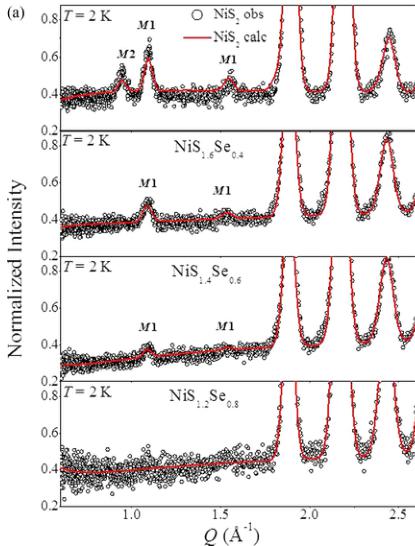
The magnetic structure was also investigated under doping of S with Se. The composition dependence of the diffraction pattern is shown in Fig. 7(a). All data were collected at
TABLE IV. The four possible magnetic domains of \( NiS_{2} \) . The \( M1\Gamma_{1}\psi_{1} \) is combined with the four possible M2 configurations.
| \( \Gamma_{1}\psi_{2(M2)} \) | \( \Gamma_{1}\psi_{4(M2)} \) | \( \Gamma_{3}\psi_{6(M2)} \) | \( \Gamma_{3}\psi_{8(M2)} \) | \( m(\mu_{B}) \) | |
| S1( \( - \) + ) | S1( \( + \) - ) | S1( \( ++ \) ) | S1( \( - \) + ) | 1.18 | |
| S'1( \( - \) + - ) | |||||
| S'2( \( - \) + - ) | S'1( \( ++ \) ) | S'1( \( - \) - ) | S'1( \( - \) + ) | 1.18 | 1.18 |
| S2( \( - \) + - ) | |||||
| S'2( $ - $ + - ) | S2( \( + \) + + ) | S2( \( - \) - + ) | S2( \( - \) - + ) | 1.18 | |
| L1( \( - \) + + ) | L1( \( + \) + - ) | L1( \( + \) - + ) | L1( \( - \) - ) | 1.60 | |
| L'1( \( + \) \( - \) + ) | L'1( \( - \) - ) | L'1( \( - \) + + ) | L'1( \( + \) + - ) | 1.60 | |
| L2( \( + \) - - ) | L2( \( - \) + - ) | L2( \( - \) + + ) | L2( \( + \) + + ) | 1.60 | |
| L'2( \( + \) \( - \) + ) | L'2( \( - \) - ) | L'2( \( - \) + + ) | L'2( \( + \) + - ) | 1.60 |

FIG. 6. (a) The combined spin structure of the M1 and M2 magnetic cells. The spin magnitude and direction are shown. In (b), the directions relative to the x, y, and z coordinates are shown for the large (L) and small (S) spins.
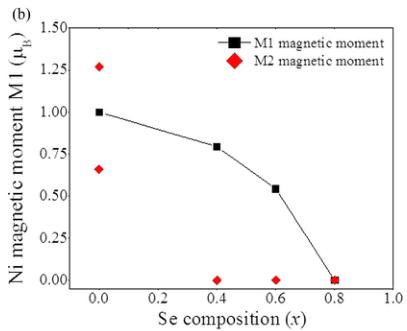
\(T=2\ \mathrm{K}\). Our results do not concur with previous phase diagrams [11]. As shown in Fig. 7(b), which is a plot of the magnetic moment as a function of doping, the \(M2\) structure disappears prior to \(x\sim0.4\). Therefore, the MIT does not coincide with the transition from the AFM insulating to AFM metallic state. It was previously proposed that the AFM insulating phase vanishes between \(x\sim0.45\) and \(0.5\). This contradicts our measurement, which shows that no \(M2\) peaks are observed at \(x=0.4\). Resistivity measurements on a single crystal (Ref. [12]) indicate that the MIT occurs at \(x=0.36\). This suggests that the disappearance of the insulating phase coincides with the disappearance of the \(M2\) magnetic phase. The metallic phase thus consists purely of the \(M1\) magnetic structure. By \(x=0.8\), magnetic order disappears. The moment is reduced as a function of doping, as shown in Fig. 5(b). Previous studies suggested that the antiferromagnetic metallic state extends up to \(x=1.0\) [11–14]. However, our neutron diffractograms show no evidence of magnetic peaks beyond \(x\lesssim0.8\).
Discussion
The magnetic structure of \( NiS_{2-x}Se_{x} \) was reexamined by neutron scattering using powder samples. Two consecutive magnetic transitions occur with decreasing temperature. At \( T_{N_{1}} = 39.2 \) K, the transition to the M1 magnetic structure with the \( k = (000) \) characteristic wave vector was confirmed, and the \( \Gamma_{1}\psi_{1} \) symmetry was determined. The magnetic moment is \( 0.986\mu_{B} \) . At \( T_{N_{2}} = 29.75 \) K, a second magnetic transition occurs to the M2 structure with a characteristic wave vector, \( k = (\frac{1}{2}\frac{1}{2}\frac{1}{2}) \) . Little was known about the nature of the second magnetic transition. Using magnetic point group theory, we determined that four magnetic domains are possible. The basic symmetry is that of \( \Gamma_{1}\psi_{2} \) with face-centered translations. Given that the M1 and M2 magnetic peaks coexist below \( T_{N_{2}} \) , the doubling of the unit cell in all three directions accommodates two Ni sites. With doping as in \( NiS_{2-x}Se_{x} \) , the M2 magnetic domains are quickly suppressed while the M1 structure remains even though the system has become metallic. As seen in Fig. 7(b), the magnetic moment is suppressed under doping and disappears altogether by x = 0.8. Why does magnetism persist in the metallic state?


FIG. 7. (a) The neutron diffraction pattern of \( NiS_{2-x}Se_{x} \) in the range of 0 < x < 0.8. By x = 0.8, no magnetic peaks are discernible. (b) The proposed magnetic phase diagram from the present results.
In this experiment, the \( (\frac{1}{2}00) \) magnetic peak reported in Ref. [5] was not observed in \( NiS_{2} \) . The \( (\frac{1}{2}\frac{1}{2}0) \) magnetic peak was not observed either. The proposed magnetic structures of \( NiS_{2} \) are compatible with this result. In addition, no continuous transitions are allowed for \( k = (\frac{1}{2}00) \) and \( (\frac{1}{2}\frac{1}{2}0) \) in the \( Pa\bar{3} \) symmetry based on Landau's theorem II [15,16]. There is no calculated neutron-scattering intensity from the proposed magnetic structure of \( NiS_{2} \) for these reflections either.
The \( (\frac{1}{2}\frac{1}{2}\frac{1}{2}) \) peak of the M2 phase has also been observed by synchrotron radiation diffraction, which implies that its origin is not purely magnetic [8]. Does the system undergo a structural transition? Some experiments seem to suggest that. For instance, the thermal expansion of a single crystal of \( NiS_{2} \) measured by the strain gauge method to estimate the crystal distortion indicates that the lattice contracts abruptly below \( T_{N_{2}} \) . This suggests that \( NiS_{2} \) undergoes a slight distortion from cubic symmetry below \( T_{N_{2}} \) that has been attributed to either an orthorhombic or a rhombohedral distortion [17]. However, none of the crystal structures that have rhombohedral or orthorhombic transitions can explain the appearance of the \( k = (\frac{1}{2}\frac{1}{2}\frac{1}{2})^{\prime} \) peak. It is possible that the reason the \( (\frac{1}{2}\frac{1}{2}\frac{1}{3})^{\prime} \) peak is observed by x-ray diffraction is that Ni actually has two charge sites that have different magnetic moments in the M2 structure. As was suggested in perovskite \( RNiO_{3} \) [18,19], it is possible that charge disproportionation of Ni occurs in \( NiS_{2} \) in the M2 phase. In \( NiS_{2} \) , the MIT can be explained by the disappearance of the charge disproportionation concomitant with the disappearance of the M2 structure at \( x \leqslant 0.4 \) .
The magnetic structure of \( NiS_{2} \) is similar to the magnetic structure of known antiferromagnets of MnO, FeO, CoO, and NiO [20] with dominant superexchange interactions. Antiferromagnetic domain walls have been reported in these systems, accompanied by a rhombohedral distortion [21,22]. Among them, the CoO is different where the magnetic structure has two magnetic propagation vectors that are \( k = (001) \) and \( k = (\frac{1}{2}\frac{1}{2}\frac{3}{2}) \) . The intensity of a \( (\frac{3}{2}\frac{3}{2}\frac{3}{2}) \) synchrotron x-ray peak in CoO is arguably too strong compared with that of the (001), implying that the origin of the \( (\frac{3}{2}\frac{3}{2}\frac{3}{3}) \) peak is a lattice modulation [23]. It has been proposed that charge disproportionation might be the case in this system as well. Thus the magnetic structure of CoO needs to be reexamined.
Previous studies argued for the presence of a weak ferromagnetic component along with the M2 phase [24]. It is puzzling to see how a simple binary compound can demonstrate such a complex magnetic state. The four determined magnetic structures, although complex, cancel out in total. Thus there is no weak ferromagnetic component in this model, nor should it exist based on the \( Pa\bar{3} \) symmetry from the magnetic point group theory analysis. At the same time, along the a axis, the spin components do not cancel out in the planes with all S spins and all L spins even though they cancel out in total. Thus a slight change of the magnetic structure can cause a weak ferromagnetic component. Therefore, the key to differentiating between the four magnetic structures may involve looking at spin waves.
ACKNOWLEDGMENTS
The authors would like to acknowledge J. C. Neuefeind and M. Feygenson for their help during the NOMAD measurement. They would like to thank J. Gardner for fruitful discussions, and L. Peng and M. Grayson for the transport measurements on the x = 0.6 and 0.8 compositions. This work has been
supported by the Department of Energy, Grant No. DEFG02-01ER45927. Work at Argonne National Laboratory was supported by the U.S. Department of Energy, Office of Science, Materials Sciences and Engineering. Work at
[1] M. Imada, A. Fujimori, and Y. Tokura, Rev. Mod. Phys. 70, 1039 (1998).
[2] C. Schuster, M. Gatti, and A. Rubio, Eur. Phys. J. B 85, 325 (2012).
[3] J. Kunes, L. Baldassarre, B. Schachner, K. Rabia, C. A. Kuntscher, D. M. Korotin, V. I. Anisimov, J. A. McLeod, E. Z. Kurmaev, and A. Moewes, Phys. Rev. B 81, 035122 (2010).
[4] K. Kikuchi, T. Miyadai, T. Fukui, H. Ito, and K. Takizawa, J. Phys. Soc. Jpn. 44, 410 (1978).
[5] T. Thio, J. W. Bennett, and T. R. Thurston, Phys. Rev. B 52, 3555 (1995).
[6] Y. Nishihara, S. Ogawa, and S. Waki, J. Phys. Soc. Jpn. 39, 63 (1975).
[7] T. Miyadai, S. Sudo, Y. Tazuke, N. Mōri, and Y. Miyako, J. Magn. Magn. Mater. 31–34, 337 (1983).
[8] Y. Feng, R. Jaramillo, A. Banerjee, J. M. Honig, and T. F. Rosenbaum, Phys. Rev. B 83, 035106 (2011).
[9] J. Neuefeind, M. Feygenson, J. Carruth, R. Hoffmann, and K. K. Chipley, Nucl. Instrum. Methods Phys. Res., Sect. B 287, 68 (2012).
[10] A. S. Wills, Physica B 276, 680 (2000).
[11] P. G. Niklowitz, P. L. Alireza, M. J. Steiner, G. G. Lonzarich, D. Braithwaite, G. Knebel, J. Flouquet, and J. A. Wilson, Phys. Rev. B 77, 115135 (2008).
Northwestern University was supported in part by the NSF MRSEC program DMR-121262 at the Materials Research Science and Engineering Center of Northwestern University, and a McCormick Research Catalyst Award.
[12] M. Matsuura, H. Hiraka, K. Yamada, and Y. Endoh, J. Phys. Soc. Jpn. 69, 1503 (2000).
[13] H. Takano and A. Okiji, J. Phys. Soc. Jpn. 50, 3835 (1981).
[14] X. Yao, J. M. Honig, T. Hogan, C. Kannewurf, and J. Spalek, Phys. Rev. B 54, 17469 (1996).
[15] L. D. Landau and E. M. Lifshitz, in Statistical Physics (Pergamon, London, 1958).
[16] A. P. Cracknell, in Magnetism in Crystalline Materials (Pergamon, London, 1958), Vol. 72, p. 89.
[17] H. Nagata, H. Ito, and T. Miyadai, J. Phys. Soc. Jpn. 41, 2133 (1976).
[18] J. A. Alonso, J. L. Garcia-Munoz, M. T. Fernandez-Diaz, M. A. G. Aranda, M. J. Martinez-Lope, and M. T. Casais, Phys. Rev. Lett. 82, 3871 (1999).
[19] J. A. Alonso, M. J. Martinez-Lope, M. T. Casais, J. L. Garcia-Munoz, and M. T. Fernandez-Diaz, Phys. Rev. B 61, 1756 (2000).
[20] W. L. Roth, Phys. Rev. 110, 1333 (1958).
[21] B. van Laar, Phys. Rev. 138, A584 (1965).
[22] T. Yamada, J. Phys. Soc. Jpn. 21, 664 (1966).
[23] K. Tomiyasu, T. Inami, and N. Ikeda, Phys. Rev. B 70, 184411 (2004).
[24] T. Higo and S. Nakatsuji, J. Phys. Soc. Jpn. 84, 053702 (2015).