| Transition Temperature | 47 K |
|---|---|
| Experiment Temperature | 10 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Pnma (#62) |
| Magnetic Space Group | P21/c' (#14.78) |
| Magnetic Point Group | 2/m' (5.4.15) |
| Lattice Parameters | 10.3377 6.0112 4.6950 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1103/physrevb.92.024404 |
| Reference | R. Toft-Petersen, M. Reehuis, T.B.S. Jensen, N.H. Andersen, J. Li, M.D. Le, M. Laver, C. Niedermayer, B. Klemke, K. Lefmann and D. Vaknin, Physical Review B (2015) 92. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Fe1 | Fe | -0.067 | 4.09 | -0.063 | 4.09 |
Anomalous magnetic structure and spin dynamics in magnetoelectric LiFePO_{4}
Rasmus Toft-Petersen, \( ^{1,*} \) Manfred Reehuis, \( ^{1} \) Thomas B. S. Jensen, \( ^{2} \) Niels H. Andersen, \( ^{2} \) Jiying Li, \( ^{3} \) Manh Duc Le, \( ^{1,4} \)
Mark Laver, \( ^{2,5,6} \) Christof Niedermayer, \( ^{5} \) Bastian Klemke, \( ^{1} \) Kim Lefmann, \( ^{7} \) and David Vaknin \( ^{3} \)
\( ^{1} \) Helmholtz-Zentrum Berlin für Materialien und Energie, D-14109 Berlin, Germany
\( ^{2} \) Department of Physics, Technical University of Denmark, DK-2800 Kgs. Lyngby, Denmark
\( ^{3} \) Ames Laboratory and Department of Physics and Astronomy, Iowa State University, Ames, Iowa 50011, USA
\( ^{4} \) Center for Correlated Electron Systems, Institute for Basic Science (IBS), Seoul 151-747, Korea
\( ^{5} \) Laboratory for Neutron Scattering and Imaging, Paul Scherrer Institut, CH-5232 Villigen, Switzerland
\( ^{6} \) Department of Metallurgy and Materials, University of Birmingham, Birmingham B15 2TT, United Kingdom
\( ^{7} \) Nanoscience Center, Niels Bohr Institute, University of Copenhagen, DK-2100 Copenhagen, Denmark
(Received 25 April 2015; published 6 July 2015)
We report significant details of the magnetic structure and spin dynamics of \( LiFePO_{4} \) obtained by single-crystal neutron scattering. Our results confirm a previously reported collinear rotation of the spins away from the principal b axis, and they determine that the rotation is toward the a axis. In addition, we find a significant spin-canting component along c. The possible causes of these components are discussed, and their significance for the magnetoelectric effect is analyzed. Inelastic neutron scattering along the three principal directions reveals a highly anisotropic hard plane consistent with earlier susceptibility measurements. Using a spin Hamiltonian, we show that the spin dimensionality is intermediate between XY- and Ising-like, with an easy b axis and a hard c axis. It is shown that both next-nearest neighbor exchange couplings in the bc plane are in competition with the strongest nearest neighbor coupling.
DOI: 10.1103/PhysRevB.92.024404
I. INTRODUCTION
In the past decade, there has been a notable upswing in the investigation of multiferroic materials that simultaneously exhibit multiple ferroic order parameters \( [1,2] \) . The magnetoelectric (ME) materials, where such coexisting order parameters couple ferroelectricity with magnetization, have also experienced a revival of interest due to the scientific challenges to unravel the coupling mechanism \( [2,3] \) , as well as for their potential applications \( [4] \) . The lithium-ortho-phosphates group \( \mathrm{LiMOPO}_{4} \) (M = Mn, Co, Fe, or Ni) all exhibit a ME effect in their low-temperature antiferromagnetic (AFM) phases \( [5] \) . In addition, both \( \mathrm{LiMnPO}_{4} \) \( [6] \) and especially \( \mathrm{LiFePO}_{4} \) \( [7] \) have been proposed and used as materials for lithium battery cathodes, \( \mathrm{LiFePO}_{4} \) finding current commercial value \( [8] \) . Just recently, a graphene-modified \( \mathrm{LiFePO}_{4} \) cathode has been shown to have a drastically increased specific capacity \( [9] \) .
Spin-orbit coupling is emerging as a significant ingredient of the ME coupling in general and in the lithium-orthophosphates in particular \( [10–12] \) . In fact, the relative strength of the ME effect in these transition-metal-based compounds seems to scale with the effective total orbital contribution also affecting the single-ion anisotropy and the effective g factor. For instance, \( LiMnPO_{4} \) , where the magnetic \( Mn^{2+} \) ion has L=0 by Hund's rules, has a very small but finite higher-order orbital contribution \( [12] \) ( \( \Delta g/g \rightarrow 0 \) ) and displays the weakest ME effect among its counterparts \( [5] \) . By contrast, \( LiCoPO_{4} \) (L=3) has very significant orbital contributions with \( \Delta g/g \approx 0.3 \) and large single-ion anisotropy \( [13–15] \) and exhibits a 40 times stronger ME coupling than that of \( LiMnPO_{4} \) \( [5,16,17] \) . Intermediate in coupling strength are \( LiFePO_{4} \) and \( LiNiPO_{4} \) ( \( \Delta g/g \approx 0.1 \) ) \( [10] \) . The zero-field magnetic structure of the four magnetic ions in \( LiNiPO_{4} \) is
PACS number(s): 75.50.−y, 75.85.+.t, 28.20.Cz
predominantly polarized along c but also slightly canted along a due to the Dzyaloshinsky-Moriya (DM) interaction. It has been shown that the ME effect in \( LiNiPO_{4} \) can be explained as resulting from enhanced spin-canting that is induced by an applied magnetic field [10]. In \( LiCoPO_{4} \) and \( LiFePO_{4} \) , a similar microscopic ME mechanism is impossible since the spin polarization is along the crystallographic b axis [18,19], perpendicular to which the Pnma symmetry prevents spin components along a and c. However, collinear rotations of the magnetic moments away from the b axis have recently been found in both compounds [20,21]. Such rotations suggest that the crystal structure symmetry is most likely lower than orthorhombic Pnma at \( T_{N} \) . In addition, such a spin rotation can produce ferrotoroidicity [22] as observed in \( LiCoPO_{4} \) [23]. Similarly, ferrotoroidicity should also be present in \( LiFePO_{4} \) , the sign of which depends on the rotation of the magnetic moments [24]. Here, we report on the exact polarization of this additional spin component and an observed zero-field spin canting in \( LiFePO_{4} \) . Although these additional spin components are minor, they are shown in this work to enable a magnetoelectric response via the DM interaction.
Spin waves obtained by inelastic neutron scattering (INS) experiments have shown magnetic frustration due to competing exchange couplings in all known lithium orthophosphates \( [14,20,25,26] \) . For \( LiNiPO_{4} \) , the magnetic frustration with local XY anisotropy promotes a rich phase diagram including an elliptical and canted spin spiral state at low temperatures \( [10,17,27,28] \) . In \( LiFePO_{4} \) , previous INS measurements reported only one excitation branch \( [20] \) that suggested an isotropic hard plane using a spin Hamiltonian with an Ising-like anisotropy \( [20] \) . This is not entirely compatible with subsequent susceptibility measurements showing an anisotropic hard plane \( [29] \) . In addition, the spin-wave model used for \( LiFePO_{4} \) in previous studies \( [20] \) assumed only one next-nearest-neighbor (NNN) interaction along the c axis and one out-of-plane. Theoretical calculations \( [30] \) and
TABLE I. Crystal structure parameters of \( LiFePO_{4} \) obtained from refinement of single-crystal diffraction data ( \( \lambda = 0.89 \, \AA \) ) collected at room temperature using the Pnma space group. The thermal parameters \( U_{ij} \) (given in \( 100 \, \AA^{2} \) ) are in the form \( \exp\left[-2\pi(U_{11}h^{2}a^{*2} + \cdots + 2U_{13}hla^{*}c^{*})\right] \) . For symmetry reasons, the values \( U_{12} \) and \( U_{23} \) of the atoms located at the Wyckoff position \( 4c \) are equal to zero for the space group Pnma. \( a = 10.3377(10) \, \AA \) , \( b = 6.0112(10) \, \AA \) , \( c = 4.6950(10) \, \AA \) , \( V = 291.76(8) \, \AA^{3} \) .
| Atom | Site | x | y | z | U11 | U22 | U33 | U12 | U13 | U23 | Occ. | |
| Li | 4a | 0 | 0 | 0 | 2.18(12) | 1.79(13) | 1.14(11) | 0.00(11) | 0.00(7) | -0.45(10) | 1.011(22) | |
| Fe | 4c | 0.28197(4) | 1/4 | 0.97484(9) | 0.49(2) | 0.51(2) | 0.67(2) | 0 | 0.01(1) | 0 | 1 | |
| P | 4c | 0.09483(7) | 1/4 | 0.41813(15) | 0.43(3) | 0.50(3) | 0.35(3) | 0 | 0.01(1) | 0 | 1 | |
| O1 | 4c | 0.09697(7) | 1/4 | 0.74224(15) | 0.82(3) | 0.92(3) | 0.39(2) | 0 | 0.04(2) | 0 | 1.006(7) | |
| O2 | 4c | 0.45711(7) | 1/4 | 0.20581(15) | 0.51(3) | 0.88(3) | 0.65(3) | 0 | 0.05(2) | 0 | 1.007(6) | |
| O3 | 8d | 0.16568(5) | 0.04642(9) | 0.28465(11) | 0.91(2) | 0.67(2) | 0.67(2) | 0.25(1) | 0.11(1) | 0.07(1) | 0.993(5) |
experimental results indicate that five exchange parameters are non-negligible. The dispersion of the magnetic excitations along 00L had not been measured yet in \( LiFePO_{4} \) , making a concise evaluation of the degree of frustration in the bc plane difficult. In the present work, we address these issues using elastic and inelastic neutron scattering to establish a more complete spin Hamiltonian for \( LiFePO_{4} \) .
II. EXPERIMENTAL DETAILS
High-quality \( LiFePO_{4} \) single crystals were grown by the standard flux growth technique [31]. The experimental purity and stoichiometry were confirmed by laboratory x-ray powder diffraction. A 0.35 g crystal nearly spherical in shape was used in all neutron experiments. Diffraction measurements were performed on the RITA-II triple-axis spectrometer at the SINQ, Paul Scherrer Institute, Switzerland—using a wavelength of \( \lambda = 4.04 \) Å and with the sample placed in an ILL orange cryostat. Diffraction data were collected on the four-circle diffractometer E5 at the BER II reactor of the Helmholtz Zentrum Berlin (HZB). At 300 K, we collected a full dataset with \( \lambda = 0.89 \) Å using a copper monochromator and an Er filter. For the magnetic reflections below \( T_{N} = 50 \) K, we collected data sets at 10 K and 100 K using a PG monochromator with \( \lambda = 2.38 \) Å and a PG filter. For the low-temperature measurements, we used a closed-cycle cryostat with a base temperature of 10 K. For a refinement of the crystal and magnetic structures, the program FULLPROF (Refs. [32,33]) was used with nuclear scattering lengths \( b(\mathrm{Li}) = -1.90 \) fm, \( b(\mathrm{O}) = 5.805 \) fm, \( b(\mathrm{P}) = 5.13 \) fm, and \( b(\mathrm{Fe}) = 9.54 \) fm [34]. The magnetic form factor of the \( Fe^{2+} \) ion was taken from Ref. [35]. To determine the absolute value of the magnetic moments, we have refined the overall scale factor and extinction parameter from crystal structure refinements using the data collected at 300 K, well above the Néel temperature \( T_{N} = 47(3) \) K. With the absorption and extinction corrected magnetic structure factors, we were able to obtain the magnetic moments of the iron atoms in the magnetically ordered state.
The INS measurements were performed on the newly upgraded FLEXX spectrometer at the HZB [36] (constant final energy with \( \lambda_{f}=4.05 \) Å). All the inelastic measurements were performed at 1.7 K using a standard ILL orange cryostat.
For heat-capacity measurements, we used a 6.5 mg \( LiFePO_{4} \) single crystal of the same batch as the one used for neutron scattering. The measurements were done in zero field, using a Physical Property Measurement System (PPMS, Quantum Design) at the Laboratory for Magnetic Measurements, HZB.
III. RESULTS AND DISCUSSION
A. Crystal structure
In earlier works, the crystal structure of \( LiFePO_{4} \) was described in the orthorhombic space group \( P_{nma} \) (No. 62) [37,38]. This space-group symmetry could be confirmed from our analysis [39] of the dataset collected at room temperature. The Li and O3 atoms are located at the Wyckoff positions \( 4a(0,0,0) \) and \( 8c(x,y,z) \) , while all the other atoms—Fe, P, O1, and O2—are located at the position \( 4c(x,1/4,z) \) . A full dataset of 3095 reflections (820 unique) was collected at 300 K using a neutron wavelength \( \lambda = 0.89 \) Å. The refinements of a total of 41 parameters (the overall scale and extinction factor g, 11 positional, and 28 anisotropic thermal parameters) resulted in a residual \( R_{F} = 0.039 \) (defined as \( R_{F} = \sum ||F_{obs}| - |F_{calc}||/\sum |F_{obs}| \) ). For the secondary extinction parameter g, which is related to a Gaussian mosaic distribution, we obtained the value \( g = 921(32) \) rad \( ^{-1} \) , resulting in a maximum extinction of 54% (in F) for the strongest Bragg reflection. The g value reveals a peak shape with a full width at half-maximum (FWHM) of 2.48 min of arc. In the final refinement, we also have the occupancies of the Li and O atoms as free parameters. In Table I, where the results of the refinements are summarized, it can be seen that the atomic positions of both the Li and O atoms are fully occupied.
B. Magnetic structure
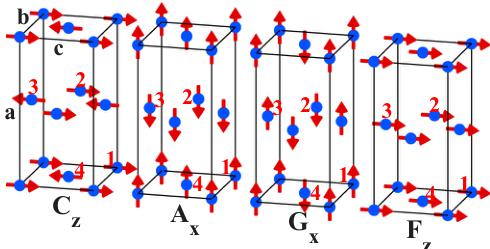
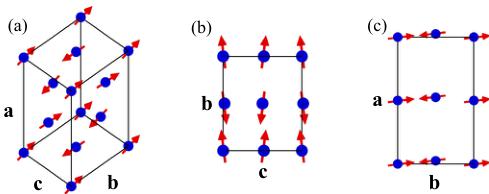
Possible magnetic structures of the sublattice in \( LiFePO_{4} \) were deduced from representation analysis [39] using the orthorhombic space group \( P_{nma} \) and the propagation vector \( k = 0 \) [40,41]. The four magnetic \( Fe^{2+} \) ions are located on the Wyckoff position 4c: \( \mathbf{r}_{1} = (1/4 + x, 1/4, -z) \) , \( \mathbf{r}_{2} = (3/4 + x, 1/4, 1/2 + z) \) , \( \mathbf{r}_{3} = (3/4 - x, 3/4, z) \) , and \( \mathbf{r}_{4} = (1/4 - x, 3/4, 1/2 - z) \) , where x = 0.03 and z = 0.025 in the orthorhombic unit cell. We have used the notation given in Refs. [10,27], denoting the four irreducible basis vectors \( A(+ - - +) \) , \( G(+ - + -) \) , \( C(+ + - -) \) , and \( F(+ + + +) \) , where the brackets show the relative phase factors of the spins on the sites \( (\mathbf{r}_{1}, \mathbf{r}_{2}, \mathbf{r}_{3}, \mathbf{r}_{4}) \) . The eight irreducible representations of the \( P_{nma} \) space group are given in Table II, and examples of each symmetry class are shown in Fig. 1.
TABLE II. Irreducible representations of the Pnma space group generated for the Wyckoff position 4c.
| P_{nma} | \( \Gamma_{1} \) | \( \Gamma_{2} \) | \( \Gamma_{3} \) | \( \Gamma_{4} \) | \( \Gamma_{5} \) | \( \Gamma_{6} \) | \( \Gamma_{7} \) | \( \Gamma_{8} \) |
| x | \( F_{x} \) | \( G_{x} \) | \( C_{x} \) | \( A_{x} \) | ||||
| y | \( G_{y} \) | \( F_{y} \) | \( A_{y} \) | \( C_{y} \) | ||||
| z | \( G_{z} \) | \( F_{z} \) | \( A_{z} \) | \( C_{z} \) |
The intensity of magnetic Bragg scattering at any given point in reciprocal space is proportional to the magnetic neutron scattering cross section, which is proportional to \( |F_{R}(\mathbf{Q})|^{2}|P(\mathbf{Q})|^{2} \) for a collinear structural component, where the structure factor \( (F) \) and polarization \( (P) \) factors are given by
\[ F_{R}(\mathbf{Q})=\sum_{d}\mathbf{m}_{d}^{R}e^{i\mathbf{Q}\cdot\mathbf{r}_{d}},\quad\mathbf{P}(\mathbf{Q})=\hat{\mathbf{Q}}\times(\hat{\mathbf{e}}\times\hat{\mathbf{Q}}). \quad (1) \]
Here \( m_{d}^{R} \) is the magnetic moment of the ion at site \( d = 1, \ldots, 4 \) in the irreducible basis vector \( R = C, A, G, and F \) , \( \hat{Q} \) is the unit vector along the neutron momentum transfer, and \( \hat{e} \) is the unit vector along \( m_{d}^{R} \) . Table III lists \( |F_{R}(\mathbf{Q})|^{2} \) (normalized to unit magnetic moment) and \( |P(\mathbf{Q})|^{2} \) for R and all spin directions \( \hat{e} \) parallel to x, y, or z for four fundamental magnetic Bragg peaks, for which the temperature dependence using the E5 four-circle diffractometer is presented below. The numbers in Table III represent the sensitivity of each peak to the different magnetic structures.
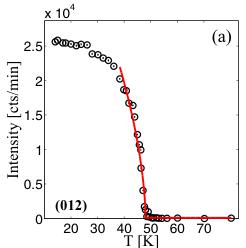
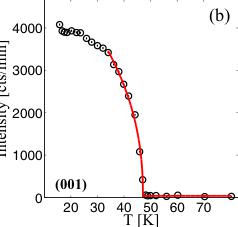
In agreement with Rousse et al. [40], strong magnetic intensities were found for the 101 and 210 reflections confirming the dominant C-type structure component along the y direction. This ordering corresponds to the representation \( \Gamma_{8}=[0,C_{y},0] \) given in Table II. For this magnetic structure, some magnetic reflections overlap with allowed nuclear peaks. The refinements of the crystal structure (above \( T_{N} \) ) show a pronounced extinction effect, which manifests itself by a substantial reduction of the strongest observed \( F^{2} \) values as compared to the calculated values. Therefore, the very strong 101 and 210 peaks have been left out of the final refinement. For tracking the order parameter, we monitored the structurally forbidden 001 and 012 magnetic reflections as a function of temperature (Fig. 2). The fit to the intensity versus temperature using a power law yields a Néel temperature

FIG. 1. (Color online) Irreducible basis vectors of LiFePO₄ using the Pnma space group. Only the sublattice of magnetic ions is shown.
TABLE III. Squared structure factors ( \( F^{2} \) ) and polarization factors ( \( P^{2} \) ) for the main peaks reflecting the three observed components of the magnetic structure.
| hkl | \( F_{C}^{2} \) | \( F_{A}^{2} \) | \( F_{G}^{2} \) | \( F_{F}^{2} \) | \( P_{x}^{2} \) | \( P_{y}^{2} \) | \( P_{z}^{2} \) | \( I_{\text{corr}} \) |
| 012 | 14 | 0 | 2 | 0 | 1 | 0.86 | 0.14 | 5.3 |
| 001 | 0.5 | 0 | 15.5 | 0 | 1 | 1 | 0 | 0.46 |
| 100 | 0 | 15.4 | 0.6 | 0 | 0 | 1 | 1 | 0.0043 |
| 010 | 16 | 0 | 0 | 0 | 1 | 0 | 1 | 0.0044 |
of \( T_{N} = 47.0(1) \) K. This is smaller than previously reported values [18,20] but is most likely due to a temperature gradient in our cryostat setup, since \( T_{N} = 50.0(1) \) K was measured using the same sample in the RITA-II experiment, where the presence of exchange gas reduces such temperature gradients. Due to the presence of strong extinction and a significant temperature gradient in the sample mount, the critical exponent is not subject to interpretation in this work. The overall scale factor and the extinction parameter were taken from the crystal structure refinement at 300 K, and fixed for the refinement of the magnetic structure. In fact, for the reflections 001 and 012, we could obtain a satisfactory agreement between the observed and calculated \( F^{2} \) values resulting in a residual \( R(F^{2}) = 0.049 \) . The refined magnetic moment \( \mu_{y} = 4.09(4)\mu_{B} \) ( \( C_{y} \) component) is in good agreement with the moment value \( \mu_{y} = 4.19(5)\mu_{B} \) obtained earlier from neutron powder data [40]. Interestingly, the magnetic reflection 001 could not be observed in the neutron powder pattern reported by Rousse et al. [40], but in the present single-crystal work, this reflection is quite strong, as shown in Fig. 2. In fact, a simulation of a powder pattern using the C-type ordering could not generate significant intensity at the position of the 001 reflection. Thus, it is clearly evident that single-crystal diffraction reveals more structural details than neutron powder diffraction. As a consequence, the pronounced extinction leads to a significant decrease of the strong magnetic reflection 012 leading to a much reduced ratio \( F^{2}(012)/F^{2}(001) \) in comparison to the powder data.
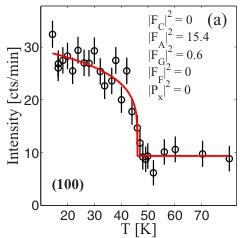
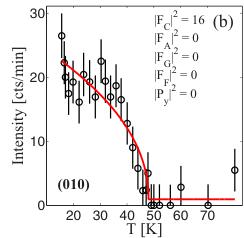
Figure 3 shows the temperature dependence of the 100 and 010 integrated intensities as a function of temperature with a transition temperature in agreement with \( T_{N} \) . Both the 100 and 010 peaks are not allowed by the \( C_{y} \) -type structure.


FIG. 2. (Color online) Temperature dependence of the two magnetic peaks 012 (a) and 001 (b). The red lines represent a power-law fit as a guide to the eye.


FIG. 3. (Color online) The intensity of the 100 peak reflecting the \( A_{z} \) component (a) and the 010 peak reflecting the \( C_{x} \) component. The integrated intensities of the magnetic scattering have similar values. The red lines represent a power-law fit as a guide to the eye.
In Refs. [20,21], magnetic intensity was found in the 010 reflection in \( LiFePO_{4} \) and \( LiCoPO_{4} \) , respectively. This was interpreted in terms of a collinear rotation of the spins away from the high-symmetry b axis. These experiments were conducted on a triple-axis spectrometer and confined to one scattering plane, and therefore without completely establishing the direction of the rotation or the detailed magnetic structure since this was the only deviant peak reported. The 010 reflection solely reflects \( C_{x} \) and \( C_{z} \) structure components due to the structure and polarization factors. Here, we find weak magnetic intensity in the 010 reflection, but also in the 100 peak mainly reflecting \( A_{z} \) and \( A_{y} \) components (see Fig. 3). Since the intensities of the two deviant magnetic peaks are similar, and since \( C_{x} \) and \( A_{z} \) belong to the same irreducible representation, the simplest interpretation is that the structure is described by the vector \( [C_{x}, C_{y}, A_{z}] \) , which expressed in terms of irreducible representations is \( \Gamma_{5} \oplus \Gamma_{8} \) . Thus, the magnetic structure has two deviant features, a collinear rotation of the spins toward the a axis and a spin canting along the c axis. The refined spin rotation and canting moments are \( \mu_{x} = 0.067(5)\mu_{B} \) and \( \mu_{z} = 0.063(5)\mu_{B} \) along a and c, respectively, corresponding to an overall rotation of the ordered moments of \( 1.3(1)^{\circ} \) off the b axis (see Fig. 4).
C. Crystal symmetry
The additional magnetic structure components in \( LiFePO_{4} \) have a nontrivial origin. Any term in the Hamiltonian quadratic in spin that would couple the main \( C_{y} \) structure to any of the canting components ( \( A_{i} \) or \( G_{i} \) ) cannot be invariant with respect

FIG. 4. (Color online) The magnetic structure of \( LiFePO_{4} \) (a) and the projections onto the bc plane (b) and ab plane (c), respectively. The canting and rotation angles have been exaggerated for clarity.

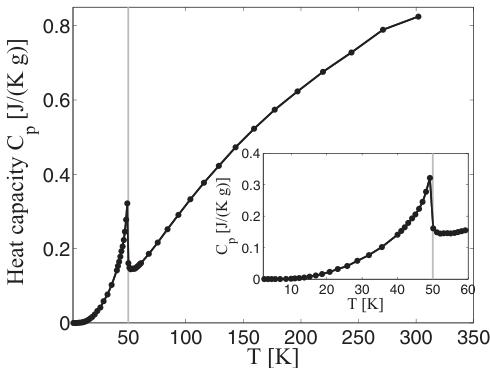
FIG. 5. The heat capacity of \( LiFePO_{4} \) vs temperature at zero magnetic field. The magnetic phase transition is clearly evident at 50 K, and no sign of a structural phase transition is evident between 50 and 300 K. The statistical errors are smaller than the marker size, but there can be a systematic error of up to 5% in the \( C_{p} \) measurements.
to all of the P_nma symmetries describing the crystal structure of \( LiFePO_{4} \) . This is due to the fact that the irreducible basis vector describing the main magnetic structure, \( C_{y} \) , is the only basis vector in its irreducible representation, \( \Gamma_{8} \) . It is interesting to note that a DM term of the form \( \mathcal{H}_{DM} = S_{1}^{z}S_{4}^{x} - S_{1}^{x}S_{4}^{z} + S_{3}^{z}S_{2}^{x} - S_{3}^{x}S_{2}^{z} \) is allowed by P_nma symmetry [10] and couples \( A_{z} \) with \( C_{x} \) components to make them energetically favourable. But even the existence of such a term in \( LiFePO_{4} \) cannot, within the Landau theory of second-order phase transitions, lift the requirement that only order parameters belonging to a single irreducible representation can become critical at each transition. The observation in this work of order parameters from two irreducible representation implies that either another second-order phase transition is present, or that the ordering transition is first-order. From the data presented here, it is obvious that all three structure components (i.e., the magnetic peaks 010, 100, and 012) represent conventional second-order phase transitions with the same ordering temperature. The most probable cause of the observed magnetic structure in \( LiFePO_{4} \) is therefore that the structure is not P_nma at \( T_{N} \) . As an additional examination of whether a structural transition takes place below 300 K, we have measured the heat capacity of a 6.5 mg \( LiFePO_{4} \) single crystal. It is evident that the antiferromagnetic ordering transition is the only one below 300 K, as shown in Fig. 5.
Therefore, if the crystal structure has a lower symmetry than Pnma at all temperatures, the deviation must be small enough not to be readily observed in this study as well as the many previous room-temperature x-ray and neutron powder experiments [18,40,42,43]. There was no anomaly in the thermal variation of the strongest nuclear peaks between 10 and 100 K. These peaks have pronounced extinction, and a structural phase transition could cause a change in the degree of extinction, which could result in a strong change in intensity as observed earlier for \( YVO_{3} \) in Ref. [44], where the crystal structure changes from orthorhombic to
monoclinic. It is possible that there is a small structural distortion, inherent and thus present at all temperatures. The corresponding lowering of the structural symmetry could result in \( C_{y} \) , \( C_{x} \) , and \( A_{z} \) belonging to the same irreducible representation and hence the same order parameter. This could also allow large enough DM or anisotropic exchange terms to generate the observed magnetic structure. Such a strong impact of minor structural details on the magnetic interactions (and hence the magnetic structure) are naturally very relevant for a microscopic explanation of the ME effect. These structural details could be resolved in high-resolution synchrotron x-ray experiments.
D. Implications for the magnetoelectric effect
The existence and strength of DM terms depend entirely on the symmetry of the crystal lattice and the significance of the spin-orbit coupling, respectively [45]. In crystal fields of low symmetry such as \( LiFePO_{4} \) , the spin-orbit coupling can restore some orbital momentum to the otherwise quenched ground state and produce large anisotropies in the g tensor as reported for \( LiFePO_{4} \) in Refs. [29,46]. This orbital contribution to the magnetization can produce ME effects even in the absence of spin canting. In Ref. [11], it was calculated ab initio that the polar distortions created by an applied electrical field can cause an ME response in \( LiFePO_{4} \) by virtue of orbital magnetization. However, another route to a ME response is possible via the magnetic interactions between the \( Fe^{2+} \) ions. If the magnetic ground state contains a significant orbital contribution, a change in the crystal structure creating an electric polarization can have a strong impact on the DM terms, and vice versa. Thus, lowering the crystal symmetry by allowing for an electric polarization, the magnetic energy can be minimized via the DM terms, as the field-induced change in spin canting changes the DM energy of the system. For fields applied along the spins in a collinear antiferromagnet, the DM energy is unchanged since all spins are either parallel or antiparallel. However, the observation of the anomalous \( A_{z} \) and \( C_{x} \) components makes both a superexchange- and DM-mediated mechanism for the ME effect possible.
1. Field applied along b
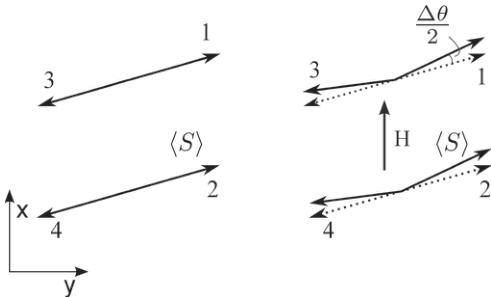
In Ref. [10], a mechanism for the ME effect for \( LiNiPO_{4} \) was proposed, facilitated by the asymmetry in the canting angles of spin pairs (1, 2) and (3, 4), induced by the applied field. This causes a difference in the superexchange energy between the two spin pairs leading to the ME effect. In \( LiFePO_{4} \) , due to the observed spin canting, a similar term is possible via the DM interaction for fields applied along b, where a similar asymmetry in canting angle occurs as shown in Fig. 6. For this purpose, the relevant DM interaction allowed by Pnma symmetry is
\[ \mathcal{H}_{\mathrm{D M}}=D_{12}^{y}\big(S_{1}^{z}S_{2}^{z}-S_{1}^{x}S_{2}^{z}\big)+D_{34}^{y}\big(S_{3}^{z}S_{4}^{x}-S_{3}^{x}S_{4}^{z}\big), \quad (2) \]
where \( P_{nma} \) requires \( D_{12}^{y}=D_{34}^{y} \) . The observed minor structural components \( A_{z} \) and \( C_{x} \) of equal magnitude minimizes such a term. The magnitudes of these components correspond to an overall rotation of all spins by \( \theta_{c}=1.3^{\circ} \) away from the b axis.

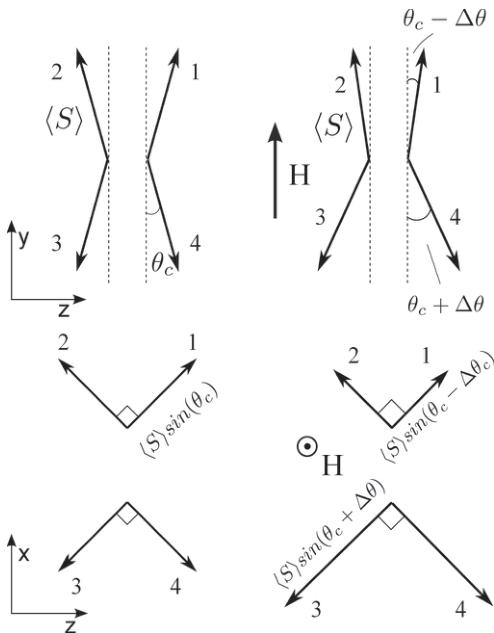
FIG. 6. The magnetic structure in fields applied along b. The small field-induced difference in canting angle between the two spin pairs (1,2) and (3,4) is evident. This corresponds to a difference in the magnitude of the \( A_{z} \) and \( C_{x} \) components in the ac plane.
For small fields along b, the system accommodates the Zeeman term by aligning spins (1, 2) along the field and rotating spins (3, 4) away from the b axis as shown on Fig. 6, with no change in anisotropy energy for small angles. The components in the ac plane of spins 1 (3) and 2 (4) are perpendicular and have magnitude proportional to \( \langle S\rangle\sin(\theta_{c}\pm\Delta\theta)\approx\langle S\rangle(\theta_{c}\pm\Delta\theta) \) for small angles. Here \( \Delta\theta \) is the angular deviation from \( \theta_{c} \) in applied fields. The field-induced change in DM energy described by Eq. (2) can be written as
\[ \begin{align*}\Delta E_{\mathrm{DM}}^{P||x}\\=\langle S\rangle^{2}\big(D_{12}^{y}+D_{34}^{y}\big)\Delta\theta^{2}+2\langle S\rangle^{2}\big(D_{34}^{y}-D_{12}^{y}\big)\theta_{c}\Delta\theta.\end{align*} \quad (3) \]
Equation (3) can be minimized by a change in the DM interactions. Such changes can occur naturally by displacing the \( PO_{4} \) tetrahedra between the Fe ions, thereby changing the exchange paths and lowering the symmetry of the crystal lattice. If such a displacement along x allows changes in the DM interactions that minimize Eq. (3), the field-induced canted structure can induce a ME response. By applying a field along b, the Zeeman term removes the Pnma symmetry elements transforming \( S_{y} \rightarrow -S_{y} \) from the spin Hamiltonian. A polarization \( P_{x} \) removes the symmetry elements that transform \( x \rightarrow -x \) . In Ref. [13] it was shown that removing these exact symmetry elements from the Hamiltonian lifts the requirement \( D_{12}^{y} = D_{34}^{y} \) , while any DM components \( D_{ij}^{x} \) or \( D_{ij}^{z} \)

FIG. 7. Magnetic structure in fields along a. The induced ferromagnetic component along a creates a spin canting in the ab plane.
are still forbidden. From Eq. (3) it can be seen that via a change of the DM components \( D_{12}^{y} \rightarrow D_{12}^{y} + \delta \) and \( D_{34}^{y} \rightarrow D_{12}^{y} - \delta \) , the DM energy is lowered by \( -\delta \langle S \rangle^{2} \partial_{c} \Delta \theta \) . Assuming that the change in DM coupling is linear in displacement, \( \delta = \lambda_{DM}^{x} x \) , the energy difference is \( \Delta E_{DM}^{p} = -4 \langle S \rangle^{2} \lambda_{DM}^{x} \partial_{c} \Delta \theta x \) . Such a displacement is resisted by the elastic forces in the lattice. The total-energy difference of the displacement is then \( -4 \langle S \rangle^{2} \lambda_{DM}^{x} \partial c \Delta \theta x + k x^{2} \) , where k is the elastic constant for \( PO_{4} \) tetrahedron displacement. This expression has a minimum at \( x = 2 k^{-1} \langle S \rangle^{2} \lambda_{DM}^{x} \partial_{c}\Delta \theta \) . Assuming the same value of the ordered moment for all four spins, \( \Delta \theta \propto \chi_{b} H_{y} \) , and assuming the polarization is proportional to the displacement x, this change in the DM terms gives a linear ME response \( P_{x} \propto 2 k^{-1} \langle S \rangle^{2} \lambda_{DM}^{z} \partial_{c} \chi_{b} H_{y} \) . This results in a ME coefficient \( \alpha_{xy}^{DM} \propto 2 k^{-1} \langle S \rangle^{2} \Lambda_{DM}^{z} \chi_{b} \) , similar to those described for other compounds in Refs. [10,47,48].
2. Field applied along a
For fields applied along \(a\), a ME effect can be mediated by the DM interaction independent of the canting component \(A_{z}\). The applied field induces a ferromagnetic component along \(x\), canting spin pairs (1, 3) and (2, 4) or (1, 4) and (2, 3), as shown in Fig. 7. The Zeeman term removes symmetry elements transforming \(S_{x} \rightarrow -S_{x}\), while an electrical polarization along \(y\) removes the symmetry elements transforming \(y \rightarrow -y\). This allows a DM term of the form \(D_{ij}^{z}\) [13]:
\[ \mathcal{H}_{\mathrm{D M}}=D_{13}^{z}\big(S_{1}^{y}S_{3}^{x}-S_{1}^{y}S_{3}^{y}\big)+D_{24}^{z}\big(S_{2}^{y}S_{4}^{x}-S_{2}^{y}S_{4}^{y}\big). \quad (4) \]
Thus, in the small-angle approximation, the change in DM energy is
\[ \Delta E_{DM}^{pol|y}=\langle S\rangle^{2}\big(\delta D_{13}^{z}+\delta D_{24}^{z}\big)\Delta\theta, \quad (5) \]
where \( \delta D_{13}^{z} \) and \( \delta D_{24}^{z} \) are changes in the DM terms upon polarization. A similar argument holds for DM terms of the form \( D_{14}^{z} \) and \( D_{23}^{z} \) . If displacing the \( PO_{4} \) tetrahedra along y would cause such nonzero DM terms \( \delta D_{13}^{z} = \delta D_{24}^{z} = \lambda_{DM}^{y} y \) , the change in DM energy of such a displacement is \( -2 \langle S \rangle^{2} \lambda_{DM}^{y} \Delta \theta \) . Using similar arguments to those for fields along b, the ME response would be \( x = k^{-1} \langle S \rangle^{2} \lambda_{DM}^{y} \chi_{a} H_{x} \) and \( \alpha_{yx}^{DM} \propto k^{-1} \langle S \rangle^{2} \lambda_{DM}^{y} X_{a} \) .

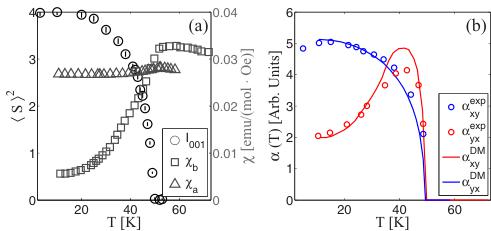
FIG. 8. (Color online) (a) The scaled intensity of the 001 peak measured on RITA-II and the molar susceptibilities for fields along a and b from Ref. [49]. (b) The measured ME coefficients \( \alpha_{xy} \) and \( \alpha_{yx} \) taken from Ref. [5] compared to the calculated temperature dependencies in arbitrary units.
3. Comparison with experiment
In this model, the ME coefficients are proportional to \( \langle S\rangle^{2}\chi \) for fields applied along both a and c. The temperature dependencies of \( \alpha_{xy} \) and \( \alpha_{yx} \) in \( \mathrm{LiFePO}_{4} \) were measured in Ref. [5]. A straightforward comparison of the DM-induced \( \alpha_{ij}(T) \) tensor components to experiment can be made by calculating the temperature dependencies of the ME coefficients directly from the experimental values of \( \langle S\rangle^{2}(T) \) and \( \chi(T) \) . We have used the temperature dependency of the intensity of the weak 001 magnetic peak, as measured on RITA-II, as a credible measure of \( \langle S\rangle^{2}(T) \) . The susceptibilities \( \chi(T) \) for fields along a and b are taken from Ref. [49], and we multiplied a proportionality factor \( d\Delta\theta/dM \) calculated from Figs. 6 and 7 assuming the same moment \( \langle S\rangle^{2} \) for all four ions. We use a scaling parameter \( C_{i}\propto\lambda_{DM}^{Di}/k \) for both \( \alpha_{xy} \) and \( \alpha_{yx} \) to fit the low-temperature response, and these are the

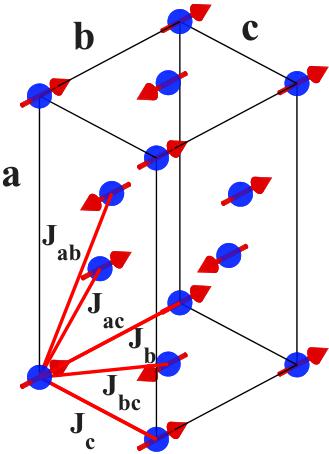
FIG. 9. (Color online) The magnetic unit cell and spin structure with the exchange couplings used in this work to analyze the spin dynamics.

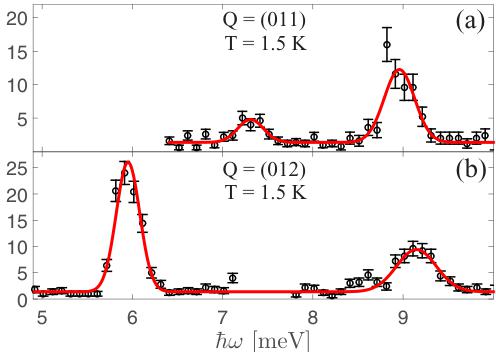
FIG. 10. (Color online) (a) and (b) Energy scans at \(Q = (011)\) and \((012)\), respectively; two distinct branches are evident in both scans. The red lines are fits to double Gaussian distributions.
only free parameters used. The scaling parameters are similar to \( C_{x}/C_{y}=0.55 \) , and the results are shown in Fig. 8.
The temperature dependencies of \( \alpha_{xy} \) and \( \alpha_{yx} \) are in good agreement with experiment at low and intermediate temperatures. The high-temperature maximum of \( \alpha_{xy} \) is slightly below the expected value. This might be due to nonidentical moment lengths at higher temperatures; a larger moment on spins 1 and 2 compared to spins 3 and 4 would reduce the asymmetry in the DM energy and hence reduce the ME response. The model gives the correct peak temperature of \( \alpha_{xy} \) , which is an improvement over the model presented in Ref. [5]. The close agreement of the \( \alpha_{yx} \) temperature dependency shows the significance of \( \langle S\rangle^{2} \) for the strength of the ME coupling, which might be of interest for future ab initio calculations.
E. Spin dynamics
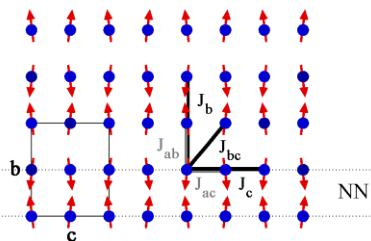
The spin excitations measured in this work have been analyzed using a similar model to that for the spin waves in \( LiNiPO_{4} \) [26,47], \( LiMnPO_{4} \) [25], and \( LiCoPO_{4} \) [14]. Three exchange parameters in the strongly coupled bc plane have been used: one nearest neighbor (NN), \( J_{bc} \) (Fe-O-Fe), two next-nearest neighbors (NNN), \( J_{b} \) and \( J_{c} \) (Fe-O-O-Fe), and two out-of-plane interactions (Fe-O-P-O-Fe), \( J_{ac} \) and \( J_{ab} \) .


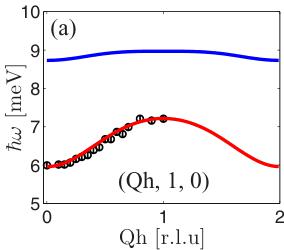
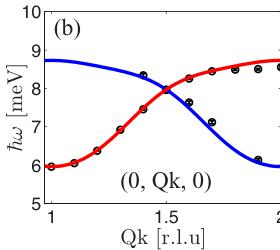
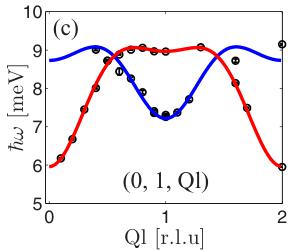
FIG. 11. (Color online) The magnetic excitations of \( LiFePO_{4} \) . (a) Measurement of the dispersion of the low-energy branch along Qh taken from Ref. [20]. (b) and (c) The data from this work, where both branches are observed. Two model dispersion branches were fitted to the data—a high-intensity one (red lines) and a low-intensity one (blue lines).
TABLE IV. The magnetic exchange interactions of LiFePO₄ in meV.
| \( J_{bc} \) | \( J_{b} \) | \( J_{c} \) | \( J_{ab} \) | \( J_{ac} \) | \( D_{a} \) | \( D_{c} \) |
| 0.77(7) | 0.30(6) | 0.14(4) | 0.14(2) | 0.05(2) | 0.62(12) | 1.56(3) |
These interactions are depicted on the magnetic unit cell in Fig. 9. We use two parameters to describe the single-ion anisotropy, \( D_{a} \) and \( D_{c} \) , allowing for an anisotropic hard plane while the anisotropy term for the easy b axis is fixed to \( D_{b}=0 \) . This is a modification of the model used in Ref. [20], where only one NNN interaction, one out-of-plane interaction, and one single-ion anisotropy parameter was used (thus, \( D_{a}=D_{c} \) , \( J_{ac}=J_{ab} \) , and \( J_{c}=J_{b} \) in terms of our model). Here we assume that the spin canting is too small to lift degeneracies in the spin-excitation spectrum, justified by the small value of the canting angle and the observation of only two excitation branches. We therefore neglect weak interactions such as the DM and anisotropic exchange interactions (as done in Ref. [10]). The following Hamiltonian is used:
\[ \mathcal{H}=\frac{1}{2}\sum_{i j}J_{i j}\mathbf{S}_{i}\cdot\mathbf{S}_{j}+\sum_{\alpha,i}D_{\alpha}S_{\alpha i}^{2}. \quad (6) \]
To calculate the spin-wave dispersion, we apply Holstein-Primakoff linear spin wave theory [26,50], assuming the ground-state magnetic structure to be purely \( C_{y} \) (see Fig. 9). The eigenenergies of the magnetic Hamiltonian are
\[ \hbar\omega=\sqrt{A^{2}-(B\pm C)^{2}}, \quad (7) \]
where
\[ \begin{aligned}A&=4S(J_{bc}+J_{ab})-2S\{J_{b}[1-\cos(\mathbf{Q}\cdot\mathbf{r}_{5})]\\&\quad+J_{c}[1-\cos(\mathbf{Q}\cdot\mathbf{r}_{6})]+J_{ac}[2-\cos(\mathbf{Q}\cdot\mathbf{r}_{7})\\&\quad-\cos(\mathbf{Q}\cdot\mathbf{r}_{8})]\}+(S-1/2)(D_{a}+D_{c}),\end{aligned} \quad (8) \]
\[ B=(S+1/2)(D_{a}-D_{c}), \quad (9) \]
\[ \begin{aligned}C&=2J_{bc}S[\cos(\mathbf{Q}\cdot\mathbf{r}_{1})+\cos(\mathbf{Q}\cdot\mathbf{r}_{2})]\\&\quad+2J_{ab}S[\cos(\mathbf{Q}\cdot\mathbf{r}_{3})+\cos(\mathbf{Q}\cdot\mathbf{r}_{4})],\end{aligned} \quad (10) \]


FIG. 12. (Color online) The structure of \( LiFePO_{4} \) projected onto the bc plane, with the in-plane couplings shown in black and the out-of-plane couplings shown in gray. The ferromagnetic ac planes are coupled to their nearest neighbors via \( J_{bc} \) and \( J_{ab} \) , in competition with the NNN couplings \( J_{b} \) and \( J_{c} \) .
and \( r_{1,2}=\frac{1}{2}(\mathbf{b}\pm\mathbf{c}) \) , \( r_{3,4}=\frac{1}{2}(\mathbf{a}\pm\mathbf{b}) \) , \( r_{5}=\mathbf{b} \) , \( r_{6}=c \) , and \( r_{7,8}=\frac{1}{2}(\mathbf{a}\pm\mathbf{c}) \) . It is evident from Eq. (9) that when \( D_{a}\neq D_{c} \) , \( \hbar\omega \) becomes multivalued and two excitation branches should be seen. This is exactly what is observed, as shown in Figs. 10(a) and 10(b), where two well-separated excitations reveal pronounced anisotropy in the hard plane.
Figure 11 shows the dispersion curves of these two observed spin-wave branches along the three principal directions (the data along Qh are taken from Ref. [20]). Using Eq. (7), we refined by nonlinear least-squares fit the exchange parameters and the single-ion anisotropies simultaneously from the branches in all three principal directions. The solid lines in Fig. 11 are calculations using Eq. (7) with the parameters that are listed in Table IV. All exchange terms are AFM in nature. From the strengths of the single-ion anisotropies compared with the exchange terms, it is clear that the system is described by a model intermediate between Ising and XY. There is a hard axis along c and an intermediate magnetic anisotropy axis a along which the anisotropy term is weaker than the exchange field but still significant. The quasi-2D nature of \( LiFePO_{4} \) is less pronounced ( \( J_{bc}/J_{ab} \approx 5 \) ) than in \( LiNiPO_{4} \) ( \( J_{bc}/J_{ab} \approx 10 \) ).
All three interactions in the strongly coupled bc plane are antiferromagnetic (AFM) leading to magnetic frustration. Evidently, \( J_{bc} \) and \( J_{ab} \) are strong enough to generate the observed commensurate structure of ferromagnetic ac planes alternating along b. Using a simple model for such layers [51], with a nearest-layer coupling of \( J_{1} \) and a next-nearest-layer coupling \( J_{2} \) , one can evaluate whether an incommensurate structure modulated perpendicular to the planes (in this case b) is energetically favorable. The criterion for spontaneous IC order is \( |J_{1}| < 4J_{2} \) . Using the effective parameters for
[1] W. Eerenstein, N. D. Mathur, and J. F. Scott, Nature (London) 442, 759 (2006).
[2] S. W. Cheong and M. Mostovoy, Nat. Mater. 6, 13 (2007).
[3] M. Kenzelmann, A. B. Harris, S. Jonas, C. Broholm, J. Schefer, S. B. Kim, C. L. Zhang, S. W. Cheong, O. P. Vajk, J. W. Lynn, Phys. Rev. Lett. 95, 087206 (2005).
LiFePO₄, namely \( J_{1}=2J_{bc}+2J_{ab}=1.76(20) \) meV and \( 4J_{2}=4J_{b}=1.14(23) \) meV, it is evident that the exchange interactions in LiFePO₄ fall short of causing spontaneous IC magnetic order. This is not the case in LiNiPO₄, where \( J_{1}=2.7(2) \) meV and \( 4J_{2}=2.68(4) \) meV [26]. This causes the Ni system to be on the verge between C and IC order, and in fact both order parameters are observed at different temperatures [10]. Contrary to LiNiPO₄, LiFePO₄ has a non-negligible \( J_{c} \) coupling, so that not only the \( J_{b} \) term but also the \( J_{c} \) and \( J_{ac} \) terms are in competition with the stronger \( J_{bc} \) and \( J_{ab} \) terms. This introduces another element of magnetic frustration within the ferromagnetic planes, as shown in Fig. 12. Whether or not there are field-induced magnetic phase transitions in LiFePO₄ as in LiNiPO₄ [52] and LiCoPO₄ [53] remains to be seen.
IV. CONCLUSION
We have determined the zero-field magnetic structure of \( LiFePO_{4} \) and found that the collinear rotation of the spins is accompanied by a spin canting of the same magnitude, and thus two distinct irreducible representations are present. These findings strongly suggest that the crystal structure may have a lower symmetry than \( P_{nma} \) at \( T_{N} \) . This deviant spin structure permits an ME effect mediated via the DM interaction for fields along b that would otherwise be impossible. The spin waves along Qk and Ql have been thoroughly measured, and two distinct branches are found, indicative of a highly anisotropic hard plane. We have determined that there are three non-negligible competing interactions in the bc plane, which introduces an element of frustration within the ferromagnetic planes that is not present in the other compounds of the family.
ACKNOWLEDGMENTS
Jens Jensen of the University of Copenhagen is greatly acknowledged for illuminating discussions. Work was supported by the Danish Agency for Science, Technology and Innovation under DANSCATT and by the Swiss NSF via Contract No. PP002-102831. Research at Ames Laboratory is supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Contract No. DE-AC02-07CH11358. Neutron experiments were performed at the Helmholtz-Zentrum Berlin für Materialien und Energie, and at the SINQ neutron spallation source at the Paul Scherrer Institute, Switzerland. We thank HZB and PSI for the allocation of neutron radiation beam time.
[4] M. Bibes and A. Barthelemy, Nat. Mater. 7, 425 (2008).
[5] M. Mercier, Ph.D. thesis, Université de Grenoble (1969).
[6] V. Aravindan et al., J. Mater. Chem. A 1, 3518 (2013).
[7] A. Yamada, S. C. Chung, and K. Hinokuma, J. Electrochem. Soc. 148, A224 (2001).
[8] M. Dubarry and B. Y. Liaw, J. Power Sources 194, 541 (2009).
[9] L. Hu et al., Nat Commun. 4, 1687 (2013).
[10] T. B. S. Jensen et al., Phys. Rev. B 79, 092412 (2009).
[11] A. Scaramucci, E. Bousquet, M. Fechner, M. Mostovoy, and N. A. Spaldin, Phys. Rev. Lett. 109, 197203 (2012).
[12] R. Toft-Petersen et al., Phys. Rev. B 85, 224415 (2012).
[13] R. Toft-Petersen, Ph.D. thesis, Tech. U. Denmark (2012).
[14] W. Tian, J. Li, J. W. Lynn, J. L. Zarestky, and D. Vaknin, Phys. Rev. B 78, 184429 (2008).
[15] A. Abragam and M. H. L. Pryce, Proc. R. Soc. London, Ser. A 206, 173 (1951).
[16] J.-P. Rivera, Ferroelectrics 161, 147 (1994).
[17] I. Kornev, M. Bichurin, J.-P. Rivera, S. Gentil, H. Schmid, A. G. M. Jansen, and P. Wyder, Phys. Rev. B 62, 12247 (2000).
[18] R. P. Santoro and R. E. Newnham, Acta Crystallogr. 22, 344 (1967).
[19] R. P. Santoro et al., J. Phys. Chem. Solids 27, 1192 (1966).
[20] J. Li, V. O. Garlea, J. L. Zarestky, and D. Vaknin Phys. Rev. B 73, 024410 (2006).
[21] D. Vaknin, J. L. Zarestky, L. L. Miller, J.-P. Rivera, and H. Schmid, Phys. Rev. B 65, 224414 (2002).
[22] C. Ederer, and N. A. Spaldin, Phys. Rev. B 76, 214404 (2007).
[23] B. van Aken, Nature (London) 449, 702 (2007).
[24] A. S. Zimmermann et al., Eur. Phys. J. B 71, 355 (2009).
[25] J. Li, W. Tian, Y. Chen, J. L. Zarestky, J. W. Lynn, and D. Vaknin, Phys. Rev. B 79, 144410 (2009).
[26] T. B. S. Jensen et al., Phys. Rev. B 79,092413 (2009).
[27] R. Toft-Petersen et al., Phys. Rev. B 84, 054408 (2011).
[28] D. Vaknin, J. L. Zarestky, J.-P. Rivera, and H. Schmid, Phys. Rev. Lett. 92, 207201 (2004).
[29] G. Liang, K. Park, J. Li, R. E. Benson, D. Vaknin, J. T. Markert, and M. C. Croft, Phys. Rev. B 77, 064414 (2008).
[30] D. Dai et al., Inorg. Chem. 44, 2407 (2005).
[31] V. I. Fomin et al., Low Temp. Phys. 28, 203 (2002).
[32] J. Rodr guez-Carvajal, FullProf: A Program for Rietveld Refinement and Pattern Matching Analysis, Abstract of the Sattelite Meeting on Powder Diffraction of the XV Congress of the IUCr (Toulouse, 1990), p. 127.
[33] J. Rodriguez-Carvajal, Physica B 192, 55 (1993).
[34] V. F. Sears, in International Tables for Crystallography, edited by A. J. C. Wilson (Kluwer, Dordrecht, 1992), Vol. C, p. 383.
[35] P. J. Brown, in International Tables for Crystallography, edited by A. J. C. Wilson (Cluwer, Dordrecht, 1992), Vol. C, p. 391.
[36] M. D. Le et al., Nucl. Instrum. Methods A 729, 220 (2013).
[37] S. Geller and J. L. Easson, Acta Crystallogr. 18, 258 (1960).
[38] P. S. Herle, B. Ellis, N. Coombs, and A. F. Nazar, Nat. Mater. 3, 147 (2004).
[39] J. Rossat-Mignod, in Methods in Experimental Physics, edited by K. Sköld and D. L. Price (Academic Press, London, 1987), Vol. 23, pt. C, p. 69.
[40] G. Rousse et al., Chem. Mater. 15, 4082 (2003).
[41] E. F. Bertaut, Acta Crystallogr. A 24, 217 (1968); see also J. Phys. (Paris) Colloq. 32, C1-462 (1971); J. Magn. Magn. Mater. 24, 267 (1981).
[42] A. S. Andersson et al., Solid State Ion. 130, 41 (2000).
[43] Z. Chen et al., J. Mater. Chem. 21, 5604 (2011).
[44] M. Reehuis, C. Ulrich, P. Pattison, B. Ouladdiaf, M. C. Rheinstädter, M. Ohl, L. P. Regnault, M. Miyasaka, Y. Tokura, and B. Keimer, Phys. Rev. B 73, 094440 (2006).
[45] T. Moriya, Phys. Rev. 120, 91 (1960).
[46] J. G. Creer and G. J. Troup, Phys. Lett. A 32, 439 (1970).
[47] T. B. S. Jensen, Ph.D. thesis, Tech. U. Denmark (2008).
[48] G. T. Rado et al., Phys. Rev. Lett. 6, 609 (1961).
[49] D. P. Chen et al., J. Appl. Phys. 101, 09N512 (2007).
[50] P. A. Lindgaard et al., Chem. Solids 28, 1357 (1967).
[51] T. Nagamiya, in Solid State Physics, edited by F. Seitz and D. Turnbull (Academic, New York, 1967). Vol. 29, p. 346.
[52] V. M. Khrustalyov et al., Czech. J. Phys. 54, 27 (2004)
[53] N. F. Kharchenko et al., Low Temp. Phys. 36, 558 (2010)