| Transition Temperature | 90 K |
|---|---|
| Experiment Temperature | 3 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | Fd-3m (#227) |
| Magnetic Space Group | I41'/am'd (#141.554) |
| Magnetic Point Group | 4'/mm'm (15.4.56) |
| Lattice Parameters | 10.10630 10.10630 10.10630 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1016/s0022-4596(03)00384-0 |
| Reference | N. Taira, M. Wakeshima, Y. Hinatsu, A. Tobo and K. Ohoyama, Journal of Solid State Chemistry (2003) 176 165-169. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Er1 | Er | 4.5 | 0.0 | 0.0 | 4.50 |
| Ru1 | Ru | -2. | 0.0 | 0.0 | 2.00 |
Magnetic structure of pyrochlore-type \( Er_{2}Ru_{2}O_{7} \)
Nobuyuki Taira, \( ^{a} \) Makoto Wakeshima, \( ^{a} \) Yukio Hinatsu, \( ^{a,*} \) Aya Tobo, \( ^{b} \) and Kenji Ohoyama \( ^{b} \)
\( ^{a} \) Division of Chemistry, Graduate School of Science, Hokkaido University, Sapporo 060-0810, Japan
\( ^{b} \) Institute for Materials Research, Tohoku University, Sendai 980-8577, Japan
Received 21 April 2003; received in revised form 30 June 2003; accepted 10 July 2003
Abstract
Powder neutron diffraction measurements were carried out for the ruthenium pyrochlore oxide \( Er_{2}Ru_{2}O_{7} \) . The magnetic structure for this compound at 3.0 K has been solved using Rietveld analysis. The observed magnetic reflections suggest that the magnetic transitions are regarded as those to a long-range ordered state. It seems that the magnetic order of the \( Ru^{4+} \) and \( Er^{3+} \) magnetic moments occurs at 90 and 10 K, respectively.
© 2003 Elsevier Inc. All rights reserved.
Keywords: Neutron diffraction; Magnetic structure; Pyrochlore; Ruthenium; Erbium
1. Introduction
Recently, oxides with the pyrochlore-type structure have attracted great attention because their unique structure of corner-sharing tetrahedra can lead to geometrical frustration and interesting physical properties at low temperatures \( [1] \) . The pyrochlore oxides, space group \( Fd\bar{3}m \) (No. 227), have eight formula units of the general formula \( A_{2}B_{2}O_{7} \) in the cubic unit cell \( [2] \) . The A and B atoms individually form a three-dimensional network of corner-sharing tetrahedra and O atoms are located around these atoms. The oxidation states for the \( A_{2}B_{2}O_{7} \) formulation are generally \( A_{2}^{2+}B_{2}^{5+}O_{7}^{2-} \) or \( A_{2}^{3+}B_{2}^{4+}O_{7}^{2-} \) . We are interested in the pyrochlore-type compounds containing rare earths (R). In those pyrochlores, the trivalent rare earth ions are situated at the A sites of the \( A_{2}B_{2}O_{7} \) , i.e., \( R_{2}^{3+}B_{2}^{4+}O_{7}^{2-}\cdot \) When both the A and B sites are occupied by magnetic ions, these compounds show very interesting magnetic features, caused by the coupled magnetic interactions between the 4f electrons of rare earths, those between the d electrons of transition metals, and those between the d and f electrons.
The structure and magnetic properties of molybdenum pyrochlore oxide \( Y_{2}Mo_{2}O_{7} \) has been studied extensively. It shows spin-glass behavior below 22 K. The highly frustrated \( Mo^{4+} \) substructure is considered to cause this behavior [3]. That is, the origin of the glassy phase is the so-called geometrical frustration inherent in the magnetic moments at the corners of the tetrahedral network. Similar behavior has also been observed for \( Tb_{2}Mo_{2}O_{7} \) [4]. The titanium pyrochlore oxides \( R_{2}Ti_{2}O_{7} \) have attracted even more attention recently. The R = Ho and Dy compounds have been discussed in terms of the “spin-ice” model [5,6]. Because the ground state is highly degenerated due to strong frustration, a static disorder state is expected down to 0 K without indication of any long-range magnetic order.
Previously, we reported the results of magnetic susceptibility and magnetic hysteresis measurements on rare earth ruthenate pyrochlores \( Y_{2}Ru_{2}O_{7} \) and \( Lu_{2}Ru_{2}O_{7} \) [7]. Both the compounds show a magnetic transition at ca. 80 K. Below this temperature, they transform to a spin-glass-like state. In these compounds, the magnetic properties can be attributed to the properties of the \( Ru^{4+} \) ions in the pyrochlore structure, because both the \( Y^{3+} \) and the \( Lu^{3+} \) ion are diamagnetic. In the following, we paid attention to the ruthenium pyrochlores \( R_{2}Ru_{2}O_{7} \) in which not only the ruthenium ion but also rare earth ions ( \( R^{3+} \) ions) are magnetic, and measured magnetic properties for \( R_{2}Ru_{2}O_{7} \) where R=Pr, Nd, and Sm-Yb [8,9]. For all of the rare earth ruthenate pyrochlores \( R_{2}Ru_{2}O_{7} \) , a
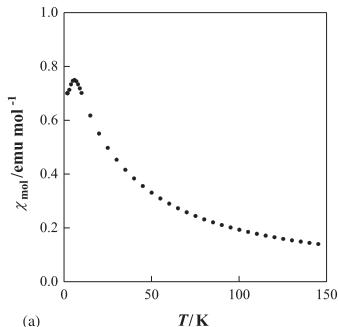
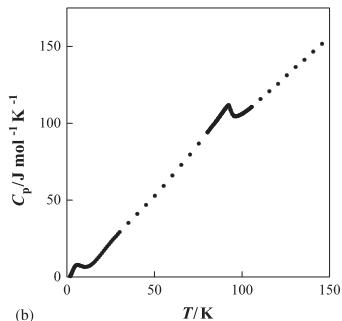
significant \( \lambda \) -type anomaly of the specific heat was observed, suggesting that the transition is the second order. Recent neutron diffraction measurements indicate that almost antiferromagnetically long-range ordered state could be realized for \( R_{2}Ru_{2}O_{7} \) below their transition temperatures, even though the low temperature phase is a spin-glass-like state in the macroscopic sense [10]. The heavy rare earth ruthenate pyrochlores \( R_{2}Ru_{2}O_{7} \) (R= Tb, Er, and Yb) show magnetic transitions at 3.4, 5.4, and 6.3 K, respectively, in the magnetic susceptibility vs. temperature curves [9]. Fig. 1 shows the temperature dependence of the magnetic susceptibilities and specific heat for \( Er_{2}Ru_{2}O_{7} \) . A \( \lambda \) -type anomaly was observed in the specific heat vs. temperature curve at ca. 95 K, indicating the existence of the long-range magnetic ordering associated with the \( Ru^{4+} \) ions below this temperature. At very low temperatures (<10 K), the presence of a magnetic interaction between the \( Er^{3+} \) ions is indicated from both the susceptibility and the specific heat data.
In order to better understand the low-temperature magnetic ordering in \( Er_{2}Ru_{2}O_{7} \) , a powder neutron diffraction study of this compound was commenced, aiming to solve its magnetic structure.


Fig. 1. (a) Temperature dependence of the magnetic susceptibilities for \( Er_{2}Ru_{2}O_{7} \) . (b) Temperature dependence of the specific heat for \( Er_{2}Ru_{2}O_{7} \) .
2. Experimental
2.1. Sample preparation
A polycrystalline sample was prepared by the conventional solid-state reaction. As starting materials, erbium sesquioxide \( Er_{2}O_{3} \) and ruthenium dioxide \( RuO_{2} \) (all with purity \( >99.9\% \) ) were used. Before use, the erbium sesquioxide was heated in air at 1270 K to remove any moisture and was oxidized to the stoichiometric composition. The starting materials were weighed in the correct metal ratio, intimately mixed in an agate mortar, and heated in air at 1320 K for 12 h. After cooling to room temperature, the sample was crushed into powders, reground, pressed into pellets, and then reheated in air at 1470 K for 36 h with several intermediate regrindings. Powder X-ray diffraction measurements were performed at room temperature with \( CuK_{\alpha} \) radiation (40 kV, 20 mA) on a Rigaku MultiFlex diffractometer equipped with a curved graphite monochromator. The results of the powder X-ray diffraction measurements on the desired pyrochlore-type compound \( Er_{2}Ru_{2}O_{7} \) revealed the presence of a very small amount of \( Er_{2}O_{3} \) . This is presumably a consequence of the loss of the more volatile ruthenium oxide.
2.2. Neutron diffraction measurements
Powder neutron diffraction patterns were collected at several temperature points from room temperature to 3 K in the angle range \( 3^{\circ} \leqslant 2\theta \leqslant 153^{\circ} \) at intervals of \( 0.1^{\circ} \) with a wavelength of 1.8196 Å. Measurements were performed on the Kinken powder diffractometer for high efficiency and high resolution measurements, HERMES, of the Institute for Materials Research (IMR), Tohoku University [11], installed at the JRR-3M Reactor in the Japan Atomic Energy Research Institute (JAERI). The fine powder sample was sealed in a vanadium cylinder with helium gas, and was mounted on the cold head of a closed cycle He-gas refrigerator.
Crystal and magnetic structures were determined by the Rietveld method [12], using the FULLPROF program [13]. Since the presence of a very small amount of \( Er_{2}O_{3} \) was detected in the sample, this second phase was included in the Rietveld refinement. The initial parameters of the pyrochlore phase \( Er_{2}Ru_{2}O_{7} \) and the second phase \( Er_{2}O_{3} \) were taken from the literatures [14,15].
3. Results and discussion
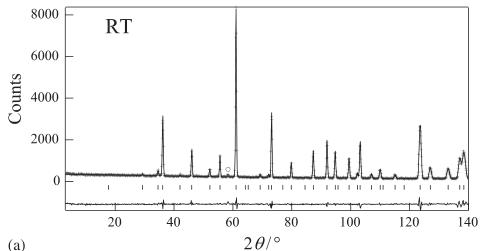
The neutron diffraction profiles for \( Er_{2}Ru_{2}O_{7} \) are shown in Fig. 2. They were analyzed by the Rietveld method. The results at room temperature agree well with


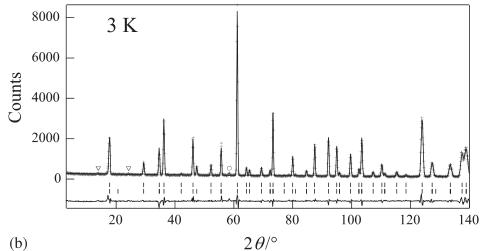
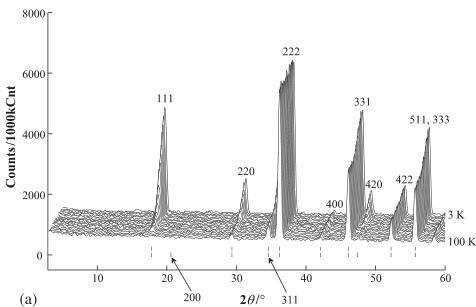
Fig. 2. (a) Powder neutron diffraction profiles for \( Er_{2}Ru_{2}O_{7} \) at room temperature. The calculated and observed profiles are shown on the solid line and cross markers, respectively. The nuclear reflection positions for \( Er_{2}Ru_{2}O_{7} \) are shown as upper vertical marks. A circle indicates the impurity phase of \( Er_{2}O_{3} \) . The lower trace is a plot of the difference between the calculated and observed intensities. (b) Powder neutron diffraction profiles for \( Er_{2}Ru_{2}O_{7}\cdot \) at 3 K. The nuclear reflection positions for \( Er_{2}Ru_{2}O_{7}\cdot \) are shown as upper vertical marks and the magnetic reflection positions are shown as lower vertical marks. Reflections marked with triangles show the magnetic reflections of the impurity \( Er_{2}O_{3} \) .
those determined by the X-ray diffraction measurements. No evidence for the oxygen-nonstoichiometry was observed; there was no measurable amount of oxygen vacancies. The Rietveld analysis also indicates that there is no intermixing between the \( Er^{3+} \) and the \( Ru^{4+} \) ions. The individual bond lengths and angles for \( Er_{2}Ru_{2}O_{7} \) are listed in Table 1. This structural feature belongs to the reported trends of the rare earth ruthenate pyrochlores [14]. Since the ratio of the impurity of \( Er_{2}O_{3} \) is below 2%, its influence on the magnetic properties of \( Er_{2}Ru_{2}O_{7} \) is considered to be negligible.
Fig. 3(a) shows the neutron diffraction profiles for \( Er_{2}Ru_{2}O_{7} \) , in the range of \( 3-60^{\circ} \) in \( 2\theta \) at various temperatures. Above 95 K, the Rietveld analyses with the space group \( Fd\bar{3}m \) have been satisfactory as well as those for the room temperature data. However, for the data below 95 K, the intensities of some Bragg reflections, especially the 111 and 220 reflections, were found to be too large to be fitted well, and some additional Bragg reflections were observed. It is considered that the excess intensities found in the Bragg
Table 1
Structural features for \( Er_{2}Ru_{2}O_{7} \) at room temp erature
| a ( \( \textup{\AA} \) ) | 10.1063(4) |
| O (1) \( \times \) | 0.3358(2) |
| \( B_{\text{iso}} \) ( \( \textup{\AA}^{2} \) ):Er | 0.31(5) |
| \( B_{\text{iso}} \) ( \( \textup{Å}^{2} \) ):Ru | 0.26(6) |
| \( B_{\text{iso}} \) ( \( \textup{A}^{2} \) ):O (1) | 0.49(4) |
| \( B_{\text{iso}} \) ( \( \textup{{Å}}^{2} \) ):O (2) | 0.13(13) |
| Ru-O(1) ( \( \textup{\AA} \) ) | 1.986(1) |
| Er-O(1) ( \( \textup{\AA} \) ) | 2.439(1) |
| Er-O(2) ( \( \textup{\AA} \) ) | 2.188(0) |
| Ru-O-Ru (deg) | 128.24(9) |
The space group is \( Fd\bar{3}m \) . Er, Ru, O (1) and O (2) atoms are at 16(d), 16(c), 48(f), and 8(b) sites, respectively.


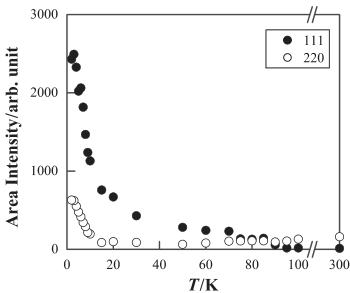
Fig. 3. (a) Neutron diffraction profiles for \( Er_{2}Ru_{2}O_{7} \) and various temperatures. (b) Temperature dependence of the integrated intensities of the 111 and 220 reflections for \( Er_{2}Ru_{2}O_{7} \) .
reflections are due to a magnetic origin. The temperature dependence of the integrated intensities of the 111 and 220 reflections is shown in Fig. 3(b). The intensities of these reflections, especially for the 111 reflection, become stronger with decreasing temperature, when the temperature is decreased through 90 K. The temperature for the onset of the increase found in the intensity vs. temperature curves ( \( \sim95 \) K) corresponds to the temperature for the \( \lambda \) -type anomaly found in the specific heat vs. temperature curve (Fig. 1b).
Furthermore, both the intensities become much stronger with decreasing temperature below ca. 10 K, which is the transition temperature associated with the magnetic ordering of \( Er^{3+} \) ions. These results are consistent with the occurrence of the magnetic orderings of the \( Ru^{4+} \) and \( Er^{3+} \) magnetic moments at 90 and 10 K, respectively. The obvious magnetic peaks have suggested that both the magnetic transitions are regarded as those to a long-range ordered state [8,9].
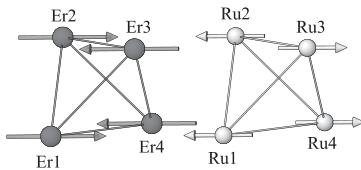
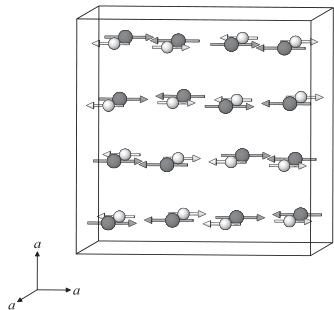
The magnetic structure for \( Er_{2}Ru_{2}O_{7} \) at 3.0 K has been determined by the analysis of the observed magnetic reflections. Fig. 2(b) shows the neutron diffraction profile of \( Er_{2}Ru_{2}O_{7} \) at 3.O K. Basically, the magnetic and the nuclear cells are identical and the magnetic moments in the face-centered metal substructure are aligned in the same direction. Among the numerous possibilities of the magnetic structure, the most reliable result has been obtained with the antiparallel arrangements of the magnetic moments as shown in Fig. 4. The atomic coordinates and the directions of the magnetic moments for \( Er^{3+} \) and \( Ru^{4+} \) ions are listed in Table 2. Fig. 4(a) shows the alignment of the magnetic moments of the \( Er_{4} \) tetrahedron and that of the \( Ru_{4} \) tetrahedron. The magnetic moments of all tetrahedra are aligned in-plane. The arrangements of the magnetic moments are consistent with the observed antiferromagnetic behavior. This compound is not a “spin-ice” one, which is represented by the Ising model, but rather, an easy-

(a)

(b)
Fig. 4. (a) Alignment of the magnetic moments in the single tetrahedra. (b) Magnetic structure of \( Er_{2}Ru_{2}O_{7} \) at \( 3.0\ K \) .
Table 2
Atomic coordinates and the direction of the magnetic moments
| Atoms | x | y | z | Direction of magnetic moments |
| Er1 | 1/2 | 1/2 | 1/2 | + |
| Er2 | 1/4 | 3/4 | 0 | − |
| Er3 | 3/4 | 0 | 1/4 | − |
| Er4 | 0 | 1/4 | 3/4 | + |
| Ru1 | 0 | 0 | 0 | − |
| Ru2 | 3/4 | 1/4 | 1/2 | + |
| Ru3 | 1/4 | 1/2 | 3/4 | + |
| Ru4 | 1/2 | 3/4 | 1/4 | − |
Note: + and - represent the direction of the magnetic moments. + is antiparallel to -.
plane (“XY model”) one, which is similar to the erbium titanate pyrochlore \( Er_{2}Ti_{2}O_{7} \) [16]. As shown in Fig. 4(b), both the magnetic moments for the \( Er^{3+} \) and \( Ru^{4+} \) ones are oriented toward the same \( \langle100\rangle \) direction, and they are anti-parallel with each other. When both kinds of magnetic ions are in an ordered state, their interaction often becomes important. The magnetic structures for some other rare-earth ruthenium pyrochlores \( R_{2}Ru_{2}O_{7} \) (R = Y and Nd) are reported [10]; they are noncollinear, complicated, and different from the present magnetic structure for \( Er_{2}Ru_{2}O_{7} \) . For the R = Y and Nd compounds, their magnetic structures consist of only the magnetic moment of the Ru ions, while for \( Er_{2}Ru_{2}O_{7} \) both the magnetic moments of the \( Er^{3+} \) and \( Ru^{4+} \) , ions are in a magnetically ordered state. The magnetic structure of rare earth ruthenate (IV) pyrochlores seems to depend on the species of the rare earth elements contained. The difference between the magnetic structures may originate from the anisotropy of the rare earth ions in the pyrochlore oxides. Since the magnetic anisotropy for the \( Er^{3+} \) ions is larger than that for the \( Ru^{4+} \) ions in this compound, the arrangement of the magnetic moments for \( Ru^{4+} \) ions may be affected by the magnetic anisotropy of \( Er^{3+} \) ions, and they are aligned in the same direction.
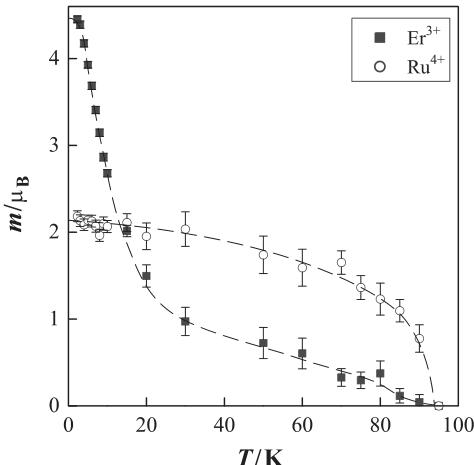
Fig. 5 shows the temperature dependence of the refined magnetic moments. The magnetic moment of the \( Ru^{4+} \) ions increases rapidly with decreasing temperature below ca. 90 K and it is saturated at \( 2.0 \mu_{B} \) , which agrees with a theoretical moment for the magnetic ion with S = 1. For the \( Er^{3+} \) ions, the magnetic moment increases with decreasing temperature and when the temperature is decreased below 10 K (the transition temperature associated with the magnetic ordering of the Er ions), the moment increases rapidly. Even at 3.0 K, however, the value for the magnetic moment of \( Er^{3+} \) ions is small ( \( 4.5 \mu_{B} \) ) compared with the theoretical value for the \( {}^{4}I_{15/2} \) ground state of \( Er^{3+} \) ion, i.e., \( 9 \mu_{B} \) . Such reduced magnetic moments have been observed in other pyrochlores containing erbium [17,18]. The magnetization M vs. the applied field H curves for

Fig. 5. Temperature dependence of the magnetic moments for the \( Er^{3+} \) and \( Ru^{4+} \) ions. Broken lines are smoothing curves for the data.
\( Er_{2}Ti_{2}O_{7} \) and \( Er_{2}Sn_{2}O_{7} \) are saturated at ca. \( 4\mu_{B} \) ( \( H\geqslant50kOe \) ). This reduction from the theoretical value for these erbium compounds may be caused by the anisotropy of the \( Er^{3+} \) ion and/or the crystal field effect.
Above 10 K, there exists a finite magnetic moment of the Er ions. The origin for this magnetic moment between 10 and 90 K is that the moment for the paramagnetic \( Er^{3+} \) ions is induced by the magnetic ordering of the \( Ru^{4+} \) ions. Moreover, the interaction between the \( Ru^{4+} \) and \( Er^{3+} \) ions may explain the long-range magnetic ordering of \( Er^{3+} \) ions at relatively higher temperature. Generally, pyrochlores containing rare earths, which have non-magnetic ions at the B-site, show magnetic transitions in the milli-Kelvin range [2]. The magnetic transition temperature, ca. 10 K, associated with the magnetic ordering of \( Er^{3+} \) ions for \( Er_{2}Ru_{2}O_{7} \) is fairly higher than those for the other pyrochlore oxides. In summary, the powder neutron diffraction measurements were carried out for the ruthenium pyrochlore oxide \( Er_{2}Ru_{2}O_{7} \) . The magnetic structure for this compound at 3.0 K has been solved by the Rietveld analysis.
Acknowledgments
The authors are indebted to the Iketani Science and Technology Foundation for the financial support.
References
[1] J.E. Greedan, J. Mater. Chem. 11 (2001) 37.
[2] M.A. Subramanian, G. Aravamudan, G.V. Subba Rao, Prog. Solid State Chem. 15 (1983) 55.
[3] J.N. Reimers, J.E. Greedan, J. Solid State Chem. 72 (1988) 390.
[4] J.N. Reimers, J.E. Greedan, S.L. Penny, C.V. Stager, J. Appl. Phys. 67 (1990) 5967.
[5] M.J. Harris, S.T. Bramwell, D.F. McMorrow, T. Zeiske, K.W. Godfrey, Phys. Rev. Lett. 79 (1997) 2554.
[6] A.P. Ramirez, A. Hayashi, R.J. Cava, R. Siddharthan, B.S. Shastry, Nature 399 (1999) 333.
[7] N. Taira, M. Wakeshima, Y. Hinatsu, J. Solid State Chem. 144 (1999) 216.
[8] N. Taira, M. Wakeshima, Y. Hinatsu, J Phys.: Condens. Matter 11 (1999) 6983.
[9] N. Taira, M. Wakeshima, Y. Hinatsu, J.Mater. Chem. 12 (2002) 1475.
[10] M. Ito, Y. Yasui, M. Kanada, H. Harashina, S. Yoshii, K. Murata, M. Sato, H. Okumura, K. Kakurai, J. Phys. Soc. Jpn. 69 (2000) 888.
[11] K. Ohoyama, T. Kanouchi, K. Nemoto, M. Ohashi, T. Kajitani, Y. Yamaguchi, Jpn. J. Appl. Phys. 37 (1998) 3319.
[12] H.M. Rietveld, J. Appl. Crystallogr. 2 (1969) 65.
[13] J. Rodríguez-Carvajal, Physica B 192 (1993) 55.
[14] B.J. Kennedy, T. Vogt, J. Solid State Chem. 126 (1996) 261.
[15] R.S. Roth, S.J. Schneider, J. Res. NBS 64A (1960) 309.
[16] R. Siddharthan, B.S. Shastry, A.P. Ramirez, A. Hayashi, R.J. Cava, S. Rosenkranz, Phys. Rev. Lett. 83 (1999) 1854.
[17] S.T. Bramwell, M.N. Field, M.J. Harris, I.P. Parkin, J. Phys.: Condens. Matter 12 (2000) 483.
[18] K. Matsuhira, Y. Hinatsu, K. Tenya, H. Amitsuka, T. Sakakibara, J. Phys. Soc. Jpn. 71 (2002) 1576.