| Transition Temperature | 11.6 K |
|---|---|
| Experiment Temperature | 1.4 K |
| Propagation Vector | k1 (0, 0, 0) |
| Parent Space Group | C2/c (#15) |
| Magnetic Space Group | P-1' (#2.6) |
| Magnetic Point Group | -1' (2.3.5) |
| Lattice Parameters | 10.26670 9.14520 5.45990 90.00 104.07 90.00 |
|---|---|
| DOI | 10.1016/j.jssc.2008.08.014 |
| Reference | G.J. Redhammer, G. Roth, W. Treutmann, W. Paulus, G. Andre, C. Pietzonka and G. Amthauer, Journal of Solid State Chemistry (2008) 181 3163-3176. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Mn1 | Mn | 4.24 | 0.78 | 1.11 | 4.19 |
Magnetic ordering and spin structure in Ca-bearing clinopyroxenes \( CaM^{2+}(Si, Ge)_{2}O_{6} \) , M = Fe, Ni, Co, Mn
Günther J. Redhammer \( ^{a,*} \) , Georg Roth \( ^{b} \) , Werner Treutmann \( ^{c} \) , Werner Paulus \( ^{d} \) , Gilles André \( ^{e} \) , Clemens Pietzonka \( ^{f} \) , Georg Amtbauer \( ^{a} \)
\( ^{a} \) Department of Materials Engineering & Physics, Division of Mineralogy, University of Salzburg, Hellbrunnerstr. 34, A-5020 Salzburg, Austria
\( ^{b} \) Institute of Crystallography, RWTH Aachen, Jägerstr. 17/19, D-52056 Aachen, Germany
\( ^{c} \) Institute of Mineralogy, Philips-University Marburg, Hans Meerweinstr., D-35032 Marburg/Lahn, Germany
\( ^{d} \) LCSIM-UMR6511, Camp. Beaulieu10B, Université de Rennes 1, Avenue de Général Leclerc, F-35042 Rennes, France
\( ^{e} \) Laboratoire Leon Brillouin (UMR12 CEA-CNRS), CEA-Saclay, F-91191 Gif-Sur-Yvette Cedex, France
\( ^{f} \) Department of Chemistry, Philips-University Marburg, Hans Meerweinstr., D-35032 Marburg/Lawn, Germany
ARTICLE INFO
Article history: Received 25 April 2008 Received in revised form 28 July 2008 Accepted 4 August 2008 Available online 19 August 2008
Keywords: Clinopyroxene Hedenbergite Magnetic properties Spin structure Neutron diffraction SQUID magnetometry
A B S T R A C T
The compounds \( CaFeSi_{2}O_{6} \) (hedenbergite), \( CaNiGe_{2}O_{6} \) , \( CaCoGe_{2}O_{6} \) and \( CaMnGe_{2}O_{6} \) have been synthesized by hydrothermal or ceramic sintering techniques and were subsequently characterized by SQUID magnetometry and powder neutron diffraction in order to determine the magnetic properties and the spin structure at low temperature. All four compounds reveal the well-known clinopyroxene structure-type with monoclinic symmetry, space group C2/c, Z=4 at all temperatures investigated. Below 35 K hedenbergite shows a ferromagnetic (FM) coupling of spins within the infinite M1 chains of edge-sharing octahedra. This FM coupling dominates an antiferromagnetic (AFM) coupling between neighbouring chains. The magnetic moments lie within the a-c plane and form an angle of \( 43^{\circ} \) with the crystallographic a-axis. Magnetic ordering in \( CaFeSi_{2}O_{6} \) causes significant discontinuities in lattice parameters, Fe-O bond lengths and interatomic Fe-Fe distances through the magnetic phase transition, which could be detected from the Rietveld refinements of powder neutron diffraction data. \( CaCoGe_{2}O_{6} \) and \( CaNiGe_{2}O_{6} \) show magnetic ordering below 18 K, the spin structures are similar to the one in hedenbergite with an FM coupling within and an AFM coupling of spins between the M1 chains. The moments lie within the a-c plane. The paramagnetic Curie temperature, however, decreases from \( CaFeSi_{2}O_{6} \) (+40.2 K) to \( CaCoGe_{2}O_{6} \) (+20.1 K) and \( CaNiGe_{2}O_{6} \) (-13.4 K), suggesting an altered interplay between the concurring AFM and FM interaction in and between the M1 chains. \( CaMnGe_{2}O_{6} \) finally shows an AFM ordering below 11 K. Here the magnetic moments are mainly oriented along the a-axis with a small tilt out from the a-c plane.
© 2008 Elsevier Inc. All rights reserved.
1. Introduction
Clinopyroxenes are a large group of \( ABC_{2}X_{6} \) compounds with a wide variety of compositions, both occurring as natural pyroxenes and as synthetic compounds. In natural material C is normally \( Si^{4+} \) (and minor \( Fe^{3+} \) , \( Al^{3+} \) ), while \( Ge^{4+} \) is only found in synthetic compounds. If the A position is occupied by \( Ca^{2+} \) , B adopts a series of divalent cations including Mg and the transition metals Ni, Co, Fe and Mn; this group of so-called 2:2 clinopyroxenes includes the minerals johannsenite \( CaMnSi_{2}O_{6} \) , hedenbergite \( CaFeSi_{2}O_{6} \) and diopside \( CaMgSi_{2}O_{6} \) , all of them adopting monoclinic C2/c symmetry. If the A site is occupied by the monovalent cations \( Na^{+} \) or \( Li^{+} \) , B hosts trivalent cations such as \( Al^{3+} \) , \( Fe^{3+} \) , \( Cr^{3+} \) , etc., these compounds are denoted as 1:3 clinopyroxenes. While having been studied in mineralogy for decades (for a compilation see e.g. [1,2]), especially 1:3 clinopyroxenes have attracted increasing interest in condensed matter physics in recent years due to their magnetic properties. This is mainly due to a distinct low-dimensional (quasi-one-dimensional) character of the atomic arrangements within edge-sharing \( MO_{6} \) chains, bearing the magnetic ions, and the fact that in some compounds spin-gap behaviour has been found. Such compounds are \( LiTi^{3+}Si_{2}O_{6} \) and \( NaTi^{3+}Si_{2}O_{6} \) [3,4], but also \( LiV^{3+}Ge_{2}O_{6} \) [5–7] and \( CaCu^{2+}Ge_{2}O_{6} \) [8–11] were intensively studied in terms of low-dimensional magnetic behaviour at low temperatures. While some compounds have a spin-gap ground state others exhibit well-developed three-dimensional (3D) antiferromagnetic (AFM) ordering such as \( LiFe^{3+}Si_{2}O_{6} \) [12], or (Li, \( Na)V^{3+} \) (Si, \( Ge)_{2}O_{6} \) ([13,14]);
also ferromagnetic (FM) ordering is found e.g. in \( NaCr^{3+}Ge_{2}O_{6} \) [15,16]. Recent theoretical calculations of the electronic structure and the magnetic properties have shed some light on the complexity of the magnetic properties of the important rock-forming mineral group of the \( (\mathrm{Na},\mathrm{Li})\mathrm{MSi}_{2}\mathrm{O}_{6} \) clinopyroxenes [17]; however the exact spin structure of several of these compounds are still not solved or are under controversial debate. The very recent discovery of multi-ferroic behaviour in clinopyroxenes [18] will certainly increase the interest in this fascinating mineral group further.
Among the Ca-bearing 2:2 clinopyroxenes investigations focussed mainly on (natural) near end-member compositions. \( CaFe_{0.8}Mg_{0.2}Si_{2}O_{6} \) shows a collinear AFM ordering below \( T_{N}=35 \) K [19], synthetic end-member \( CaFeSi_{2}O_{6} \) below \( T_{N}\sim37 \) K [20,21]. From single-crystal magnetic susceptibility measurements an AFM inter-chain interaction was proposed which competes with a FM intra-chain interaction; the magnetic spins were found to lie within the a-c plane with inclination angles of \( 45(2)^{\circ} \) towards the a- and \( 60(2)^{\circ} \) to the c-axis [20]. No neutron diffraction data are available for pure synthetic hedenbergite so far. \( CaCoSi_{2}O_{6} \) and \( CaNiSi_{2}O_{6} \) show a similar magnetic structure with AFM ordering at \( T_{N}=9.75 \) and 20.2 K, respectively [22]. As in hedenbergite the existence of a FM interaction within the \( MO_{6} \) chains was demonstrated. From neutron powder diffraction on \( CaCoSi_{2}O_{6} \) Durand et al. [22] also determined the magnitude, \( m_{0}=3.30(15)\mu_{B} \) , and the orientation of magnetic moments, which lie within a-c with an angle of \( 41^{\circ} \) to the crystallographic a-axis. Quite similar results were obtained independently by Untersteller et al. [23]. With the exception of the distorted pyroxene \( CaCuGe_{2}O_{6} \) [8–10], the magnetic properties of Ca-bearing germanate pyroxenes have not been determined yet. The present contribution describes the spin structure in the magnetically ordered state of some Ca-germanate clinopyroxenes as derived from powder neutron diffraction and of synthetic hedenbergite for comparison. Structural variations within the Ca-germanate pyroxenes will be discussed elsewhere.
2. Experimental
2.1. Material synthesis
The sample of hedenbergite was synthesized at 973 K and 0.4 GPa pressure using standard hydrothermal techniques. The redox conditions were fixed by using the \( FeO/Fe_{2}O_{3} \) solid-state buffer. To obtain the sample amount of \( \sim12 \) g necessary for neutron diffraction, several experiments were run in parallel, each one giving \( \sim1.5 \) g of sample. The resulting products were mixed, ground and rerun. This procedure was repeated twice to ensure homogeneity of the final sample. The final product was single phase and free of traces of ferric ion as proven by \( {}^{57}Fe \) Mössbauer spectroscopy. \( {}^{57}Fe \) hyperfine parameters are identical to those given in [24].
Polycrystalline sample materials of \( CaNiGe_{2}O_{6} \) , \( CaCoSi_{2}O_{6} \) and \( CaMnGe_{2}O_{6} \) were prepared from mixtures of \( CaCO_{3} \) , \( GeO_{2} \) and either \( NiO \) , \( Co_{2}O_{3} \) or MnO, respectively, in the desired stoichiometry of the compound. A ceramic solid-state sintering route was chosen to give final sample masses of \( \sim10 \) g. Therefore starting mixtures were ground under ethanol, pressed to pellets, put into an open platinum crucible and fired under ambient pressure and oxygen fugacity at a temperature of \( 1573~K \) ( \( 1473~K \) for \( CaMnGe_{2}O_{6} \) ). After a sintering time of 5 days, the sample materials were reground, pressed and reheated. This procedure was repeated 5 times. Eventually single-phase polycrystalline powders of the above-mentioned compositions were obtained, which were yellow-green for the Ni, deep pink for the Co, and pale brown for the Mn compound. The single-phase nature of the samples was tested by powder X-ray diffraction and inspection of the samples under the optical microscope.
2.2. SQUID magnetometry
The magnetic measurements were performed at the Philips-University of Marburg/Lahn on a MPMS-2 SQUID-magnetometer (Quantum Design, San Diego, USA). Small amounts of sample material (between 30 and 40 mg) were put into KLF containers and brought into measuring position using a straw. The variation of the magnetization as a function of temperature at fixed external magnetic field and as a function of the external field at fixed temperature was studied. A correction for the diamagnetism of the sample and the sample container was applied before calculating the susceptibilities from the magnetization data.
2.3. Neutron diffraction
Neutron powder diffraction experiments were performed at the ORPHEE-reactor (Laboratoire Leon Brillouin) using the G4.1 diffractometer ( \( \lambda = 2.4249 \AA \) ) in a temperature range between 1.4 and 50 K, 2 \( \theta \) range of \( 5^{\circ} \leq 2\theta \leq 88^{\circ} \) , step width 0.1°. Samples (7–12 g) were mounted into cylindrical vanadium containers. Rietveld refinements of the powder pattern were performed with FULLPROF [25]. The pseudo-Voigt function was chosen to simulate the peak shape. Intensities within 10 times of the full-width at half-maximum (FWHM) were considered to contribute to one reflection. The angular dependence of the FWHM was refined with three parameters U, V and W using the formula of Cagliotti et al. [26]. The obtained values for U, V, W are very close to the diffractometer resolution curve of the G4.1 instrument (U = 0.821, V = -0.237, W = 0.078). Initial structural parameters were taken from the room temperature structures of the corresponding compounds of this study. Magnetic structures below \( T_{N} \) were refined assuming space group P-1 for the arrangement of the magnetic atoms, an approach widely used for simple spin structures that allows to easily test spin arrangements of variable symmetry, while true magnetic space group is of higher symmetry. Different coupling models of spins were tested: pure AFM coupling in and between the chains, pure FM coupling in and between the chains or combinations of AFM and FM coupling. During refinement all components \( M_{x} \) , \( M_{y} \) and \( M_{z} \) of the magnetic moments along the crystallographic axes were allowed to vary freely.
3. Results and discussion
3.1. Magnetic measurements
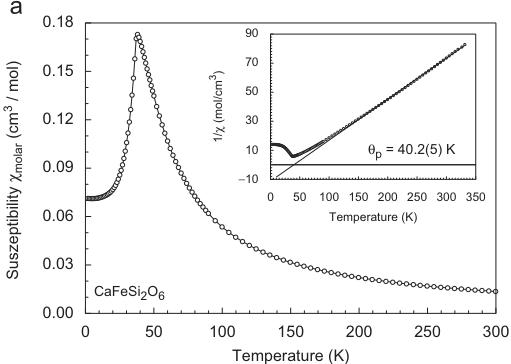
At an external field \( H_{ext} = 10 \, kG \) the magnetic susceptibility \( \chi_{molar} \) of synthetic hedenbergite \( CaFeSi_{2}O_{6} \) displays a sharp maximum at \( 38.3(2) \, K \) in its temperature dependence with the point of inflection being located at \( 35.4(2) \, K \) (Fig. 1a). The inverse magnetic susceptibility \( 1/\chi_{molar} \) (inset of Fig. 1) shows Curie–Weiss behaviour above \( \sim 100 \, K \) . Fitting a linear regression line to the data, the paramagnetic Curie temperature \( \Theta_{P} \) was found to be \( +40.2(5) \, K \) , the experimental magnetic moment \( \mu_{CW} = 5.32(8) \, \mu_{B} \) (theoretical spin-only value of \( Fe^{2+} = 4.90 \, \mu_{B} \) ). The positive paramagnetic Curie temperature suggests dominating FM coupling in hedenbergite. The ordering temperature compares well with data for hedenbergite samples in literature, which range between 36 and \( 38 \, K \) [19,20,27]. Measurements of \( \chi_{molar} \) at different external fields \( H_{ext} \) reveal a small temperature




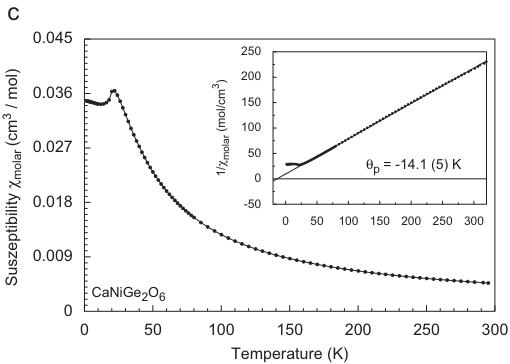
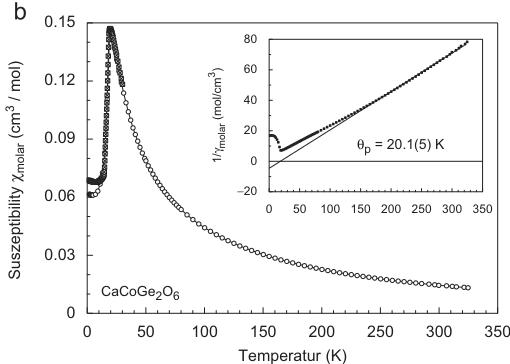
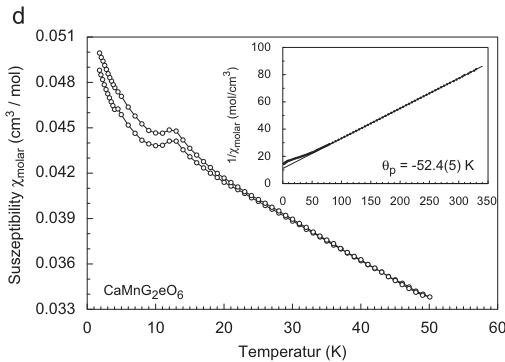
Fig. 1. Temperature dependence of the magnetic susceptibility and inverse magnetic susceptibility (inset) for (a) hedenbergite \( CaFeSi_{2}O_{6} \) , (b) \( CaCoGe_{2}O_{6} \) , (c) \( CaNiGe_{2}O_{6} \) and (d) \( CaMnGe_{2}O_{6} \) ; data in (a–c) were measured at an external magnetic field \( H_{ext} = 10 \) kG, the susceptibility for \( CaMnGe_{2}O_{6} \) was measured at 0.5 kG, the insets all show 10 kG data.
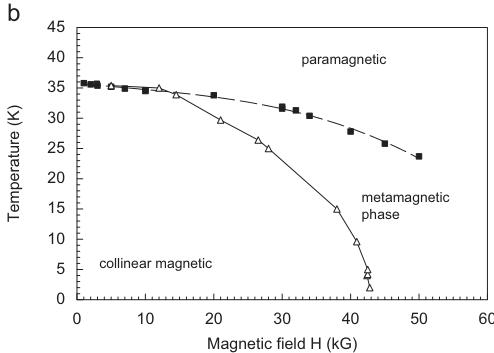
dependence of \( T_{N} \) . While at 1 kG the point of inflection is observed at 35.8 K, it is 23.7 at \( H_{ext} = 50 \) kG, the highest field we could apply (Fig. 2). The paramagnetic Curie temperature \( \Theta_{P} \) (38.9–40.5 K) and the Curie constant \( C_{m} \) however remain almost constant.
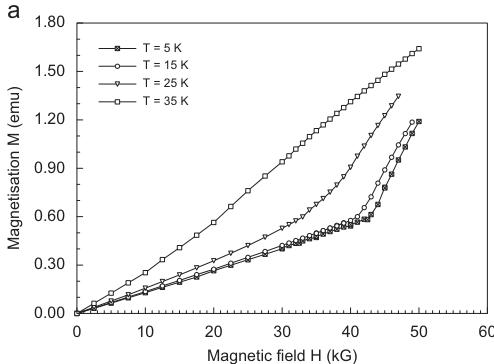
The magnetization \( M = f(H) \) at 2 K is linear up to a critical field of 42.5 kG, at higher fields a sharp kink is observed. This behaviour can be interpreted either as a spin-flop or as a meta-magnetic transition. A spin-flop transition is found e.g. in the structurally isotypic silicate \( CaCoSi_{2}O_{6} \) [23], however occurring at much lower critical fields of 12.5 kG. High field measurements on the same synthetic hedenbergite sample studied here, indicate that at \( H_{ext} \sim 120 \) kG saturation is reached, however linear regression curves fitted to the high field magnetization data do not cross the zero field/zero temperature origin [28]. Thus it is preferred to ascribe the observed kink in the field-dependent magnetization of hedenbergite to a meta-magnetic transition. The critical field of the meta-magnetic transition decreases with increasing temperature. This is evident from the \( T-H_{ext} \) phase diagram, which could be constructed from the available data. (Fig. 2b).
The germanate compounds \( CaMgE_{2}O_{6} \) ( \( M = Ni^{2+}, Co^{2+}, Mn^{2+} \) ) all show magnetic ordering at low temperature. The magnetic susceptibility \( \chi_{molar} \) of synthetic \( CaCoGe_{2}O_{6} \) (Fig. 1b) exhibits a maximum at 18.9–19.5 K, slightly depending on the external magnetic field H, the point of inflection appears to be almost independent of the external field. It is located at 18.3(1)K at \( H_{ext} = 50 \) G and at 18.1(1)K at \( H_{ext} = 10 \) kG. The Néel temperature in \( CaCoGe_{2}O_{6} \) is larger than in the analogue silicate compound with \( T_{N} = 10.0 \) K [22] and 9.3 K [23,29]. The inverse magnetic susceptibility \( 1/\chi_{molar} \) of \( CaCoGe_{2}O_{6} \) (inset in Fig. 1b) shows Curie–Weiss behaviour above \( \sim 150 \) K. Fitting a linear regression to the data above 150 K, the paramagnetic Curie temperature \( \Theta_{P} \) was found to be \( +20.1(5) \) K, the experimental magnetic moment \( \mu_{CW} = 5.21 \) \( \mu_{B} \) . This experimental moment is distinctly larger than the theoretical spin-only value \( Co^{2+} = 3.87 \) \( \mu_{B} \) [30]. However a similar large value of 5.52 \( \mu_{B} \) is reported by Durand et al. [22] for the analogue silicate \( CaCoSi_{2}O_{6} \) and Geray [29] give a value of \( 5.3 \) \( \mu_{B} \) for the silicate. The effective magnetic moments of \( Co^{2+} \) in the clinopyroxenes, determined from susceptibility measurements, are either overestimated due to a too low-temperature region for fitting a Curie–Weiss law to the data or strong spin–orbit coupling (SOC) plays an important role here as is to be expected for a \( 3d^{7} \) system. As in hedenbergite the positive paramagnetic Curie temperature suggests a dominating FM coupling of magnetic moments in \( CaCoE_{2}O_{6} \) . This is in some contrast to the silicate \( CaCoSi_{2}O_{6} \) , which shows a negative paramagnetic Curie temperature of \( \Theta_{P} = -28 \) K [22], while in [29] \( \Theta_{P} = -12.3 \) K is found. The field dependence of the magnetization at fixed temperatures is strictly linear in the accessible field range up to 55 kG. Thus the germanate shows


Fig. 2. Field dependence of the magnetization in synthetic hedenbergite CaFeSi₂O₆ at different temperatures (a) and temperature-field phase diagram for hedenbergite (b).
different behaviour to the analogue silicate which displays a spin-flop around 11.2–12.5 kG [23,29].
At 10 kG the magnetic susceptibility \( \chi_{molar} \) of synthetic \( CaNiGe_{2}O_{6} \) (Fig. 1c) shows a maximum at 20.6 K, the point of inflection is located at 18.1 K. The Néel temperature is almost identical to \( CaNiSi_{2}O_{6} \) , where the point of maximum inclination in the susceptibility is reported at 20.2 K [29] and 21.7 K [23], respectively. The inverse magnetic susceptibility shows Curie–Weiss behaviour above 80 K, the fitting of a regression line to the data in the paramagnetic range yields a negative paramagnetic Curie temperature of \( \theta_{P} = -14.1 \) K and an effective magnetic moment \( \mu_{CW} = 3.39 \mu_{B} \) , which is again higher than the spin-only value for \( Ni^{2+} \) (2.83 \( \mu_{B} \) per \( Ni^{2+} \) cation). The negative \( \theta_{P} \) for the \( Ni^{2+} \) germanate is in contrast to the positive ones for the \( Fe^{2+} \) and \( Co^{2+} \) compounds and also to the silicate analogue \( CaNiSi_{2}O_{6} \) . In the latter compound, a positive paramagnetic Curie temperature of \( +27.6 \) K [29] and \( +31 \) K [22], respectively, is reported. The effective magnetic moment in the latter two studies is 2.77 and \( 2.82 \mu_{B} \) , close to the theoretical spin-only value. Similar to \( CaCoGe_{2}O_{6} \) , the field dependence of the magnetization at fixed temperatures is strictly linear in the accessible field range up to 55 kG for \( CaNiGe_{2}O_{6} \) .
The temperature dependence of the magnetic susceptibility in \( CaMnGe_{2}O_{6} \) is somewhat different from the ones in the previous compounds as it does not reveal such a distinct maximum in the
Table 1
Magnetic data of synthetic CaM(Ge, Si) \( _{2} \) O \( _{6} \) clinopyroxene compounds from magnetization measurements
| Sample | T_{N} (K) @ 50 G | \( \mu_{\text{CW}} \) ( \( \mu_{\text{B}} \) ) | \( \theta_{\text{P}} \) (K) |
| CaFeSi_{2}O_{6} | 35.4(2) | 5.32 | 40.2(5) |
| CaCoGe_{2}O_{6} | 18.3(2) | 5.21 | 20.1(5) |
| CaNiGe_{2}O_{6} | 18.1(2) | 3.39 | -13.4(5) |
| CaMnGe_{2}O_{6} | 11.6(2) | 6.04 | -52.4(5) |
\( T_{N} \) = Neel temperature, \( \mu_{CW} \) = experimental magnetic moment, \( \theta_{P} \) = paramagnetic Curie temperature, determined from Curie–Weiss behaviour.
magnetization (Fig 1d). At higher external fields, only a very weak "bump" can be detected. At low external fields, however, a well-developed peak is observable (Fig. 1d), marking the onset of magnetic ordering. The peak susceptibility is observed at 12.4(2)K, while the point of inflection is found at 11.5(2)K. The inverse magnetic susceptibility strictly follows a Curie–Weiss behaviour above 50K and from this the paramagnetic Curie temperature is determined to be strongly negative with \( \theta_{P} = -52.4(5) \) K and the effective magnetic moment \( \mu_{CW} = 6.04 \mu_{B} \) per \( Mn^{2+} \) cation. This suggests a strong AFM ordering in \( CaMnGe_{2}O_{6} \) .
The field dependence of the magnetization at fixed temperatures is strictly linear in the accessible field range up to \( 55 \, kG \) for \( CaMnGe_{2}O_{6} \) . The magnetic data for all four samples are compiled in Table 1.
3.2. Neutron diffraction
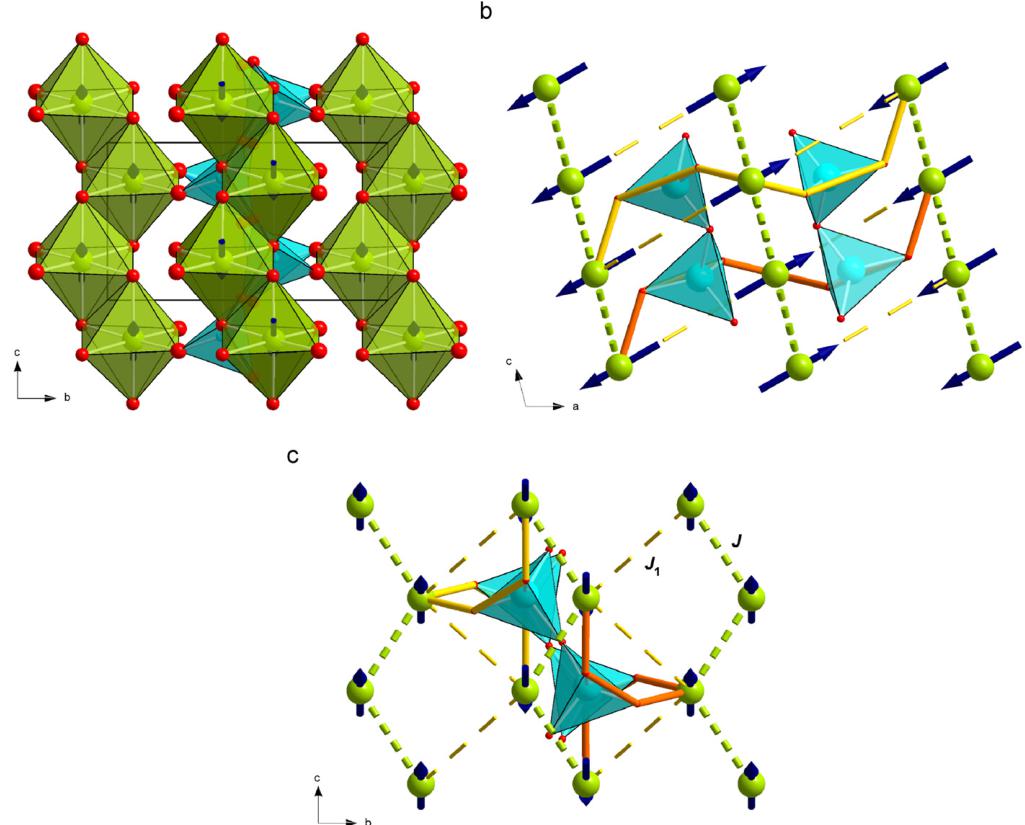
All four compounds show monoclinic symmetry and the atomic structures retain C2/c symmetry over the complete temperature range. The C2/c clinopyroxene structure is well described in several studies \( [1,4,11,31-33] \) thus only some basic outlines will be given here: the main geometric building units are infinite zig-zag chains of edge-sharing M1 octahedra parallel to the crystallographic c-direction; these octahedra host the transition metal cations. The M1 chains are linked to each other by infinite kinked chains of corner-sharing \( GeO_{4} \) or \( SiO_{4} \) tetrahedra; the interstitial space is filled by M2 \( Ca^{2+} \) cations, which are in 8-fold oxygen coordination. A polyhedral representation is given below.
3.2.1. Hedenbergite CaFeSi_{2}O_{6}
For \( CaFeSi_{2}O_{6} \) neutron diffraction patterns were recorded between 1.4 and 52 K. The refinements of the atomic structure were done starting from the atomic model of synthetic hedenbergite at 100 K, given in [24]. Experimental data and refinement results of the 1.4 K measurements are compiled in Table 2, fractional atomic coordinates are listed in Table 3 and some basic derived structural data are listed in Table 4. The components and total magnetic moments at 1.4 K are listed in Table 5. The complete set of atomic coordinates and structural parameters for hedenbergite and the germanates, at all temperatures, is available from the crystallographic information files (CIFs), which will be deposited.
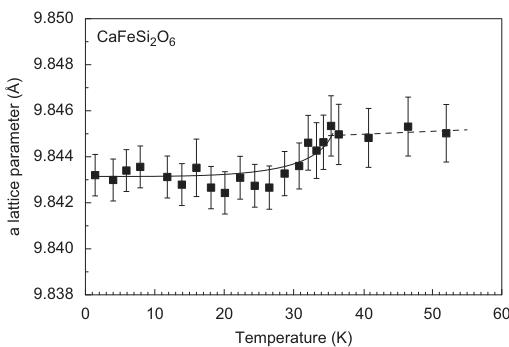
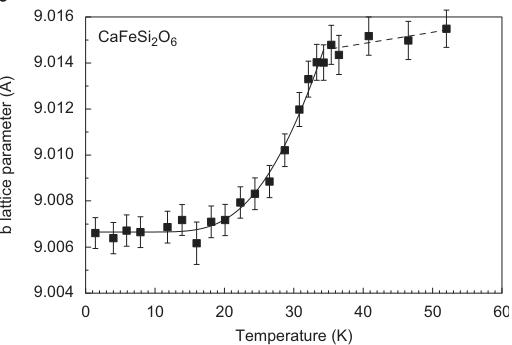
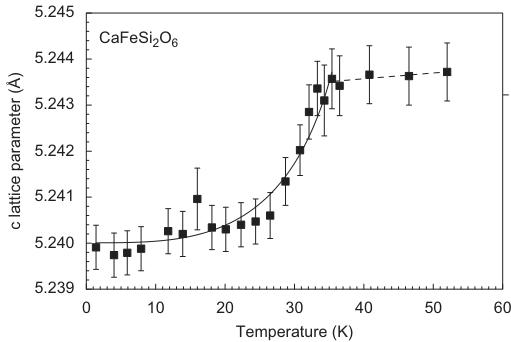
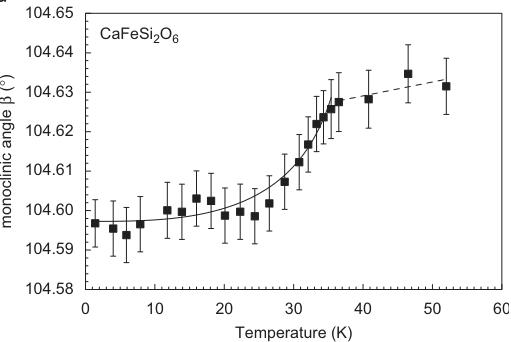
The evolution of lattice parameters as a function of temperature in hedenbergite is displayed in Fig. 3. Except for a, very prominent discontinuities are observable between 30 and 35 K. This shrinking of the lattice is related to the magnetic ordering of the sample, i.e. is the result of a distinct magnetostriction of the lattice. For neutron diffraction measurements on antiferromagnets, additional reflections appear at low temperatures below \( T_{N} \) . They can be indexed using the same unit cell as for the atomic
Table 2 Experimental details and results for Rietveld refinements at T = 1.4 K
| CaFeSi2O6 | CaNiGe2O6 | CaCoGe2O6 | CaMnGe2O6 | |
| M1 | 337.11 | 339.96 | 340.19 | 336.19 |
| Cell setting, space group | Monoclinic, C2/c | Monoclinic, C2/c | Monoclinic, C2/ | Monoclinic, C2/ |
| a (Å) | 9.8432(9) | 10.1150(7) | 10.1477(5) | 10.2667(5) |
| b (Å) | 9.0067(7) | 8.9416(5) | 8.9518(5) | 9.1452(5) |
| c (Å) | 5.2399(5) | 5.4139(3) | 5.4274(4) | 5.4599(4) |
| β (deg.) | 104.596(7) | 105.203(5) | 104.754(5) | 104.071(5) |
| V (Å3) | 449.55(7) | 472.52(5) | 476.77(5) | 497.26(5) |
| Z | 4 | 4 | 4 | 4 |
| Sample colour | Light beige | Light green | Pink | Light brown |
| 2θmin (deg.) | 10.00 | 10.00 | 10.00 | 10.00 |
| 2θmax (deg.) | 89.90 | 89.90 | 89.90 | 89.90 |
| Increment (deg.) | 0.1 | 0.1 | 0.1 | 0.1 |
| Rp (%) | 5.136 | 5.172 | 4.836 | 3.625 |
| Rwp (%) | 7.195 | 6.980 | 6.811 | 4.901 |
| Rexp (%) | 1.198 | 2.346 | 1.897 | 1.854 |
| Rb (%) | 4.093 | 4.812 | 2.914 | 1.485 |
| Rb magn (%) | 8.06 | 8.91 | 8.52 | 2.37 |
| (A/B)max | <0.0001 | <0.0001 | <0.0001 | <-0.0001 |
Constant wavelength neutron diffraction, \( \lambda = 2.4249 \) Å, G 4-1 diffractometer (LLB), step scan data, refinement on \( F^{2} \) , pseudo-Voigt function, no excluded regions.
Table 3
Fractional atomic coordinates in the four clinopyroxene compounds at 1.4 K, as extracted from Rietveld refinement on neutron diffraction data
| Site | x | y | z | B ( \( \textup{\AA}^{2} \) ) |
| CaFeSi \( _2 \) O \( _6 \) | ||||
| Fe | 0 | 0.9079(6) | \( \frac{1}{4} \) | 0.50(9) |
| Ca | 0 | 0.3021(14) | \( \frac{1}{4} \) | 0.63(8) |
| Si | 0.2874(10) | 0.0948(13) | 0.2298(21) | 0.29(9) |
| O1 | 0.1187(7) | 0.0904(8) | 0.1544(12) | 0.48(12) |
| O2 | 0.3619(8) | 0.2463(7) | 0.3201(13) | 0.71(12) |
| O3 | 0.3510(7) | 0.0201(7) | -0.0099(14) | 0.42(13) |
| CaNiGe \( _2 \) O \( _6 \) |
reflections. The most prominent additional Bragg reflections are (100), (010), (210) and (211). From the neutron diffraction data, the onset of magnetic ordering takes place between 33.3 and 34.3 K (Fig. 4a). The magnetic intensities in the 33.3 K data set however are only slightly above the background and could not be modelled well in the Rietveld refinements. The onset of the magnetic ordering in neutron diffraction experiments is found at somewhat lower temperatures which may be due to small
Table 4
Derived structural data for the clinopyroxene compounds at 1.4 K
| CaFeSi2O6 | CaNiCe2O6 | CaCoGe2O6 | CaMnGe2O6. | |
| M1-01 (Å) | 2.147(7) | 2.122(6) | 2.123(8) | 2.206(7) |
| M1-01 (Å) | 2.147(7) (2.163(7) | 2.126(7) | 2.126(7) | 2.256(7) |
| M1-02 (Å) | 2.087(6) | 2.083(7) | 2.074(8) | 2.071(7) |
| <M1-O> (Å) | 2.127 | 2.122 | 2.108 | 2.176 |
| M1-M1(intra) (Å) | 3.101(4) | 3.118(4) | 3.135(8) | 3.254(5) |
| M1-M1(inter) (Å) | 5.716(4) | 3.855(5) | 5.877(9) | 5.903(6) |
| M1-O1-M1 ( \( ^{\circ} \) ) | 92.5(2) | 93.4(2) | 95.1(2) | 93.8(2) |
| M1-O2-O1 ( \( ^{\circ} \) ) | 149.69(2) | 146.6(2) | 144.9(2) | 142.8(2) |
| O2-O1-M1 ( \( ^{\circ} \) ) | 121.81(2) | 123.7(2) | 124.4(2) | 124.8(2) |
| Ca-O1 (Å) | 2.356(8) | 2.381(9) | 2.386(9) | 2.343(8) |
| Ca-O2 (Å) | 2.360(9) | 2.404(7) | 2.383(6) | 2.366(7) |
| Ca-O3 (Å) | 2.618(8) | 2.567(9) | 2.602(9) | 2.665(8) |
| Ca-O3 (Å) | 2.689(8) | 2.624(9) | 2.675(10) | 2.749(8) |
| <Ca-O> (Å) | 2.506 | 2.494 | 2.516 | 2.531 |
| T-O1 (Å) | 1.607(7) | 1.613(8) | 1.726(8) | 1.729(7) |
| T-O2 (Å) | 1.564(7) | 1.701(8) | 1.702(8) | 1.714(7) |
| T-O3 (Å) | 1.680(7) | 1.822(8) | 1.779(7) | 1.794(7) |
| T-O3 (Å) | 1.700(7) | 1.862(7) | 1.802(8) | 1.798(7) |
| <T-O> (Å) | 1.638 | 1.750 | 1.752 | 1.758 |
| O3-O3-O3 \( ^{\circ} \) | 163.8(2) | 160.58(2) | 157.5(2) | 158.3(2) |
Table 5
Components and resulting total magnetic moments in the four clinopyroxene compounds at 1.4 K, as extracted from Rieveld refinement on neutron diffraction data
| CaFeSi2O6 | CaNiGeo2O6 | CaCoGe2O6 | CaMnGe2O6, | |
| Mx(μB) | 3.45(4) | 0.92(4) | 1.92(4) | 4.24(7) |
| My(μB) | - | - | - | 0.78(9) |
| Mz(μB) | 3.37(4) | 1.94(4) | 2.75(5) | 1.11(7) |
| M(μB) | 4.83(4) | 2.09(4) | 3.28(5) | 4.44(7) |
| 2√(S(S+1)μB) | 4.90 | 2.83 | 3.87 | 5.92 |
| ∠(a, M)(°) | 45.4 | 63.7 | 54.2 | 14.3 |
| ∠(a/c, M)(°) | - | - | - | 10.4 |
- = theoretical spin only value of the magnetic moment, \(\angle(a, M) = \text{angle}\) between the magnetic moment and the crystallographic \(a\)-axis, \(\angle(a, C, M) = \text{angle}\) between the magnetic moment and the crystallographic \(a-c\) plane.
a

b

C

d

Fig. 3. Variation of unit cell dimensions as a function of temperature in synthetic hedenbergite \( CaFeSi_{2}O_{6} \) from powder neutron diffraction data. Lines fitted to the data are guides to the eye only.
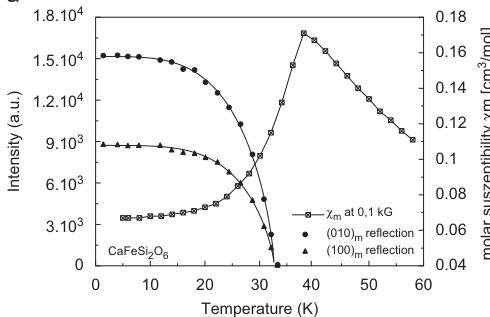
differences in the temperature calibrations between neutron diffraction and SQUID experiments. Also it is well known that first magnetic Bragg reflections in diffraction experiments generally appear at somewhat lower temperatures than the "thermodynamic" ordering temperature due to the need of coherent scattering domains. The intensity \( I_{h k}(T) \) of the two prominent magnetic reflections (100) and (010) was fitted with a phenomenological power law \( I_{h k}(T) = \mathbb{C}[1 - (T/T_{\mathrm{N}})^{\alpha}]^{\beta} \) where C is a constant, \( T_{N} \) is the magnetic transition temperature, \( \varepsilon = 2\beta \) ; \( \beta \) corresponds to the critical exponent [34]. This formula can be used to describe the intensity variation \( I_{h k}(T) \) in the whole temperature region below \( T_{N} \) . From the fits to the data (Fig. 4a) the critical exponent is \( \beta = 0.34(2) \) and 0.36(3) for the (010) and the (010) Bragg reflection, respectively, with \( T_{N} = 32.6(1) \) K.
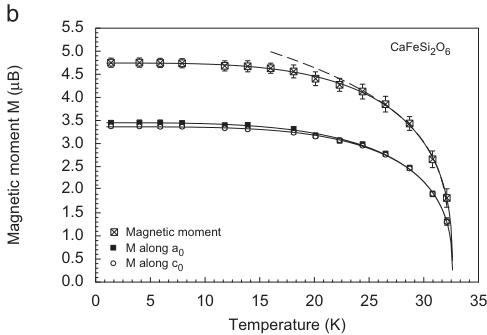
The solution of the magnetic structure was done in space group P-1 and several coupling schemes where tested arbitrarily. The only model yielding a good refinement of diffraction data has a FM coupling of magnetic moments within the M1 chain, from chain to chain however, the moments are antiparallel (AFM). The moments are aligned within the a–c plane (Fig. 4b, Table 5). There is no component of the magnetic moment along the crystallographic b-axis. This can be deduced from the presence of \( (0k0) \) reflections with \( k = 2n+1 \) [22]. The total magnetic moment in hedenbergite is \( 4.83(6)\mu_{B} \) per \( Fe^{2+} \) cation which is close to the theoretical spin-only value of \( 4.90\mu_{B} \) [30]. From this it can be concluded that in susceptibility measurements the effective magnetic moments are slightly overestimated and that no spin–orbit coupling is present for \( Fe^{2+} \) in hedenbergite. Below 20K there is no significant change in the magnitude of the magnetic moments, i.e. saturation is reached. The magnetic moments in hedenbergite form an angle of \( 43.1-44.2^{\circ} \) with the crystallographic a-axis (Fig. 5). The results of the neutron diffraction experiments on the synthetic hedenbergite powder are in good quantitative agreement with the findings of Baum et al. [20]. In a magnetic susceptibility study on a natural hedenbergite single crystal these authors determined the magnetic moments to be aligned in the a–c plane with an angle of \( 45(2)^{\circ} \) from a. The magnetic moment data of this study, derived from neutron diffraction were fitted with a phenomenological power law similar to the one given by Blundell et al. [35]: \( M(T) = M(0)[1 - (T/T_{\mathrm{N}})^{\alpha}]^{\beta} \) with \( T_{N} = 32.6(1) \) , \( \alpha = 3.65(3) \) and \( \beta = 0.34(1) \) . This power law forces a \( M(T) \propto [1 - (T/T_{\mathrm{N}})]^{\beta} \) behaviour in the critical region near \( T_{N} \) while a \( M(T) = M(0)[1 - cT^{\alpha}] \) behaviour is obtained at \( T \rightarrow 0 \) [35]. A fit in the critical region \( T_{N} - 15K \) (dashed line in Fig. 4b) yields a critical exponent \( \beta = 0.29(1) \) and \( T_{N} = 32.3(1) \) . These critical exponents are consistent with a 3D model of ordering, i.e. a 3D Heisenberg \( (\beta_{\mathrm{ideal}} = 0.366) \) or a 3D Ising model \( (\beta_{\mathrm{ideal}} = 0.366) \) , but are far from the ideal value for a 2D Ising model \( (\beta_{\mathrm{ideal}} = 0.125; [36]) \) . It is, however, not possible to discern between the two 3D models.


Fig. 4. (a) Integral intensity of the two prominent magnetic reflections (100) and (010) of \( CaFeSi_{2}O_{6} \) as a function of temperature, fitted with a power law (see text for details), in comparison to the magnetic susceptibility. (b) Total magnetic moment and its components along x and z in \( CaFeSi_{2}O_{6} \) from powder neutron diffraction as a function of temperature, fitted with a power law (error bars are only shown for the total magnetic moment for clarity).
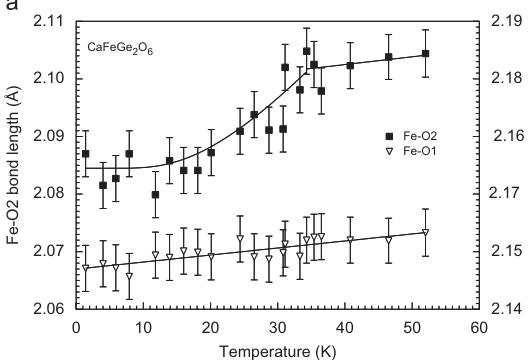
based solely on our experimental data. Theoretical calculations may shed some more light to this topic and are under progress. Generally, the Heisenberg model handles the spin as a 3D vector (dimensionality of the spin D = 3) thus allowing also spin canting, while the Ising model considers the z-component of the spin \( (D = 1) \) only and forces the spins to be strictly parallel/antiparallel pointing either "up" or "down" [36]. This dimensionality D of the spin-vector has to be distinguished from the dimensionality d of the lattice on which the spins sit and which can be 1, 2, etc. and which is d = 3 in the present case (3D ordering). The positive paramagnetic Curie temperature \( \theta_{P} \) in \( CaFeSi_{2}O_{6} \) (Table 1) shows that a strong FM coupling within the chains dominates over the weak AFM coupling between the chains. Indeed, in electronic and magnetic structure calculations found intra-chain coupling constants J of \( \sim+20~cm^{-1} \) (depending on cluster size), while the inter-chain coupling \( J_{1} \) is around \( -4~cm^{-1} \) [27], supporting the above statement. Some discussion exits concerning the inter-chain coupling. The exchange interaction \( J_{1} \) between two nearest M1 chains involves the edge of one \( SiO_{4} \) tetrahedron and is defined by the pathway Fe-O1-O1-Fe (Fig. 5), while another exchange interaction \( J_{2} \) is discussed involving two tetrahedra [18]. At 1.4 K the angles at the bridging oxygen atoms between the two chains are \( 149.7(1)^{\circ} \) and \( 121.8^{\circ} \) for the Fe-O1-O2 and O1-O2-Fe, respectively, both values consistent with an AFM coupling. As the magnetic phase transition has some distinct effects on unit cell dimensions of hedenbergite, it is of interest to look for discontinuities in structural parameters corresponding to these discontinuities. While the Fe–O1 bond lengths increase slightly and linearly between 1.4 and 52 K, the Fe–O2 bond length shows such a discontinuity across the magnetic phase transition (Fig. 6a). The O2 oxygen atom is involved in magnetic coupling between the chains. The Si–O bond lengths behave rigid and show no significant alterations with temperature, while the O3–O3–O3 bridging angle slightly increases with decreasing temperature in the magnetically ordered phase; i.e. the tetrahedral chain gets slightly more straightened with decreasing temperature. Small variations in Ca–O3 bond lengths can be related to the changes in the bridging angle of the tetrahedral chain.
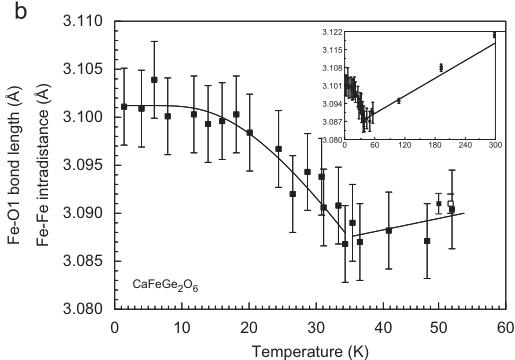
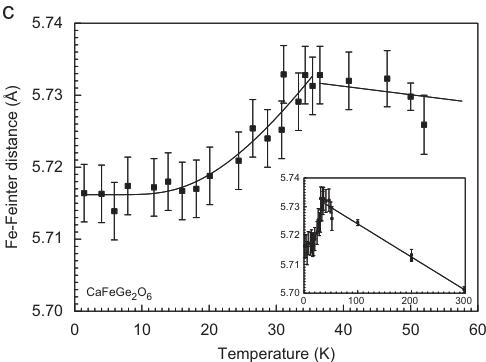
Within the M1 chain the Fe–O1–Fe interatomic angle decreases down to \( \sim35 \) K; below this temperature it increases with decreasing temperature. Fe–Fe distances within and between two neighbouring M1 chains reflect the magnetic ordering in a distinct way: the Fe–Fe \( _{\text{(inter)}} \) distance decreases with decreasing temperature from \( 3.121(1)\mathring{A} \) at 298 to \( 3.087(4)\mathring{A} \) at \( \sim35 \) K, but then increases (Fig. 6b). Data for CaFeSi \( _{2} \) O \( _{6} \) at 100, 200 K and RT from [24] are included in the inset of Fig. 6a to justify the trends from low-temperature neutron data. The opposite behaviour is observed for the Fe–Fe \( _{\text{(inter)}} \) distances (Fig. 6c). These increase upon cooling from \( 5.690(1)\mathring{A} \) [24] to \( 5.733(4)\mathring{A} \) , but then decrease again within the magnetically ordered phase. This behaviour shows that the FM coupling of spins below \( T_{N} \) in hedenbergite moves the \( Fe^{2+} \) cations within the M1 chain away from each other (resulting in an increase of the M1–O–M1 angle), while the AFM coupling between the chains moves them closer to each other.
The shortening of the Fe–Fe \( _{(\text{inter})} \) distance goes along with the shortening of the Fe–O2 bond length, which is directly involved in exchange interaction \( J_{1} \) . For comparison, there is no discontinuity in the bond lengths of the tetrahedral site, which remain almost unaltered by phase transition and temperature variation between 1.4 and 52 K. The changes in lattice parameters along b and c are mostly related to the changes in interatomic distances involving the M1 sites.
3.2.2. CaCoGe_{2}O_{6}
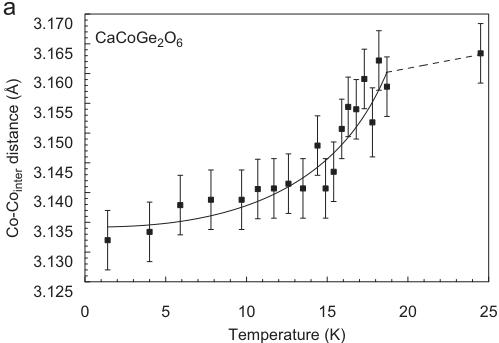
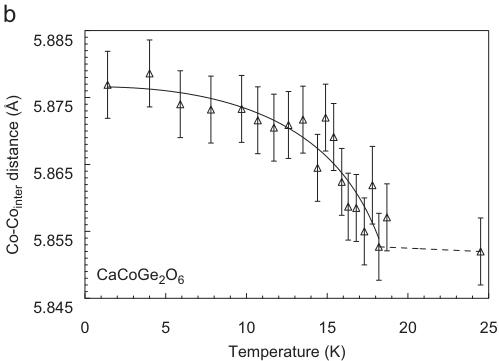
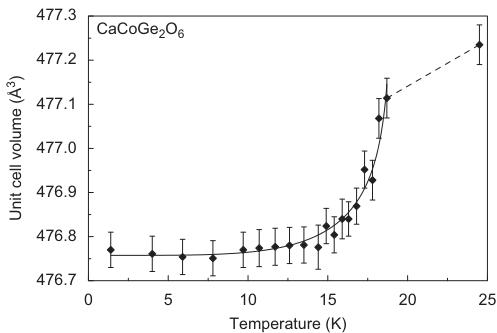
For \( CaCoGe_{2}O_{6} \) , the neutron diffraction experiments were performed in a temperature range between 1.4 and 24.0 K. The Rietveld refinements of data were done starting from the fractional atomic coordinates of the neutron diffraction experiment of hedenbergite at 1.4 K. The replacement of \( Si^{4+} \) by \( Ge^{4+} \) causes the a- and the c-lattice parameters in \( CaCoGe_{2}O_{6} \) to be distinctly larger than the ones in hedenbergite or the analogue silicate. In comparison between the Co-silicate and the Co-germanate, the a-lattice parameter increases by \( \sim0.35\mathring{A} \) , c by \( \sim0.18\mathring{A} \) , while b remains constant and the monoclinic angle decreases by \( \sim0.75^{\circ} \) . The temperature-dependent evolution of lattice parameters at low temperature is similar to the one in hedenbergite: At the magnetic phase transition small discontinuities are observed with the magnetically ordered phase showing smaller lattice parameters and consequently a smaller unit cell volume (Fig. 7).
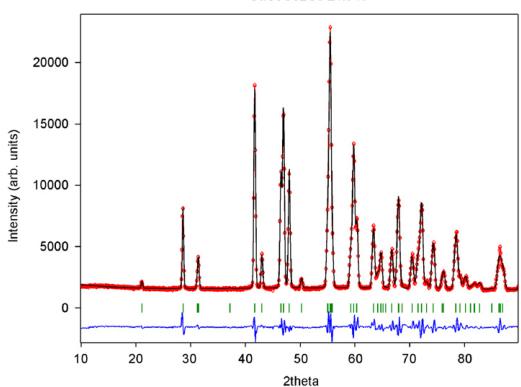
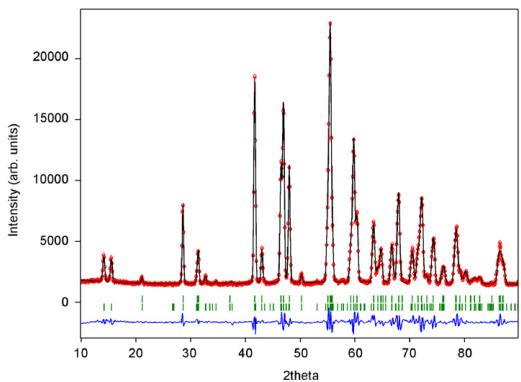
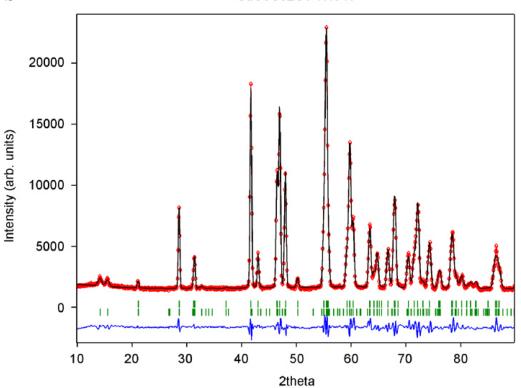
For \( CaCoGe_{2}O_{6} \) there is also a significant contraction of the lattice along the a-axis (Table 4). Additional Bragg reflections appear in the neutron powder diffraction pattern below the magnetic ordering temperature and as in \( CaFeSi_{2}O_{6} \) the most prominent reflections are (100) and (010). The magnetic unit cell coincides with the atomic cell. The onset of magnetic ordering in the neutron diffraction data is observed between 17.3 and 17.8 K. As an example neutron powder diffraction profiles for \( CaCoGe_{2}O_{6} \) at different temperatures are shown in Fig. 8.
a

Fig. 5. Polyhedral representation of the atomic and magnetic structure of hedenbergite at 1.4K in a view onto the b-c plane (a); (b and c) give the possible magnetic interaction pathways with J = interaction within the chain and \( J_{1} = interaction between two neighbouring chains involving one tetrahedron, dashed lines correspond to the smallest distance between neighbouring M1 cations, the thick lines display the \( J_{1} \) interaction; only the \( Fe^{2+} \) cations and \( SiO_{4} \) tetrahedra are shown for clarity.
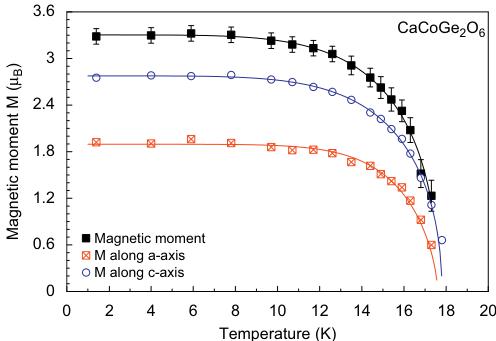
The fits to the temperature dependence of the intensity data of the \( (010) \) and \( (100) \) with the powder law \( I_{hK}(T)=\mathbb{C}[1-(T/T_{N})^{2}]^{c} \) [34] yield a critical exponent of \( \beta=0.44(2) \) and \( T_{N}=17.7(3) \) K for both Bragg reflections. As for hedenbergite, the transition temperature found from neutron diffraction is slightly lower than the one derived from magnetization measurements. Based on the similarity of powder diffraction data in the ordered state, solution of the magnetic structure of \( CaCoGe_{2}O_{6} \) was first tested with the model obtained for \( CaFeSi_{2}O_{6} \) . Indeed the magnetic structure of the Co-germanate can be solved with this model and shows a FM coupling of moments within the M1 chain, neighbouring infinite M1 chains are AFM coupled. The magnetic moments lie within the a-c plane, with the component moment \( M_{z}=2.75(5)\mu_{B} \) being larger than the one along \( M_{\chi}=1.92(4)\mu_{B} \) at 1.4 K. The resulting magnetic moment is \( 3.28(5)\mu_{B} \) , a value close to the theoretical spin-only value of \( Co^{2+} \) . Within the a-c plane, the effective magnetic moment forms an angle of \( 54.2^{\circ} \) with the a-axis and \( 50.6^{\circ} \) with the c-axis (Fig. 9); this orientation does not change as a function of temperature. The magnetic structure of the \( CaCoSi_{2}O_{6} \) is rather similar to the one of the Co-germanate. In \( CaCoSi_{2}O_{6} \) the magnetic moments are also aligned within the a-c plane, forming an angle of \( 41^{\circ} \) with the a-axis, the effective moment was found to be \( 3.30\mu_{B} \) [22,23]. A fit to the temperature dependence of the magnetic moment data of \( CaCoGe_{2}O_{6} \) using the power law \( M(T)=M(0)[1-(T/T_{N})^{2}]^{\beta} \) yields \( T_{N}=17.7(2) \) , \( \alpha=3.65(3) \) and \( \beta=0.44(1) \) . A fit in the critical region \( T_{N}-10K \) only gives a critical exponent of \( \beta=0.37(2) \) . From this the magnetic ordering in \( CaCoGe_{2}O_{6} \) can clearly be described within a 3D model also.
Similar to hedenbergite, structural parameters in \( CaCoGe_{2}O_{6} \) display discontinuities close to the magnetic phase transition. These, however, are not as distinct as in hedenbergite. While the Co–O2 bond length remains almost constant, both Co–O1 bond lengths become shorter in the vicinity of the magnetic phase transition. This also is reflected in the average Co–O bond length. The Co–O1–Co angle is \( 95.1^{\circ} \) , which is the largest value of all compounds investigated here, and it shows no detectable variation with temperature. Some distinct non-linear temperature dependencies are found for the Co–Co interatomic distances: Co–Co atoms within the M1 chain move closer to each other (Fig. 10a), while the shortest distance between Co atoms of two neighbouring chains becomes larger (Fig. 10b). This is opposite to the trend found in hedenbergite. Individual and average Ge–O



Fig. 6. Non-linear temperature-dependent variations of selected structural parameters at the magnetic ordering transition in hedenbergite \( CaFeSi_{2}O_{6} \) . (a) Two out of the three individual Fe–O bond lengths, (b) interatomic Fe–Fe distance within the M1 chain and (c) interatomic distance between two neighbouring M1 chains. Lines fitted to the data are guides to the eye only.

Fig. 7. Temperature dependence of the unit cell volume in synthetic \( CaCoGe_{2}O_{6} \) as extracted from the neutron diffraction data (lines fitted to the data are guides to the eye).
bond lengths both show a slight increase with temperature, the O3–O3–O3 bridging angle decreases. For the Ca–O bonds no clear trends could be found.
3.2.3. CaNiGe₂O₆
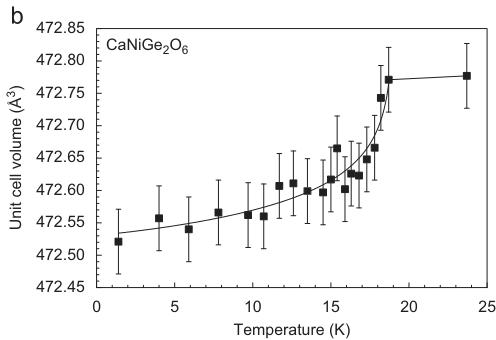
For \( CaNiGe_{2}O_{6} \) , the neutron diffraction experiments were performed in a temperature range between 1.4 and 23.7 K. As for the two previous compounds, some non-linear variations of lattice parameters are observed in the vicinity of the magnetic phase transition, most evident for the b- and c-parameters, with the unit cell of the magnetically ordered phase becoming shrunk (Fig. 11).
The differences in unit cell volumes between the ordered and non-ordered state however are about 1/2 of the ones in \( CaCoGe_{2}O_{6} \) and \( \sim1/3 \) of the ones in \( CaFeSi_{2}O_{6} \) . Additional reflections appear in the neutron powder diffraction pattern of \( CaNiGe_{2}O_{6} \) between 18.7 and 18.2 K, the most prominent ones are again (100) and (010). The fits to the temperature dependency of the intensity data of the (010) and (100) with the power law used above yield a critical exponent of \( \beta = 0.44(2) \) and \( T_{N} = 17.7(3) \) K for both Bragg reflections.
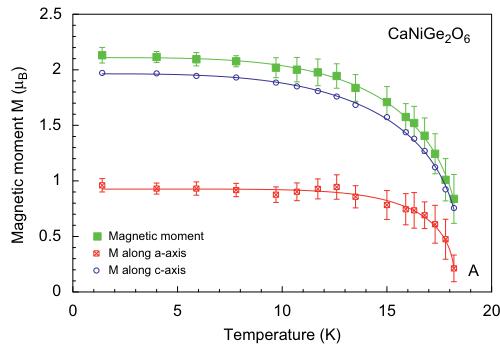
The solution of the magnetic structure of \( CaNiGe_{2}O_{6} \) yielded a FM coupling of magnetic spins within the M1 chains and neighbouring infinite M1 chains show AFM coupling. This is the spin structure already found for \( CaFeSi_{2}O_{6} \) and \( CaCoGe_{2}O_{6} \) . The magnetic moments lie within the a-c plane, with the component moment \( M_{z}=1.94(4)\mu_{B} \) being larger than the one along \( M_{x}=0.92(4)\mu_{B} \) at 1.4 K. The resulting experimental magnetic
a

C

b

d

Fig. 8. Neutron diffraction pattern for synthetic \( CaCoGe_{2}O_{6} \) at selected temperatures showing the onset of magnetic ordering by the appearance of additional Bragg reflections. The most prominent ones (100) and (010) are indicated in the plot for the 1.4 K measurement.

Fig. 9. Variations of the magnetic moments in \( CaCoGe_{2}O_{6} \) as a function of temperature fitted with a power law.
moment is \( 2.09(4)\mu_{\mathrm{B}} \) being distinctly lower than the theoretical spin-only value of \( \mathrm{Ni}^{2+} \) ( \( 2.83\mu_{\mathrm{B}} \) ). Within the a-c plane, the magnetic moment forms an angle of \( 63.7^{\circ} \) with the a-axis and \( 41.5^{\circ} \) with the c-axis (Fig. 12). A fit to the temperature dependence of the magnetic moment data of \( CaNiGe_{2}O_{6} \) yield \( T_{\mathrm{N}} = 17.7(2) \) , \( \alpha = 3.65(3) \) and \( \beta = 0.44(1) \) consistent with a 3D ordering.
Among the structural parameters only the Ni–Ni interatomic distances show some non-linear variations with temperature, which, however, are distinctly smaller than the ones found for hedenbergite or \( CaCoGe_{2}O_{6} \) .
3.2.4. CaMnGe_{2}O_{6}
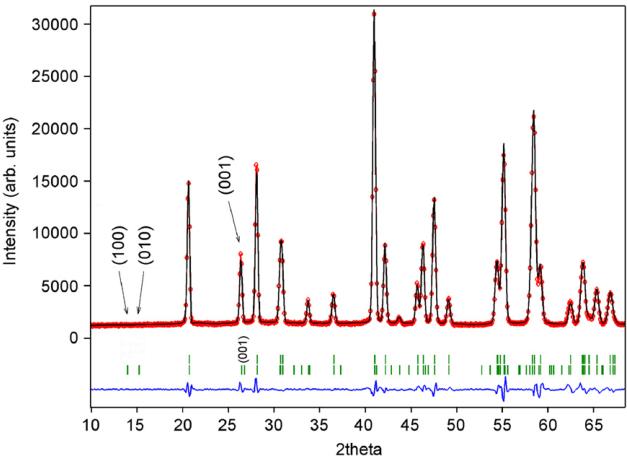
Finally \( CaMnGe_{2}O_{6} \) was investigated by neutron diffraction in a temperature range between 1.4 and 19.4K. In contrast to the previous samples the lattice parameters for \( CaMnGe_{2}O_{6} \) show an almost linear variation with temperature. Only a very small contraction of the unit cell can be deduced from the data at the transition, which is, however, on the order of one standard deviation. Upon cooling first additional Bragg reflections appear in the neutron diffraction pattern at temperatures between 12.7 and 11.8K. The magnetic reflection could be indexed on the basis of the atomic cell; however, it is evident at the first glance that the magnetic spin structure in \( CaMnGe_{2}O_{6} \) must be different to the ones of the three previous compounds: the (100) and (010) reflection are absent, instead, the (001) Bragg reflection is strong.


Fig. 10. Non-linear temperature-dependent variations of selected structural parameters upon magnetic ordering in \( CaCoGe_{2}O_{6} \) : (a) variation of the Co–Co interatomic distance within the M1 chain and (b) Co–Co interatomic distance between two neighbouring M1 chains (lines fitted to the data are guides to the eye).
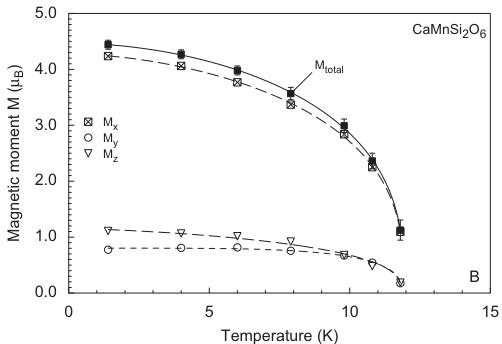
(Fig. 13). Consistent with the strongly negative paramagnetic Curie temperature, a model with AFM ordering of the \( Mn^{2+} \) spins within and between the M1 chains was developed. The Rietveld refinements confirmed this model. The magnetic moments have non-vanishing component along all three crystallographic axes with \( (M_{\mathrm{x}} = 4.24(7)\mu_{\mathrm{B}}, M_{\mathrm{y}} = 0.78(9) \) and \( M_{z} = 1.11(7) \) at 1.4K). This also differs from the three previous compounds where spins are aligned solely within the a–c plane. In \( CaMnGe_{2}O_{6} \) spins are tilted out of the a–c plane by \( 10.3^{\circ} \) at 1.4K, while within the a–c plane they form an angle of \( 14.3^{\circ} \) with the a-axis and \( \sim90^{\circ} \) to the c-axis (Fig. 14). The angle between the magnetic moment and the a-axis decreases slightly with increasing temperature. The total magnetic moment amounts to \( 4.44(8)\mu_{\mathrm{B}} \) at 1.4K being distinctly smaller than the theoretical spin-only value for \( Mn^{2+} \) ( \( 5.92\mu_{\mathrm{B}} \) ). Fitting a power law to the intensity data gives \( T_{\mathrm{N}} = 11.9(5) \) K and \( \beta = 0.32(1) \) and \( 0.34(1) \) for the (001) and the (-201) magnetic Bragg reflection. Similar results were also found for fits to the magnetic moment using the power law given by Blundell [36], i.e. \( T_{\mathrm{N}} = 11.9(2) \) and \( \beta = 0.38(2) \) with d = 3.
4. Conclusion
The clinopyroxenes CaFeSi₂O₆ and CaMGe₂O₆ with M = Ni, Co and Mn show MAGNETIC ordering at temperatures below 35 K.


Fig. 11. Variation of the c-lattice parameter (a) and of the unit cell volume (b) in synthetic \( CaNiGe_{2}O_{6} \) as a function of temperature (lines fitted to the data are guides to the eye).

Fig. 12. Variations of the magnetic moments in \( CaNiGe_{2}O_{6} \) as a function of temperature, fitted with a power law; error bars are not shown for \( M_{z} \) for clarity.
The ordering can be described within a 3D Ising or a 3D Heisenberg model. This is concluded from the appearance of sharp additional Bragg reflections in the neutron diffracting pattern below \( T_{N} \) and from the critical exponents \( \beta \) , being between 0.3 and 0.4 for all compounds.

Fig. 13. Powder neutron diffraction pattern of CaMnGe_{2}O_{6} at 1.4 K. Positions of magnetic Bragg reflections (100), (010) and (001) are labelled.

Fig. 14. Variations of the magnetic moments in CaMnGe_{2}O_{6} as a function of temperature, fitted with a power law.
Major magnetic characteristics (paramagnetic Curie temperature, Neel temperature) of analogue silicate and germanate compositions differ. The most prominent difference between silicate and germanate compounds lies in the tetrahedral site. The \( \langle T-O\rangle \) bond lengths is 1.638 Å in hedenbergite, while it is 1.750–1.758 Å in the germanate compounds. The substitution of \( Si^{4+} \) by \( Ge^{4+} \) results in an increased a- and c-lattice parameter, while b is similar in silicates and germanates (Table 2 and [21]). In order to accommodate the large \( GeO_{4} \) tetrahedra, the tetrahedral chain is distinctly more kinked in the germanate (= smaller O3–O3–O3 bridging angle). Additionally by kinking, the lateral size requirement of the tetrahedral chain is decreased along b. Thus the additional space requirement of the Ge atoms is compensated along b and the b-lattice parameters are very similar for silicates and germanates. As a consequence of the increased size of the \( GeO_{4} \) tetrahedral chain, to which the octahedral chain is attached via common O2 oxygen atoms (apices of the tetrahedra), the separation of individual octahedral M1 site increases distinctly. While in \( CaCoGe_{2}O_{6} \) the M1–M1(inter) atomic distance is \( 5.860(1)\mathring{A} \) 298 K, it is \( 5.566(1)\mathring{A} \) only in the analogous silicate [21]; a similar difference is reported by Redhammer [21] for the Ni-compounds ( \( \Delta = 0.225\mathring{A} \) ). This change most probably affects the magnetic interaction. Within the M1 chain, the M1–M1 interatomic distances also become larger in the germanates by \( \sim0.06\mathring{A} \) , and the M1–O–M1 angle involving the inter-chain coupling J increases by \( \sim1.4^{\circ} \) from analogous silicates to the germanates. These different separations certainly also influence the magnetic properties of silicate and germanate pyroxenes.
All four compounds show a contraction of the unit cell upon cooling through the magnetic phase transition. The most distinct contraction is found for hedenbergite \( CaFeSi_{2}O_{6} \) , followed by \( CaCoGe_{2}O_{6} \) , the smallest contraction is shown by \( CaMnGe_{2}O_{6} \) . Correspondingly, alterations in structural parameters are most evident for hedenbergite, and only small ones are detected for \( CaMnGe_{2}O_{6} \) . Upon magnetic ordering Fe atoms in hedenbergite are displaced along b so that the Fe–Fe distance within the M1 chain increases upon ordering. Contrarily Fe atoms attract each other between two interacting neighbouring chains along \( J_{1} \) and the interatomic distance between two interacting Fe atoms in two next nearest chains is reduced. Similar behaviour can be detected in the \( Ni^{2+} \) and \( Mn^{2+} \) compounds while in \( CaCoGe_{2}O_{6} \) the reverse change is observed and \( Co^{2+} \) are displaced in opposite direction along b.
The Neel temperature is highest in \( CaFeSi_{2}O_{6} \) and decreases towards \( CaMnGe_{2}O_{6} \) . A rough negative correlation is observed between the Neel temperature and the M1–M1 interatomic distances (inter/intra) for the samples of this study. However it has to be noted that for the silicate series (Ni, Co, Fe) such a correlation is not valid. Moreover, while \( CaCoSi_{2}O_{6} \) shows magnetic ordering below 10K, the analogue germanate has \( T_{N}=18.3K \) (from susceptibility data); for the Ni-compounds magnetic ordering temperatures are similar even if the germanates displays distinctly larger distances between interacting cations.
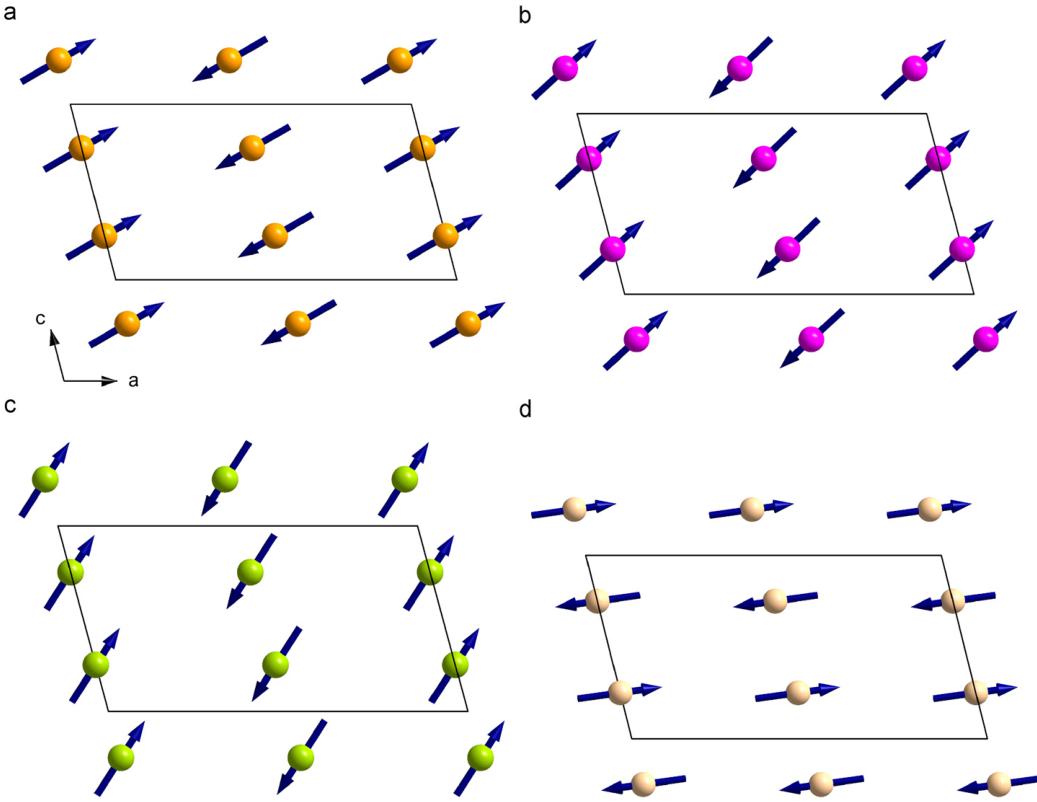
The magnetic structures of the Fe, Co and Ni compounds are quite similar, with a collinear FM coupling of spins within and an AFM coupling between the infinite M1 chains. The magnetic moments are aligned within the a–c plane with no component along b. This is evidently implied from the appearance of \( (0k0) \) reflections with \( k=2n+1 \) (010 reflection in the present case).

Fig. 15. Comparison of the spin structures for (a) CaFeSi₂O₆, (b) CaCO₆e₂O₆, (c) CaNiGe₂O₆ and (d) CaMnGe₂O₆ at 1.4 K within the a–c plane.
With decreasing size of the M1 cation ( \( Fe^{2+} \rightarrow Ni^{2+} \) ) spins rotate away from the a-axis towards c (Fig. 15).
While similar spin structures are were found for the Fe, Co and Ni compounds, the overall magnetic character changes from hedenbergite to \( CaNiGe_{2}O_{6} \) (changing paramagnetic Curie temperature \( \theta_{P} \) ). The net magnetic property in the clinopyroxenes is the sum of the competition of the inter- and intra-chain coupling of spins. While the positive \( \theta_{P} \) in \( CaFeSi_{2}O_{6} \) and \( CaCoGe_{2}O_{6} \) evidences as strong FM interaction within the M1 chain, which dominates the AFM coupling between the chains ( \( J > J_{1} \) ), in \( CaNiGe_{2}O_{6} \) the coupling between the chains dominates the in-chain one ( \( J < J_{1} \) ). Whether the FM coupling becomes very weak, or the AFM coupling very strong, cannot be deduced from the experimental data. As the chain separation becomes smaller in \( CaNiGe_{2}O_{6} \) , this could indicate an increase in the strength of \( J_{1} \) . \( CaMnGe_{2}O_{6} \) is different to the three compounds as it shows complete AFM ordering consistent with the strongly negative \( \theta_{P} \) ; the absence of (0k0) reflections indicates a magnetic moment along b also and spins are inclined from the (a–c) plane (Fig. 15). So even if the M1–O–M1 angle is close to 90°, the Goodenough-Kanamori rules are [37] obeyed here, as e.g. also in LiFeSi₂O₆ [12].
The experimental magnetic moments, determined from susceptibility data, tend to be too high, while for \( Fe^{2+} \) and \( Co^{2+} \) compounds the magnetic moments from neutron diffraction data agree well with the theoretical spin-only values. For \( Ni^{2+} \) and \( Mn^{2+} \) the experimental values from neutron diffraction data however are somewhat smaller than expected.
Acknowledgment
This work was supported by the Austrian “Fonds zur Förderung der wissenschaftlichen Forschung (FWF)” under Grant P19762-N10.
References
[1] M. Cameron, J.J. Papike, Am. Mineral. 66 (1981) 1–50.
[2] R.M. Thompson, R.T. Downs, G.J. Redhammer, Am. Mineral. 90 (2005) 1840–1851.
[3] M. Isobe, E. Nimoyama, A.N. Vasil'ev, Y. Ueda, J. Phys. Soc. Jpn. 71 (6) (2002) 1423–1426.
[4] G.J. Redhammer, H. Ohashi, G. Roth, Acta Crystallogr. B 59 (2003) 730–746.
[5] J.L. Gavilano, S. Mushkolaj, H.R. Ott, P. Millet, F. Mila, Phys. Rev. Lett. 85 (2) (2000) 409–412.
[6] M.D. Lumdsen, G.E. Granroth, D. Mandrus, S.E. Nagler, J.R. Thompson, J.P. Castellan, B.D. Gaulin, Phys. Rev. B 63 (14) (2000) R9244–R9247.
[7] P. Vonlanthen, L.B. Tanaka, A. Goto, Phys. Rev. B 65(21) (2002) Art. No. 214413.
[8] Y. Sasago, K. Hase, K. Uchinokura, M. Tokunaga, N. Miura, N. Phys. Rev. B 52 (1995) 3533–3537.
[9] A. Zheludev, G. Shirane, Y. Sasago, M. Hase, K. Uchinokura, Phys. Rev. B 53 (17) (1996) 11642–11646.
[10] W. Valenti, T. Saha-Dasgupta, C. Gros, Phys. Rev. B 66 (5) (2002) 054426.
[11] G.J. Redhammer, G. Tippelt, M. Merz, G. Roth, W. Treutmann, G. Amthauer, Acta Crystallogr. B 61 (2005) 367–380.
[12] G.J. Redhammer, G. Roth, W. Paulus, G. André, W. Lottermoser, G. Amthauer, W. Treutmann, B. KoppelhuberBitschnau, Phys. Chem. Miner. (2001) 337–346.
[13] M. Isobe, Y. Ueda, A.N. Vasiliev, T.N. Voloshok, O.L. Ignatchik, J. Magn. Magn. Mater. 256 (2003) 125–127.
[14] B. Pedrini, S. Wessel, J.L. Gavilano, H.R. Ott, S.M. Kazakov, J. Karpinski, Eur. Phys. J. B 55 (2007) 219–228.
[15] A.N. Valliev, A.N. Ignatchik, A.N. Sokolov, Z. Hiroi, M. Isobe, Y. Ueda, JEPT Lett. 78 (9) (2003) 551–554.
[16] A.N. Valliev, A.N. Ignatchik, A.N. Sokolova, Z. Hiroi, M. Isobe, Y. Ueda, Phys. Rev. B 72 (2005) 012412, (4pp.).
[17] S.V. Streltsov, D.I. Khomskii, Phys. Rev. B 77 (2008) 064405, (11pp.).
[18] S. Jodlauk, P. Becker, J.A. Mydosh, D.I. Khomskii, T. Lorenz, S.V. Streltsov, D.C. Hezel, L. Bohaty, J. Phys. Condens. Matter 19 (2007) 432201, (9pp.).
[19] A. Wiedenmann, J.R. Regnard, Solid State Comm. 57 (7) (1986) 499–504.
[20] E. Baum, W. Treutmann, W. Lottermoser, G. Amthauer, Phys. Chem. Miner. 24 (1997) 294–300.
[21] G.J. Redhammer, Habilitation Thesis, RWTH, Aachen, Germany, 2001, 420pp. (in German).
[22] G. Durand, S. Vilminot, A. Rabu, A. Derory, J.P. Lamboour, E. Ressouche, J. Solid State Chem. 124 (1996) 374–380.
[23] E. Untersteller, R. Geray, W. Paulus, W. Treutmann, Z. Krist. Suppl. Issue 12 (1997) 70.
[24] G.J. Redhammer, G. Amthauer, G. Roth, G. Tippelt, W. Lottermoser, Am. Mineral. 91 (2006) 1271–1292.
[25] J. Rodrigues-Carvajal, CPD Newslett. 26 (2001) 12–19.
[26] G. Cagliotti, A. Paoletti, F.P. Ricci, Nucl. Istrum. 3 (1958) 223–228.
[27] J.M.D. Coey, S. Ghose, Solid State Comm. 53 (2) (1985) 143–145.
[28] G. Grodzicki, G.J. Redhammer, M. Reissner, W. Steiner, G. Amthauer, Am. Mineral. 2008, under review.
[29] R. Geray, Doctoral Thesis, University of Marburg/Lahn, Germany, 1990, 98pp.
[30] A. Weiss, H. Witte, H. Magnetochemie, Grundlagen und Anwendungen, Wiley-VCH, 1973, 280pp.
[31] G.J. Redhammer, G. Roth, Z. Kristallogr. 217 (2002) 1–10.
[32] G.J. Redhammer, G. Roth, Z. Kristallogr. 219 (2004) 278–294.
[33] G.J. Redhammer, G. Roth, Z. Kristallogr. 219(2004) 585–605.
[34] K. Hagdorn, D. Hohlwein, J. Ihringer, K. Knorr, W. Prandl, H. Ritter, H. Schmid, T. Zeiske, Eur. Phys. J. Condens. Matter B 11 (1999) 243–254.
[35] S.J. Blundell, C.A. Steer, F.L. Pratt, I.M. Marshall, W. Hayes, R.C.C. Ward, Phys. Rev. B 67 (2003) 224411.
[36] S.J. Blundell, Magnetism in Condensed Matter, Oxford University Press, Oxford, 2001, (238pp.).
[37] J.B. Goodenough, Magnetism and the Chemical Bond, Interscience, New York, 1983.