mation was investigated by solving exactly the complete \( (6\times4) \) chromium-aluminum energy-level problem and comparing this exact solution with the additive approximation. The energy differences for the transitions in question were the same to within about 1%, which is a negligible difference.

The second approximation is that the nuclear spins are uncoupled from one another. The error in assuming this would be of the order of the ratio of the nuclear magnetic moment to the \( Cr^{3+} \) magnetic moment or about \( \mu_{n}/\mu_{e}=(1837)^{-1} \) . Thus, the calculation of the linewidth should be reasonably accurate.

The broadening mechanisms discussed above thus inadequately explain the difference between the observed and calculated linewidth variation. In particular, strain and electric field effects, which are often mentioned in connection with broadening of the \( \theta=0^{\circ} \) EPR lines, do not appear to be present in good dilute Verneuil ruby.

In any case, clearly the major part of the broadening is caused by the aluminum hyperfine interaction.

V. CONCLUSIONS

The second moment of an EPR line broadened by nuclear hyperfine interaction can be obtained using Eq. (24) if the energy eigenvalues and eigenfunctions of the nuclei in the presence of the paramagnetic ion are known. The paramagnetic ion need not have a simple spin-level structure.

Applying this calculation to the \( Cr^{3+} \) ion in dilute ruby, the major part (70–80%) of the anisotropic linewidth broadening is found to be caused by strong (super) hyperfine interactions with 13 surrounding aluminum nuclei. The EPR line shape of the \( Cr^{3+} \) ion, strongly interacting with the aluminum nuclei, is calculated by a Monte Carlo method and is found to be Gaussian, in agreement with experimental results. Consequently, the calculation of the second moment is adequate to describe the line. Strains, electric field effects, dislocations, broadening by remote nuclei, and calculational approximations do not appear to account for the additional 20–30% broadening unexplained by the hyperfine mechanism.

ACKNOWLEDGMENTS

The author would like to thank Professor Yeong W. Kim, whose support and assistance made possible the preliminary work for this paper; Neal D. Wilsey, who pointed out Eq. (8); and Bruce J. Faraday for proofreading the paper.

PHYSICAL REVIEW B

VOLUME 1, NUMBER 7

1 APRIL 1970

Magnetic Structure of Magnesium Chromite \( ^{*} \)

H. SHAKED,† J. M. HASTINGS, AND L. M. CORLISS Chemistry Department, Brookhaven National Laboratory, Uplon, New York 11973 (Received 6 October 1969)

The magnetic structure of the normal cubic spinel \( MgCr_{2}O_{4} \) ( \( a_{0}=8.335\ \AA \) ) was investigated by means of neutron diffraction. Two distinct transitions to magnetically ordered states were found at \( \sim16 \) and \( \sim13.5^{\circ}K \) . The reflections associated with the \( 16^{\circ}K \) transition are explained by a class of noncollinear antiferromagnetic structures with a magnetic unit cell identical with the chemical cubic unit cell. The most symmetric of these high-temperature (H) structures belongs to the space group \( P\bar{4}2^{\prime}m^{\prime} \) . The H-structure reflections appeared with different intensities relative to the nuclear reflections in three samples and did not appear at all in two other samples. The low-temperature (L) reflections associated with the \( 13.5^{\circ}K \) transition are explained by either of two nonequivalent noncollinear antiferromagnetic L structures which belong to space groups \( P_{2b}2^{\prime}2^{\prime}2_{1} \) and \( P_{2b}222 \) with a magnetic unit cell \( (2a_{0},2a_{0},a_{0}) \) . The intensities of the L reflections relative to the intensities of the nuclear reflections varied somewhat among the five samples. It is suggested that the H and L structures represent two different phases which coexist below \( 13.5^{\circ}K \) . The intensities of the magnetic reflections (H+L) are accounted for by a magnetic moment of about \( 2.2\mu_{B} \) per \( Cr^{3+} \) .

I. INTRODUCTION

THE compound \( MgCr_{2}O_{4} \) has a normal spinel structure in which the \( Cr^{3+} \) and \( Mg^{2+} \) ions are situated at the B and A sites, respectively. Normal spinels with magnetic ions on the B sites and diamagnetic ions on the A sites make up a class of compounds which are of interest in the study of the B-B interactions. Assuming only first-neighbor interactions in an Ising model, Anderson \( ^{1} \) found a very large degeneracy associated with the lowest energy in this class of compounds. He also showed that this model will, in general, lead to short-range order, whereas long-range order will have to come from interactions with more distant

---

neighbors. Kaplan \( ^{2} \) showed that for nearest-neighbor B-B interactions the minimum Heisenberg energy is the same as the minimum Ising energy. More recently, Dwight and Menyuk \( ^{3} \) pointed out that it takes five distant-neighbor interactions to characterize the Heisenberg energy adequately in this class of compounds. \( ^{4} \) This five-dimensional exchange parameter space consists of regions of stable ferromagnetic, antiferromagnetic, and spiral ground states.

Macroscopic magnetic properties of the ferromagnetic compounds \( CuCr_{2}Se_{4} \) ^{5,6}, \( CuCr_{2}Te_{4} \) ^{5,7}, \( CuCr_{2}S_{4} \) ^{6}, \( HgCr_{2}Se_{4} \) ^{8}, \( CdCr_{2}Se_{4} \) ^{8,9} and \( CdCr_{2}S_{4} \) ^{8} are well known. These compounds form a fairly uniform group with transition temperatures ranging between 460 and 60°K, and \( \Theta \) (asymptotic Curie temperature) between 465 and 135°K. Macroscopic magnetic properties of the antiferromagnetic compounds \( MgV_{2}O_{4} \) ^{10,11}, \( ZnCr_{2}O_{4} \) ^{12–14}, \( MgCr_{2}O_{4} \) ^{11–15}, \( GeFe_{2}O_{4} \) ^{11}, \( GeNi_{2}O_{4} \) ^{11,16}, \( ZnCr_{2}S_{4} \) ^{17}, \( GeCo_{2}O_{4} \) ^{11,16} and \( ZnFe_{2}O_{4} \) ^{18} have also been reported. These compounds exhibit a range \( ^{6} \) to 45°K in \( T_{N} \) (transition temperature) and \( \sim \) 750 to 90°K in \( \Theta \) . Magnetic properties and structures of the spiral compounds \( ZnCr_{2}Se_{4} \) ^{19,20} and \( HgCr_{2}S_{4} \) ^{8,21} are also known. They exhibit transition temperatures of \( \sim \) 20 and \( \sim \) 60°K and positive asymptotic Curie temperatures of 115 and 137°K, respectively.

Neutron-diffraction studies of the spin structures of five of the eight antiferromagnetic compounds mentioned above have been reported. Plumier and Tardieu \( ^{10} \) \( ^{2} \) T. A. Kaplan, Lincoln Laboratory Report No. JA 1608, 1960. \( ^{3} \) K. Dwight and N. Menyuk, Phys. Rev. 169, 435 (1967).

\( ^{4} \) Some other published investigations using 3 and 4 interactions are discussed by these authors.

\( ^{5} \) C. Colominas, Phys. Rev. 153, 558 (1967).

\( ^{6} \) F. K. Lotgering, in Proceedings of the International Conference on Magnetism, Nottingham, 1964 (The Institute of Physics and the Physical Society, London, 1964), p. 533.

7 E. W. Gorter, Philips Res. Rep. 9, 295 (1954).

\( ^{8} \) P. K. Baltzer, H. W. Lehmann, and M. Robbins, Phys. Rev. Letters 15, 493 (1965).

\( ^{9} \) R. C. LeCraw, H. von Philipsborn, and M. D. Sturge, J. Appl. Phys. 38, 965 (1967).

\( ^{10} \) R. Plumier and A. Tardieu, Compt. Rend. 257, 3858 (1963).

\( ^{11} \) G. Blasse and J. F. East, Philips Res. Rep. 18, 393 (1963); see also R. Plumier, Compt. Rend. 263, 173 (1966).

\( ^{12} \) T. R. McGuire, L. N. Howard, and J. S. Smart, Ceramic Age 60, 22 (1952).

\( ^{13} \) E. Whipple and A. Wold, J. Inorg. Nucl. Chem. 24, 23 (1962).

\( ^{14} \) P. Imbert (private communication); F. Varret, A. Gerard, F. Hartmann-Boutron, P. Imbert, and R. Kleinberger, Centre d'Etudes Nucléaires de Saclay (CEN-Saclay), Report No. DPH-G/PSRM/793 (unpublished); F. Hartmann-Boutron, A. Gerard, P. Imbert, R. Kleinberger, and F. Varret, Compt. Rend. 268, 906 (1969). See also R. Plumier and M. Sougi, ibid. 268, 365 (1969).

\( ^{15} \) R. Plumier, Compt. Rend. 267, 98 (1968); R. Plumier, thesis, University of Paris, 1968 (unpublished).

\( ^{16} \) E. F. Bertaut et al., in Proceedings of the International Conference on Magnetism, Nottingham, 1964 (The Institute of Physis and the Physical Society, London, 1964), p. 275.

\( ^{17} \) \( T_{N} \approx 16^{\circ}K \) from neutron diffraction at Brookhaven National Laboratory (unpublished).

\( ^{18} \) J. M. Hastings and L. M. Corliss, Phys. Rev. 102, 1460 (1956).

\( ^{19} \) R. J. Plumier, Compt. Rend. 260, 3348 (1965).

\( ^{20} \) R. J. Plumier, J. Phys. (Paris) 27, 213 (1966).

\( ^{21} \) J. M. Hastings and L. M. Corliss, J. Phys. Chem. Solids 29, 9 (1968).

found a collinear spin structure for \( MgV_{2}O_{4} \) of the type considered by Anderson. \( ^{1} \) Plumier \( ^{15} \) proposed a noncollinear structure for \( MgCr_{2}O_{4} \) , having a cubic magnetic unit cell \( 2a_{0} \) on edge (where \( a_{0} \) is the edge of the chemical unit cell). \( ^{22} \) In the case of \( \mathrm{GeM_{2}O_{4}(M=Co,Ni)} \) , Bertaut et al. \( ^{11,16} \) proposed a spin structure consisting of ferromagnetic sheets (which are coupled antiferromagnetically) perpendicular to a trigonal axis. A complex “banded” spin structure was proposed \( ^{18} \) for \( ZnFe_{2}O_{4} \) .

Magnetic properties of \( MgCr_{2}O_{4} \) were first studied by McGuire et al. \( ^{[12]} \) who reported \( -370^{\circ}K \) and \( 4.0 \) for \( \Theta \) and \( n_{B} \) (effective number of Bohr magnetons), respectively (the spin only value of \( n_{B} \) for \( Cr^{3+} \) is 3.87). Whipple and Wold \( ^{[13]} \) reported a ferromagnetic component of about 0.15 Bohr magnetons at \( 4.2^{\circ}K \) . Blasse and Fast \( ^{[11]} \) later reported \( 15^{\circ}K \) , \( -350^{\circ}K \) , and \( 3.84 \) for \( T_{N} \) , \( \Theta \) , and \( n_{B} \) , respectively, but failed to find a ferromagnetic component at \( 4.2^{\circ}K \) . Plumier \( ^{[15]} \) proposed a class of spin structures that accounted for his \( 4.2^{\circ}K \) neutron-diffraction pattern. These structures are coplanar in the (001) plane, and are consistent with a spiral having a propagation vector \( \mathbf{k}=(1,1,0)/\sqrt{2}a_{0} \) . If one sets the z axis parallel to k, these structures can then be described by a \( C_{2e} \) ( \( C_{c} \) ) lattice. \( ^{[23-26]} \) The most symmetric of these structures belongs to the magnetic space group \( C_{2,2} \) ( \( III_{1}^{15}-B_{2} \) ). \( ^{[23]} \) Recently, Imbert et al. \( ^{[14]} \) have studied the Mössbauer effect in \( Fe^{3+} \) -doped \( MgCr_{2}O_{4} \) at room temperature and at \( T_{N} \) and below. They reported that the full internal field was developed over a narrow range of temperatures in the vicinity of \( 13^{\circ}K \) and concluded that the transition is first order. In our neutron-diffraction study of \( MgCr_{2}O_{4} \) , we have found two new results on which we report in this paper: (i) We observed two magnetic transitions, the first at about \( 16^{\circ}K \) , and the second at about \( 13.5^{\circ}K \) . (ii) We found a spin structure of symmetry \( P\bar{4}2^{\prime}m^{\prime}(III_{11}^{25} \) \( -P\bar{4}2^{\prime}m^{\prime}) \) which accounts for the magnetic reflections associated with the high-temperature transition, and two spin structures of symmetry \( P_{2b}2^{\prime}2^{\prime}2_{1}(III_{18}^{20} \) \( -P_{a}2_{1}2_{2}) \) and \( P_{2b}22(111_{6}^{4}-P_{a}22) \) which account for the magnetic reflections associated with the low-temperature transition.

II. EXPERIMENTAL

Samples

Four powder samples and one single-crystal sample were studied. Sample 1 consisted of the material

\( ^{22} \) This work was published while the present work was in progress.

\( ^{23} \) We use the notation of Opechowski and Guccione (Ref. 24). In parentheses we give the Belov (Ref. 25) notation as used by Kopstik (Ref. 26).

\( ^{24} \) W. Opechowski and R. Guccione, in Magnetism, edited by G. T. Rado and H. Suhl (Academic Press Inc., New York, 1965), Vol. IIa, p. 105.

\( ^{25} \) N. V. Belov, N. N. Neronova, and T. S. Smirnova, Kristallografiya 2, 315 (1957) [Soviet Phys. Cryst. 2, 311 (1957)].

\( ^{26} \) V. A. Koptsik, Shubnikov Groups (Moscow State University Press, Moscow, 1966), in Russian.

---

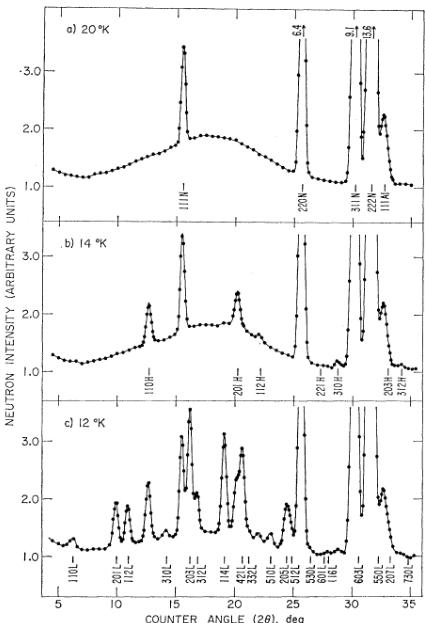
FIG. 1. Neutron ( \( \lambda=1.364\ \AA \) ) diffraction patterns of \( MgCr_{2}O_{4} \) at various temperatures. Nuclear reflections (N) and high-temperature magnetic reflections (H) are indexed on a cubic cell 8.335 Å on edge. Low-temperature magnetic reflections (L) are indexed on a cubic cell 16.670 Å on edge.

described and studied by McGuire et al. \( ^{12} \) Sample 2 was prepared by Whipple and Wold using a “precursor” method. \( ^{18} \) The last three samples were prepared by Kunnmann of Brookhaven National Laboratory in the following way: \( Cr_{2}WO_{6} \) was dissolved in molten \( MgF_{2} \) at \( 1400^{\circ}C \) at constant temperature. The precipitation of \( MgCr_{2}O_{4} \) was accomplished by the slow rate of metathesis of the tungsten trioxide to volatile tungsten

TABLE I. Nuclear reflections, comparison of calculated and observed integrated nuclear intensities for sample 2.

hkl	Calculated \( ^{a} \)	Observed \( ^{b} \)
111 N	2703	2947 (54)
220 N	10 577	11 034 (67)
311 N	20 472	20 923 (71)
222 N	34 025	34 317 (84)
400 N	50 473	49 807 (225)
331 N	4921	4762 (161)
422 N	5651	5215 (128)
511 N, 333 N	34 350	33 934 (225)
440 N	101 800	100 000 (293)

\( ^{a} \) Calculated for the refined nuclear parameters of Table II. \( ^{b} \) The numbers in parentheses are the estimated standard deviations.

TABLE II. Results \( ^{a,b} \) of a least-squares refinement of the nuclear parameters with respect to 9 nuclear reflections for the first three samples.

Sample	Cell	R (%)	u	x (%)	b_{Mg} (10^{-12}cm)
1	Vanadium	1.49	0.3863 (0.0003)	4 (6)	0.55 (0.05)
2	Vanadium	1.70	0.3862 (0.0003)	5 (7)	0.55 (0.06)
3	Aluminum	4.68	0.3868 (0.0006)	-10 (11)	0.51 (0.09)

\( ^{a} \) The numbers in parentheses give bounds on the error resulting from the estimated error in the observations (e.g., Table I).

\( ^{b} \) \( R = [2\sigma_{L}I_{calc}(G) - I_{obs}(G)]^{2}/\sigma^{2}(G)] / [2\sigma_{L}I_{obs}^{2}(G)/\sigma^{2}(G)] \) , where \( \sigma(G) \) is the estimated standard deviation of the Gth reflection; x is the percent inversion. \( b_{Mg} \) is the refined scattering length for the Mg nucleus.

oxyfluoride. In a first such preparation very small (<1 mm) crystallites precipitated and were then ground. Sample 3 consists of this ground material. In a second preparation larger crystallites (up to about 2 mm in size) precipitated. Sample 4 consists of material ground from these crystallites. Sample 5 was a single crystal in the form of an octahedron about 2 mm on edge, taken from the second preparation.

Nuclear Reflections

Room-temperature neutron-diffraction patterns were obtained for the first three samples over an angular range sufficient to include nine nuclear reflections. These reflections were indexed on a cubic unit cell with \( a_{0}=8.335 \) Å. A typical comparison of calculated and observed integrated neutron intensities for the nine reflections is given (for sample 2) in Table I. Least-squares refinements of the nuclear parameters, based on the nine reflections, were performed for each of the first three samples. The refined values are given in Table II. The relatively large R factor in sample 3 is probably related to the difficulty in properly subtracting the aluminum reflections. The refined u values ( \( u\sim0.386 \) ) are close to that found \( ^{27} \) for \( MnCr_{2}O_{4}(u\sim0.389) \) . The refined values of the percent inversion, x, deviate slightly from zero but the errors do not preclude a completely normal ionic distribution. The least-squares values of the scattering length for Mg agree within experimental error with the most recent published \( ^{28} \) value of \( 0.52\times10^{-12} \) cm. The low-temperature nuclear reflections (Fig. 1) exhibit no appreciable deviations in either intensity or angular position from the room-temperature values. Furthermore, no change was detected in these quantities as the sample temperature was lowered from 20 to \( 12^{\circ} \) K.

Magnetic Reflections—Powder Samples

Neutron diffraction patterns at 20, 14, and 12°K obtained with sample 2 are shown in Fig. 1. At 20°K no magnetic reflections are observed. In the 14°K pattern a set of odd-odd-even (ooe) and even-even-odd (eeo)

---

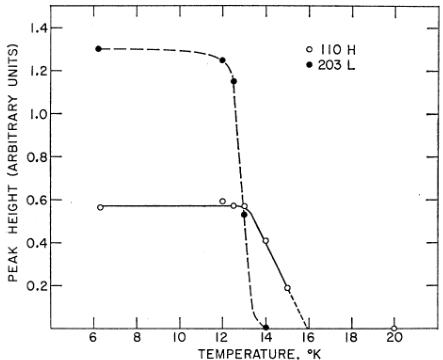
magnetic reflections can be seen which are indexed on a cubic unit cell with \( a_{0}=8.335\ \AA \) . At \( 12^{\circ}K \) additional magnetic reflections are present which can be indexed as ooe and eeo on a cubic cell with \( a_{0}^{\prime}=2a_{0} \) . We have labeled the sets of reflections associated with the high- \( [Fig.1(b)] \) and low- \( [Fig.1(c)] \) temperature transitions as H and L, respectively. It is only the L transition which was reported by previous investigators. The relative intensities among members of the H set or among members of the L set are temperature-independent. The temperature dependence of the intensity of representatives of the H and L sets is shown in Fig. 2. The H and L transition temperatures are estimated from this figure as 16 and \( 13.5^{\circ}K \) , respectively, the former being somewhat uncertain. The temperature dependence exhibits three unusual features: (i) The H structure saturates abruptly at the L transition, but aside from this fact, this structure is totally unaffected by the appearance of the L structure. (ii) The temperature dependence of the sublattice magnetization (square root of the intensity) of the H structure normalized to its \( 6^{\circ}K \) value lies above the Brillouin function characteristic of a second-order phase transition. On the other hand, the temperature dependence does not change abruptly enough to correspond to a first-order phase transition. (iii) The temperature dependence of the L structure, however, is very sharp and may well correspond to a first-order transition (as observed by other authors). \( ^{14} \)

The general features of the intensities of the magnetic reflections from the other samples are shown in Table III where the observed relative intensities of representative reflections of the H and L sets are given. The H structure failed to appear in sample 1, and appeared with different intensities in the other three samples. Some variation in the L structure can also be seen in the table. It should be noted, however, that (i) ratios of reflections within H or L sets were the same in all samples and (ii) transitions and saturation temperatures were also the same in all samples.

Magnetic Reflections—Single Crystal

We have explored the \( [001] \) and \( [111] \) zones of reflections of sample 5 at \( 4.2^{\circ}K \) . All reflections observed were of the L set; reflections of the H set were absent. The zones were explored sufficiently far to include the 770 L and 336 L reflections. The members of a given form of reflection were found to be equivalent (identical integrated intensities) for all forms. This result is characteristic of a crystal in which all magnetic domains are present. That is, from the point of view of the magnetic scattering, the sample is not a single crystal but a polycrystal. In the explorations of the two zones we were able to deduce that eeo reflections with \( h+k=4n \) were systematically absent. This is consistent with our powder pattern [Fig. 1(c)] and in partial agreement with Plumier \( ^{15} \) who reported that the

FIG. 2. Temperature dependence of the peak height above background for the 110 H and 203 L magnetic reflections.

\( h+k=4n \) reflections were systematically absent in both the eeo and ooe reflections. Verification of the extinction rule in the case of powders is only possible for the eeo reflections as shown by the following considerations. If an eeo reflection satisfies the condition \( h+k=4n \) , it follows that the whole form to which the reflection belongs satisfies the same condition. Systematic absences of this type should therefore be observed in powder or multidomain single-crystal data. This, however, is not the case with the ooe group of reflections, where half of the form of reflections always satisfies \( h+k=4n \) , and the other half never does. Consequently, systematic absences of this type cannot be observed in powder or multidomain single-crystal data. In fact, our experimental data did not exhibit any systematic absences in the ooe group of reflections.

III. SEARCH FOR MAGNETIC STRUCTURE

Some Qualitative Remarks

The diffraction patterns of samples 2–4 indicate that an ordered spin arrangement \( (H) \) with the same unit cell as the chemical cell appears at \( \sim16^{\circ}K \) . At \( \sim13.5^{\circ}K \) an additional spin structure \( (L) \) appears with a unit cell of 4 or 8 times the volume of the chemical cell depending on indexing. There are two distinct ways in which the H and L spin structures can coexist: (i)

TABLE III. Observed intensities of 201 L, 112 L, and 110 H relative to 220 N (whose intensity is taken as 1000) for the five samples.

Sample	1	2	3	4	5
hkl
201 L	192	143	161	124	150 \( ^{\circ} \)
112 L	171	121	138	96	115 \( ^{\circ} \)
110 H	0	190	60	20	0

• Corrected to “powder geometry.” These values are possibly affected by extinction.

---

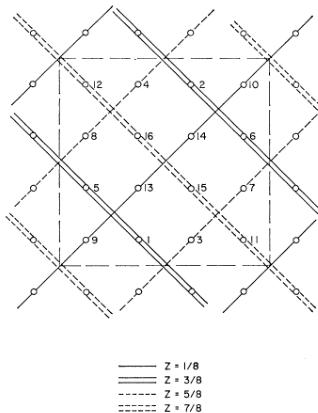
FIG. 3. 001 projection of the \( Cr^{8+} \) positions and the boundary of the cubic chemical unit cell 8.335 Å on edge in \( MgCr_{2}O_{4} \) . The z levels of the positions are given in fractions of the unit cell edge. The numbers refer to a site enumeration scheme used in Appendix C.

as two well-defined phases and (ii) as a single phase. Microscopically speaking, the second case can be further subdivided as follows: (iia) Each spin can be decomposed into two components, one contributing to the H structure and the other to the L structure and (iib) the sites of spins can be divided into two groups, one populated by spins which contribute to the H structure and the other by spins which contribute to the L structure. This last possibility is not very attractive (although not impossible), since it will in general require spins with different magnitudes at different sites. We have made separate searches for possible H and L structures and have considered only those with spins of equal magnitude at all sites, thus essentially eliminating (iib). This approach can lead to a structure of type (iia) only if the individual structures can be combined in a noninterfering way, that is \( S_{i}^{L} \cdot S_{i}^{H} = 0 \) for all sites i. No structures satisfying this orthogonality condition were in fact found. In Sec. IV we offer justification for the two-phase model and a possible explana-

TABLE IV. High-temperature magnetic reflections, comparison of calculated and observed intensities* normalized to 110 H.

hkl	Calculated \( ^{b} \)	Observed
110 H	100	100
201 H	213	224
112 H	67	49
221 H	119	86
130 H	200	187
203 H	82	obsc.
312 H	286	279

• With Lorentz factor and form factor (Ref. 36) removed [I(G) in Appendix A].

\( ^{b} \) Calculated for the spin model shown in Fig. 4.

TABLE V. Lattices \( ^{a} \) allowing the observed low-temperature magnetic reflections.

System	Lattices allowing absent reflections	Lattices not allowing absent reflections
Cubic	P	none
Trigonal	none	none
Tetragonal	\( P^{1}, P^{2} \)	\( P_{P}, I_{P} \)
Orthorhombic	\( P^{1}, P^{2}, C \)	\( C_{P}, P_{C}, F_{C}, I_{P}, P_{2s} \)
Monoclinic	\( P^{1}, P^{2}, C \)	\( C_{p}, P_{C}, P_{2s}, C_{2c} \)
Triclinic	\( P^{1}, P^{2} \)	\( P_{2s} \)

\( ^{a} \) Superscripts 1 and 2 refer to unit-cell translations \( (2a_{0},2a_{0},2a_{0}) \) and \( (2a_{0},2a_{0},a_{0}) \) , respectively.

tion for the observation that the H structure failed to appear in samples 1 and 5 and appeared in different proportions in samples 2–4.

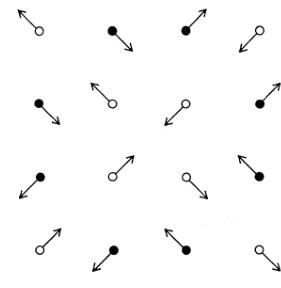
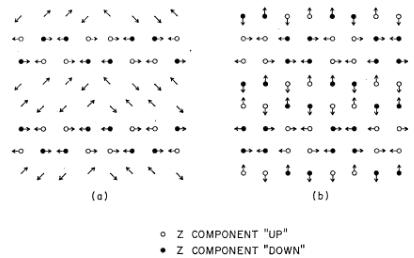
H Structure

It can be shown by direct calculation that no collinear arrangement of spins of equal magnitude on the B sites (Fig. 3) will yield calculated intensities in good agreement with the observed values. The most symmetric of the noncollinear structures giving calculated intensities in reasonable agreement with the observed ones (Table IV) is shown in Fig. 4. This structure belongs to the space group \( P\overline{4}2'm'(\mathrm{III}_{11}{}^{2}55-P\overline{4}2'm') \) . It is a special case of a more general class of structures in the following sense. Let \( \alpha_{i} \) , \( \beta_{i} \) , \( \gamma_{i} \) be the components of a unit spin in the x, y, z directions, respectively, at the ith site for the symmetric structure of Fig. 4 ( \( \alpha_{i}^{2}=\beta_{i}^{2}=\gamma_{i}^{2}=\frac{1}{3} \) ). We define a class of structures in which the ith unit spin is given by

\[ \hat{S}_{i}=\alpha\alpha_{i}\hat{x}+\beta\beta_{i}\hat{y}+\gamma\gamma_{i}\hat{z}. \quad (1) \]

The symmetric structure of Fig. 4 is clearly a member of this class (\(\alpha=\beta=\gamma=1\)). It can be shown by inserting Eq. (1) in the general expression for the structure factor that all structures of this class which satisfy the condition

\[ \alpha^{c}+\beta^{c}=2\gamma^{c}=2 \quad (2) \]

give the same powder diffraction patterns. This means that we may change the x component, say, without changing the diffraction pattern as long as we do not change the spin component in the basal plane. For example, by setting \( \alpha=0 \) , \( \beta=\sqrt{2} \) we obtain a spin structure which is coplanar in (100) and leads to \( J_{\mathrm{calc}}(G) \) (see Appendix A for definition) which are the same as those of the symmetric structure of Fig. 4 for all G. The moment associated with \( Cr^{3+} \) in these structures was calculated from the intensities of sample 2 to be \( 0.7\mu_{B} \) .

L Structure

Magnetic lattices allowing the observed L reflections are listed in Table V. Settings of the lattices relative to the chemical unit cell are given in Table VI. From low-temperature x-ray studies \( ^{14} \) we know that the symmetry

---

TABLE VI. Settings of magnetic lattices.

Lattice	Generators \( ^{a} \)			Number of translationally inequivalent spins per unit volume
P1	(2,0,0)	(0,2,0)	(0,0,2)	128
P \( ^{a} \)	(2,0,0)	(0,2,0)	(0,0,1)	64
C	(1,1,0)	(0,2,0)
P \( _{P} \) , P \( _{C} \)	(1,1,0) \( ^{\prime} \)	(1,1,0) \( ^{\prime} \)		64
I \( _{P} \)	(1,1,0)	(1,1,0)	(1,0,1) \( ^{\prime} \)	32
C \( _{P} \)	(1,1,0) \( ^{\prime} \)	\( (0,1,0) \) \( ^{\prime} \)	(0,0,2)	64
F \( _{C} \)	(1,1,0)	(1,0,1) \( ^{'} \)	\( (0,1,1) \) \( ^{\prime} \)	32
P \( _{2a} \)	(1,0,0) \( ^{\prime} \)	\( (0,2,0) \)	(0,0,1)	32
P \( _{2b} \)	(2,0,0)	\( (0,1,0) \) \( ^{\prime} \)	(0,0,1)	32
P \( _{2a} \)	(1,0,1)	\( (0,2,0) \)
C \( _{2a} \)	(1,1,0)	\( (0,2,0) \)	\( (0,0,1) \) \( ^{\prime} \)		64

• Three basic primitive translations which generate the magnetic lattice, given in the space of three translations parallel to the three edges of the chemical fcc cell. The prime indicates that the translation is followed by spin reversal.

\( ^{b} \) \( P_{2a} \) stands for any of the three lattices \( (s=a,b,c) \) .

at \( 4.2^{\circ}K \) is no higher than tetragonal (Tables V and VI show, on the basis of extinctions, that it indeed could not be trigonal). Since the positions and intensities of nuclear reflections are unaffected by the transition, we assume that atomic displacements, including displacements of the nonmagnetic atoms, are negligible. This implies that the magnetically ordered crystal can not have any symmetry element which is not in the paramagnetic crystal. In other words, the magnetic space group must be a subgroup of the paramagnetic space group which is \( Fd3m1' \) . (This is strictly correct for a second-order phase transition. \( ^{29} \) ) The search \( ^{30,31} \) was restricted to the class of subgroups of \( Fd3m1' \) having unit-cell translations \( (2a_{0},2a_{0},a_{0}) \) or \( (2a_{0},2a_{0},2a_{0}) \) . There are many space groups from cubic down to triclinic in this class of subgroups, a fact which make an exhaustive search impossible. We have therefore conducted a systematic search only on some of the most symmetric of these space groups. The choice of lattice was restricted to \( I_{P} \) which is the most symmetric of those listed in Table V in the sense that it appears in the highest crystallographic system (tetragonal) and that it gives the minimum number of translationally inequivalent spins per unit volume. Table VII lists all such magnetic subgroups of \( Fd3m1' \) in the tetragonal and orthorhombic systems. For the latter system we have included space groups with the \( P_{C} \) lattice since it is equivalent to \( I_{P} \) by rotation through \( \frac{1}{4}\pi \) . These space groups were obtained by noting in the tables of

\( ^{20} \) L. D. Landau and E. M. Lifshitz, Statistical Physics (Addison-Wesley Publishing Co., Inc., Reading, Mass., 1969), p. 437.

\( ^{30} \) The crystallographic (single color) analog of this problem was discussed in its general form by Buerger (Ref. 31). In his notation the paramagnetic structure and the magnetically ordered structure are called basic structure and derivative structure, respectively. Koptisk (Ref. 26) called these (single colored) simply groups and subgroups (they are indeed) and tabulated subgroup of index 2.

\( ^{31} \) M. J. Buerger, J. Chem. Phys. 15, 1 (1947).

○ Z COMPONENT "UP"

● Z COMPONENT "DOWN"

FIG. 4. 001 projection of the symmetrical high-temperature spin model. Symmetry: \( P4\bar{2}^{\prime\prime} \) (III \( _{111} \) \( ^{2b5} \) - \( P4\bar{2}^{\prime\prime} \) m). The atomic positions correspond to those shown in the chemical unit cell of Fig. 3.

Opechowski and Guccione \( ^{24} \) all those chemical space groups with I and F lattices which allow \( I_{P} \) and \( F_{C} \) magnetic lattices in the tetragonal and orthorhombic systems. From this list we eliminated those space groups which could be shown not to be subgroups of \( Fd3m \) (for example \( F_{mmm} \) ). The remaining \( I_{P} \) and \( F_{C} \) space groups are listed in Table VII.

In the exploration of possible magnetic structures individual spin orientations were restricted to the following symmetrical sets of directions: (i) \( \langle100\rangle \) , six directions parallel to cube edges; (ii) \( \langle111\rangle \) , eight directions parallel to cube body diagonals; and (iii) \( \langle110\rangle \) , twelve directions parallel to face diagonals. The exploration was performed with a computer program which assigned all possible permutations of the members of a given symmetrical set to spins unrelated by symmetry. Thus, in \( F_{C}22 \) , eight of the 128 spins in the unit cell are unrelated by symmetry. Choosing the set \( \langle100\rangle \) , for example, the eight spins were assigned all possible combinations of direction \( \pmx \) , \( \pmy \) , \( \pmz \) . In space groups such as \( I_{P}mm2 \) , where the independent

TABLE VII. Tetragonal and orthorhombic magnetic subgroups of \( Fd3m1' \) with \( F_{C} \) and \( I_{P} \) lattices. [Tabulation restricted to subgroups compatible with unit cells \( (2a_{0},2a_{0},a_{0}) \) and \( (2a_{0},2a_{0},2a_{0}) \) ]

System	Space group
Tetragonal	\( I_{P}\bar{4}c^{\prime}2^{\prime}a \)	\( I_{P}\bar{4}c2a \)	\( I_{P}\bar{4}m2a \)
	\( I_{P}\bar{4} \)
Orthorhombic	\( F_{C}22^{\prime}2^{\prime} \)	\( F_{C}22 \)
	\( I_{P}mm2 \)	\( I_{P}mm^{\prime}2^{\prime} \)	\( I_{P}m^{\prime}m^{\prime}2 \)
	\( I_{P}ba2 \)	\( I_{P}ba^{\prime}2^{\prime} \)	\( I_{P}b^{\prime}a^{\prime}2 \)
	\( I_{P}ma2 \)	\( I_{P}ma^{\prime}2^{\prime} \)	\( I_{P}m^{\prime}a^{\prime}2 \)

\( ^{a} \) Supergroup of \( I\bar{P} \) and \( Fc222 \) .

\( ^{b} \) Supergroup of \( Fc222 \) .

---

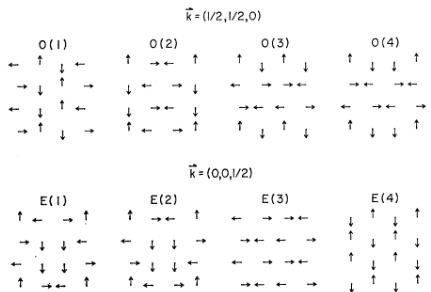
FIG. 5. 001 projections of O and E spin models from which the low-temperature structure (L) can be derived. Only the chemical cells are shown, and the associated wave vectors K are specified.

spins subdivide into groups with different sites symmetries, the three symmetrical sets were assigned separately to each group. In addition, the spin structures were subject to the constraint that all eeo reflections with \( h+k=4n \) must vanish. We did not explore the first four structures in Table VII, since a spin structure invariant under any of these space groups will have to be generated also in the exploration process of its subgroup \( Fc222 \) ( \( III_{21}^{44}-C_{A}222 \) ). This procedure failed to generate a satisfactory structure of orthorhombic symmetry or higher with \( F_{C} \) or \( I_{P} \) lattices. We did, however, find that \( Fc22'2' \) ( \( III_{20}^{87}-C_{A}222 \) ) and \( Fc222 \) ( \( III_{21}^{44}-C_{A}222\) ) generated spin structures, which we designate as O and E, which gave partial fits to the intensities. Structures of type O gave satisfactory agreement with the ooe reflections and zero intensity for the eeo reflections, whereas structures of type E gave the reverse result. The four possible structures of each type are shown in Fig. 5. Some of these structures, but not all, transform like basis vectors for the two dimensional representation, \( \Gamma_{5} \) , of \( P\overline{4}2m \) . For example, the spin structure \( O(4) \) (Fig. 5) corresponds to the basis vector \( \varphi_{22}+\psi_{12}+\psi_{22}^{-1} \) (Appendix C). This fact is interesting since the H structure transforms like a one-dimensional representation, \( \Gamma_{2} \) , of \( P\overline{4}2m \) .

A satisfactory low-temperature \( (L) \) structure can be obtained by combining the O and E structures in such a way as to satisfy the condition \( S_{i}^{0}\cdotS_{r}^{E}=0 \) for all sites i. Combinations obeying this orthogonality condition can be constructed by rotating one type of structure \( _{a} \) (say E) around a body diagonal and adding it to a

TABLE VIII. Magnetic symmetry which results from noninterfering combinations \(O(i)\pm R(i,j)E(j), i, j=1,2,3,4\).

	O(1)	O(2)	O(3)	O(4)
E(1)	P_{2a}2'2'2'1	P_{2a}2'2'2&#*1	P_{2b}2'2'2&#*1	P_{3b}2'2'2&#*1
E(2)	P_{2a}2'2'2	P_{2a}2'2&#*2&#*1	P_{2b}2'2&#*2&#*1	P_{2b2'2&#*2&#*1
E(3)	P_{2b}222	P_{2b}222	P_{2b}222	P2b222
E(4)	P_{2a}222	P_{2a}222	P_{2a}222	P2a222

TABLE IX. Low-temperature magnetic reflections, comparison of calculated and observed intensities.

hkl	Calculated Model 1b	Model 2a	Observed
			Sample 2 (powder)	Sample 5d (single crystal)
110 L	4	10	10	10
201 L	79	101	104	104
112 L	44	114	107	107
310 L	59	23	28	28
203 L	812	826	780	833
312 L	502	294	279	213
114 L	1000	667	1000	...
330 L	330	333	333	378
421 L	1212	1023	1056	...
332 L	93	114	111	...
510 L	755	79	234	87
314 L	158	158	158	175
205 L	1611	909	1119	704
423 L	220	220	220	...
530 L	731	39	73	110
334 L	20	20	20	...
601 L	147	86	v.w.	76
532 L	36	36	164	58
116 L	114	114	...	...
603 L	586	586	osc.	451
550 L	333	333	osc.	346
207 L	161	161	osc.	140
336 L	114	114	v.w.	106
605 L	688	688	osc.	691
607 L	132	132	v.w.	130
770 L	10	10	osc.	12

• With Lorentz factor and form factor (Ref. 36) removed [L(G) in Appendix A]. Powder intensities normalized to (114L+330 L). Single-crystal intensities normalized to powder intensities at 112 L. \( ^{b} \) Values reported by Plummer for his model, with the form factor (Ref. 36) removed. • Calculated for our model with \( \tan\gamma=1.12 \) , where \( \gamma \) is the angle the spin makes with the 001 plane. • Corrected by the “powder multiplicities.” • Reflection not in the zones explored. structure of the other type (O). All such combinations are enumerated in detail in Appendix B. It should be clear, however, that the combined structure is no longer \( F_{G} \) but rather \( P_{2a} \) (or \( P_{2b} \) ) and the nonzero reflections are therefore ooe and oee (or oee). Detailed examination of the combinations of Table VIII shows that two physically distinct structures are obtained, belonging to \( P_{2b}2'2'2'2 \) ( \( III_{18}^{20}-P_{2,2}2'2 \) ) and \( P_{2b}222 \) ( \( III_{6}^{4}-P_{2,222} \) ). They give identical calculated intensities and are shown in Fig. 6. Although we have obtained these structures  FIG. 6. 001 projections of the two low-temperature spin structures: (a) symmetry \( P_{2b}2'2'2'2 \) ( \( III18^{20}-P_{a}2_{1}2_{2} \) ), (b) symmetry \( P_{2b}222 \) ( \( III_{6}^{4}-P_{\alpha}222 \) ). --- by combining two \( F_{c} \) lattices in the manner described in Appendix B, it should be clear that these structures can be “generated” directly in \( P_{2}b^{2}/2'^{2} \) and \( P_{2}b22 \) . In fact we have explored the spin structures belonging to \( P_{2}b22 \) and have found those structures already listed in Appendix B and no additional ones. Because of the orthogonality of the suitably rotated O and \( E' \) structures, there are no restrictions on the magnitudes of \( S^{E} \) and \( S^{O} \) other than those imposed by the observed intensities. Table IX gives a comparison between calculated and observed intensities. For sample 2 the best fit was obtained with \( S^{E}/S^{O}=1.12 \) and the total spin equal to \( 2.0\mu_{B} \) . ## IV. DISCUSSION We were unable to combine any of the H structures (including the low-symmetry structures) with an L structure in such a way that \( S_{L}^{H}\cdotS_{L}^{o}=0 \) for all sites i. We therefore tentatively assume that the two structures correspond to two coexisting magnetic phases. The results presented in Table III for the first three samples qualitatively support this simple picture inasmuch as the intensity associated with the L structure increases as that for H structure decreases. This model leads to the following relations for sample 2: \[ \sqrt{(x)n_{B}H}=0.7,\quad(1-x)^{1/2}n_{B}l=2.0, \] where x is the fraction of the sample occupied by the H phase and \( n_{B}H \) and \( n_{B}l \) are the magnetic moments in Bohr magnetons associated with the H and L structures. If we require \( n_{B}H=n_{B}l=n_{B} \) , these equations yield 2.2 and 0.23 for \( n_{B} \) and x. This low \( ^{32,33} \) \( n_{B} \) value might occur if some of the chromium ions are in low-spin state, as has been found for chromium ions in some other spinels. \( ^{34} \) The generally low magnetic intensities observed for sample 4 may then be attributed to an increased fraction of low-spin chromium ions. There is however another possible explanation for the low \( n_{B} \) value. The background exhibits a broad peak extending from 8 to 23 degrees in \( 2\theta \) at \( 12^{\circ}K \) where the L structure is already saturated [Figs. 1(c) and 2]. This broad peak does not change even when the sample temperature is lowered to \( 4.2^{\circ}K \) , suggesting a residual disordered spin component. Indeed, sample 4 with the weakest magnetic reflections exhibits a background peak almost twice that shown in Fig. 1(c) for sample 2. Such a component could account for the weaker magnetic reflections in sample 4 as well as for the low \( n_{B} \) value in all samples. On the basis of the data that we have, either or both explanations may apply. Imbert et al. \( ^{14} \) found that the room-temperature quadrupole splitting of the Mössbauer line was 0.34 mm/sec for \( Fe^{3+} \) in \( MgCr_{2}O_{4} \) . At \( 4.2^{\circ}K \) they observed a symmetrical hyperfine spectrum. We wish to show that the L structure is consistent with this observation. \( ^{35} \) The spins of the L structure can be divided into two equal sets: (i) those making an angle of \( 90^{\circ} \) with a trigonal axis and (ii) those making an angle of \( 35^{\circ}16' \) with the same trigonal axis. The appropriate \( (3\cos^{2}\theta-1)/2 \) values are \( \frac{1}{2} \) and \( -\frac{1}{2} \) for the two sets, and the lines will therefore be shifted by 0.17/2 and -0.17/2 mm/sec, respectively. This will indeed lead to a symmetrical pattern with each line split by 0.17 mm/sec, which is less than \( \frac{1}{2} \) of the width of the observed lines. A single-crystal single-domain sample would be useful in confirming the \( P_{2a}(s=a,b,c) \) lattice by observing ooe and oee reflections or cyclic permutations of this pair. Furthermore, a systematic study of the intensities from such a sample would show whether the structure belongs to \( P_{2a}2'2'2_{1} \) or to \( P_{2a}222 \) , which are indistinguishable by powder diffraction. The \( P\overline{4}2^{\prime}m^{\prime} \) space group which we have assigned to the symmetric H structure allows a ferromagnetic component in the z direction. As noted above, Whipple and Wold \( ^{18} \) reported a ferromagnetic component of about 0.15 Bohr magnetons at \( 4.2^{\circ}K \) . Since sample 2, which was prepared in the same way, exhibits the most pronounced H structure, it is very reasonable to speculate that the observed ferromagnetism is associated with this structure. ## ACKNOWLEDGMENTS We wish to thank S. J. La Placa for his kind help with the refinement of the nuclear parameters, W. Kunnmann for the preparation of samples 3–5, and M. Blume for an interesting discussion on the interpretation of the Mössbauer data. ## APPENDIX A: INTENSITIES Magnetic: \[ I_{\mathrm{e a l e}}(G)=\sum_{\mathrm{G}}\quad|\hat{G}\times\mathbf{P}(\mathbf{G})|^{2}, \] \[ \mathbf{P}(\mathbf{G})=\sum_{j}^{\mathrm{e l l}}\hat{S}_{j}e^{i\mathbf{G}\cdot\mathbf{r}_{j}}. \] Nuclear: \[ I_{\mathrm{e a l e}}(G)=\sum_{\mathrm{G}}\mid P(\mathbf{G})\mid^{2}, \] \[ P(\mathbf{G})=\sum_{j}^{\mathrm{e e l l}}b_{j}e^{i\mathbf{G}\cdot\mathbf{r}_{j}}. \] Powder: \[ I_{\mathrm{o b s}}(G)=\mathrm{I n t}(G)\sin\theta\sin2\theta/f^{2}. \] Single crystal: \( I_{\mathrm{obs}}(G)=\mathrm{Int}(G)j(G)\sin2\theta/f^{2} \) \( ^{35} \) The following explanation is due to M. Blume. --- where \[ \begin{aligned}\mathbf{r}_{j}&=x_{j}\hat{e}+y_{j}\hat{\theta}+z_{j}\hat{\alpha},\\\mathbf{G}&=2\pi(h\hat{e}+k\hat{\theta}+l\hat{\alpha})/a_{0},\\\sin\theta&=\lambda\left|\mathbf{G}\right|/4\pi,\end{aligned} \] Int(G) is the integrated neutron count over the Gth reflection, \( S_{j} \) is the spin on the jth site, \( b_{j} \) is the nuclear scattering length at the jth site, x, y, z are the orthogonal basis vectors in direct space, \( x_{j}y_{j}z_{j} \) are the coordinates of the jth site in direct space, \( h, k, l_{are} \) the coordinates of the Gth spot in reciprocal space, \( a_{0} \) is the length of unit cell edge, \( \lambda \) is the neutron wavelength, f is the magnetic form factor, \( ^{36} \) and \( j(G) \) is the multiplicity of the Gth form of reflections. ## APPENDIX B: ORTHOGONAL COMBINATIONS OF O- AND E-TYPE SPIN MODELS The magnetic space groups resulting from all orthogonal combinations of the O- and E-type spin models are listed in Table VIII. These combined structures are all of the form \[ C(i,j)=O(i)\pm R(i,j)E(j),\quad i,j=1,\ldots,4. \] The transformations \( R(i,j) \) are listed in Table X. In working out the structures \( C(i,j) \) we placed the origin at the zero-level lower left corner of the chemical unit TABLE X. R(i,j) for Table VIII.

\( \downarrow \)	1	2	3	4
\( \downarrow \)	1	\( \downarrow \)	\( \downarrow \)	\( \downarrow \)
1	\( \downarrow \)	\( \downarrow \)	\( \downarrow^{2} \)	\( \downarrow^{2} \)
2	\( \downarrow \)	\( \downarrow \)	\( \downarrow^{2}\downarrow \)	\( \downarrow^{2}\downarrow \)
3	\( \downarrow^{2} \)	\( \downarrow^{2} \)	\( \downarrow^{2}\downarrow \)	\( \downarrow^{2}\uparrow \)
4	3	3	3	3

cell (Fig. 3). We then used the following representation for the transformations: simple translations, \(t=(\frac{1}{2},0,\frac{1}{2})\); threefold rotations; \[ \exists=\begin{bmatrix}{{{0}}}&{{{0}}}&{{{P(1)}}} \\{{{P(1)}}}&{{{0}}}&{{{0}}} \\{{{0}}}&{{{P(1)}}}&{{{0}}}\end{bmatrix},\quad\exists^{2}=\begin{bmatrix}{{{0}}}&{{{P(2)}}}&{{{0}}} \\{{{0}}}&{{{0}}}&{{{P(2)}}} \\{{{P(2)}}}&{{{0}}}&{{{0}}}\end{bmatrix}, \] where the matrices transform the spin components and the \(P(i)\), \((i=1,2)\) are the appropriate site permutation. To obtain all the structures which are equivalent to a given structure of symmetry, say \(P_{2a}222\), we first note that the \(P_{2b}222\) structures are equivalent. So Table VIII gives us 32 equivalent structures (including negatives). These become 96 equivalent structures through body-diagonal threefold rotation. The magnetic structures shown in Figs. 6(a) and 6(b) correspond to \( O(4)+3^{2}E(1) \) and \( O(3)+3^{2}E(3) \) , respectively. ## APPENDIX C: IRREDUCIBLE REPRESENTATIONS OF P42m In Table XI we give the irreducible representations (i.r.) of \( P\overline{4}2m \) associated with \( \mathbf{k}=(0,0,0) \) , \( (\frac{1}{2},\frac{1}{2},0) \) , and \( (0,0,\frac{1}{2}) \) . In Tables XII and XIII we list the basis vectors \( \varphi_{ij} \) and \( \psi_{ij} \) for the two-dimensional representation, \( \Gamma_{b} \) , in the spin spaces of the \( 8(o) \) and \( 4(n) \) sites of \( P\overline{4}2m \) , respectively. The first subscript enumerates the sub- TABLE XI. Irreducible representations of \( P\overline{4}2m \)

	1	\( \overline{4} \)	\( 2_{s} \)	\( \overline{4}^{3} \)	\( 2_{x} \)	\( m_{1} \)	\( 2_{y} \)	\( m_{2} \)
\( \Gamma_{1} \)	1	1	1	1	1	1	1	1
\( \Gamma_{2} \)	1	1	1	1	-1	-1	-1
\( \Gamma_{3} \)	1	-1	1	-1	1	-1	-1
\( \Gamma_{4} \)	1	-1	1	-1	-1	1	-1	1
\( \Gamma_{b} \)	\( \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} \)	\( \begin{bmatrix}0 & -1 \\ 1 & 0\end{bmatrix} \)	\( \begin{bmatrix}-1 & 0 \\ 0 & -1\end{bmatrix} \)	\( \begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix} \)	\( \begin{bmatrix}1 & 0 \\ 0 & amp; -1\end{bmatrix} \)	\( \begin{bmatrix}0 & 0 \\ 1 & 0\end{bmatrix} \)	\( \begin{bmatrix}- & 1 \\ 1 & 0\end{bmatrix} \)	0

TABLE XII. Basis vectors for \( \Gamma_{b} \) in the spin space of the \( 8(o) \) sites in \( P\overline{4}2m \) .

Basis vector	Site 1	2	3	4	5	6	7	8
\( \varphi_{11} \)	x	x	x	x	y	y	y	y
\( \varphi_{12} \)	\( \bar{x} \)	\( \bar{x} \)	x	x	y	y	y	y
\( \varphi_{21} \)	y	y	y	y	x	x	x	x
\( \varphi_{22} \)	y	y	y	y	\( \bar{x} \)	x	x	x
\( \varphi_{31} \)	y	y	y	y	y	y	y	y
\( \varphi_{32} \)	\( \bar{x} \)	\( \bar{x} \)	x	x	x	\( \bar{x} \)	\( \bar{x} \)
\( \varphi_{41} \)	x	x				x		x	x	x
\( \varphi_{42} \)	y	y	y	y	y	\( \bar{y} \)	y	y
\( \varphi_{51} \)	z	z	z	z	z	z	z	z
\( \varphi_{52} \)	z	z	z	z	z	\( \bar{z} \)	z
\( \varphi_{61} \)	z	z	z	z	z	x	z	z
\( \varphi_{62} \)	z	z	z	z	z	2	z	z

TABLE XIII. Basis vectors for \( \Gamma_{6} \) in the spin space of the \( 4(n) \) sites in \( P\overline{4}2m \) . spaces and the second subscript enumerates the vectors which span the subspace (i.e., \( \varphi_{k1} \) and \( \varphi_{k2} \) are partners in the kth subspace). The site enumeration corresponds to Fig. 3.