| Transition Temperature | 64 K |
|---|---|
| Experiment Temperature | 4.2 K |
| Parent Space Group | Pm-3m (#221) |
| Magnetic Space Group | Im-3m' (#229.143) |
| Magnetic Point Group | m-3m' (32.4.121) |
| Lattice Parameters | 6.908 6.908 6.908 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1002/pssb.2220480229 |
| Reference | P.M. Wintenberger, R. Chamard-Bois, M. Belakhovsky and E.J. Pierre, Physica Status Solidi (b) (1971) 48 705-709. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Dy1 | Dy | 4.98 | 4.98 | 4.98 | 8.63 |
Title
Structure magnétique ordonnée du composé DyCu
Authors
M. WINTENBERGER (a), R. CHAMARD-BOIS (b), M. BELAKHOVSKY (b) et J. PIERRE (a) Affiliations: C.N.R.S. (a) et C.E.N. (b), Grenoble
Materials Studied
DyCu
Key Information
- Crystal structure / space group: CsCl type cubic structure. The magnetic structure analysis considers the crystallographic group Im3m.
- Magnetic ordering type and temperature: Antiferromagnetic, Néel temperature (θ_N) = 64 K.
- Propagation vector(s): k = [1/2, 1/2, 0]
- Magnetic moments:
- Average moment: M = (8.62 ± 0.25) μ_B (for the collinear model).
- Ground state moment for non-collinear structure: J_z = |15/2⟩.
- Ground state moment for collinear structure: J_z = |11/2⟩ or |13/2⟩.
- Lattice parameters: a = 3.454 Å
- Any other critical measured values:
- Crystal field parameter (calculated): Wx = 0.13 K
- Exchange field (deduced from T_N): gμ_B H_ech = 22 K
- Energy difference: The non-collinear configuration is approximately 30 K lower in energy than the collinear configuration.
Synthesis Method
Not available. The paper states that a powder sample of DyCu was studied and that the alloy was diluted in aluminum powder, but it does not describe the method used to synthesize the DyCu compound itself.
Abstract
A powder sample of the compound DyCu has been studied by neutron diffraction. The neutron data leave an indetermination between a collinear magnetic structure with moments pointing along a fourfold axis and a non-collinear structure with moments pointing along the four threefold axes. Crystal field and dipolar energy calculations as well as Mössbauer data ([1]) favour the non-collinear model.
Main Content Summary
The paper investigates the magnetic structure of the DyCu compound using neutron diffraction on a powder sample. DyCu, like other equiatomic rare-earth copper compounds, crystallizes in the cubic CsCl structure and exhibits antiferromagnetic ordering with a Néel temperature of 64 K. The lattice parameter was determined to be 3.454 Å. Neutron diffraction experiments were conducted at 4.2 K and 290 K, with the sample diluted in aluminum powder to mitigate neutron absorption by dysprosium.
The observed magnetic reflections indicate a propagation vector k = [1/2, 1/2, 0], consistent with other similar compounds. Initial analysis of the neutron diffraction data suggested a collinear magnetic structure where moments are aligned parallel to a fourfold axis (Oz) of the magnetic unit cell, yielding an average magnetic moment of (8.62 ± 0.25) μ_B. However, the neutron diffraction pattern alone could not definitively distinguish between this collinear structure (referred to as configuration 'a') and a non-collinear structure (configuration 'b') where moments are oriented along the four threefold axes (<111> directions). Both configurations were found to be equivalent in terms of powder neutron diffraction patterns, isotropic exchange energy, and dipolar energy.
To resolve this ambiguity, the authors performed crystal field calculations and considered existing Mössbauer data. Crystal field calculations, based on a point charge model, indicated that 6th order terms are very weak, and the calculations favored moments along the <111> directions. The exchange energy was found to be comparable to the magnetocrystalline anisotropy energy. A comparison of the reduced ground state energy for both configurations showed that the non-collinear structure (configuration 'b'), with a ground state moment of J_z = |15/2⟩, is approximately 30 K lower in energy than the collinear structure (configuration 'a'), which would have J_z = |11/2⟩ or |13/2⟩.
Furthermore, the electronic ground state determined by Mössbauer effect measurements (from a previous study [1]) was found to be consistent with a J_z = |15/2⟩ state, strongly supporting the non-collinear model. This non-collinear structure, where moments are carried by the four threefold axes, simultaneously satisfies the conditions imposed by both dipolar energy minimization and crystal field considerations.
Conclusion
In summary, the study of the crystal field and Mössbauer effect measurements argue in favor of the non-collinear structure in which the moments are carried by the four threefold axes.
M. WINTENBERGER et al.: Structure magnétique ordonnée du composé DyCu 705
phys. stat. sol. (b) 48, 705 (1971)
Subject classification: 4 and 18.4; 21.1; 21.4
C.N.R.S. (a) et C.E.N. (b), Grenoble
Structure magnétique ordonnée du composé DyCu
Par
M. WINTENBERGER (a), R. CHAMARD-BOIS (b), M. BELAKHOVSKY (b) et J. PIERRE (a)
Le composé DyCu a été étudié par diffraction neutronique sur poudre. Le diagramme observé laisse subsister une indétermination entre une structure colinéaire avec les moments parallèles à un axe quaternaire et une structure non colinéaire avec les moments portés par les axes ternaires. L'étude du champ cristallin, de l'énergie dipolaire et celle de l'effet Mössbauer [1] sont en faveur de ce dernier type de structure.
A powder sample of the compound DyCu has been studied by neutron diffraction. The neutron data leave an indetermination between a collinear magnetic structure with moments pointing along a fourfold axis and a non-collinear structure with moments pointing along the four threefold axes. Crystal field and dipolar energy calculations as well as Mössbauer data \( [1] \) favour the non-collinear model.
1. Introduction
Les composés équiatomiques entre le cuivre et les terres rares du second groupe cristallisent dans la structure cubique du type CsCl. Ces composés sont antiferromagnétiques; la structure magnétique ordonnée a été déterminée par diffraction neutronique pour TbCu [2, 3], HoCu [3] et ErCu [4]. Elle est caractérisée par un vecteur de propagation \( k = \left[\frac{1}{2}, \frac{1}{2}, 0\right] \) , la direction du moment étant parallèle à l'axe c de la maille magnétique \( |2 a, 2 a, a| \) pour TbCu et ErCu et à un axe \( \langle 111 \rangle \) pour HoCu; ces directions sont conformes à celles attendues d'après une étude du champ cristallin.
2. Etude expérimentale
Le composé DyCu a été étudié par diffraction neutronique à 4,2 ct 290 K; le paramètre cristallin vaut \( a = 3,454 \, \AA \) , la température de Néel étant \( \theta_{N} = 64 \, K \) . Pour diminuer la forte absorption des neutrons par le dysprosium, nous avons dilué l'alliage dans de la poudre d'aluminium. Les valeurs des intensités nucléaires et magnétiques obscrées sont données dans les Tablaux 1 et 2; la normalisation a été faite à l'aide des intensités des raies \( \{100\} \) et \( \{110\} \) en adoptant pour longueurs de Fermi \( b_{Dy} = 1,69 \times 10^{-12} \, cm \) et \( b_{Cu} = 0,79 \times 10^{-12} \, cm \) . La raie \( \{111\} \) du composé n'a pu être séparée de la raie \( \{200\} \) de l'aluminium.
3. Structure magnétique
Les indices des raies magnétiques, pris dans la maille chimique, sont de la forme \( h/2 \) , \( k/2 \) , l avec hkl entiers, comme pour les composés avec Tb, Ho ou Er. On peut donc interpréter le diagramme de la même manière, en admettant une structure magnétique colinéaire de vecteur de propagation \( k=\left[\frac{1}{2},\frac{1}{2},0\right] \) . Il est alors possible, à partir des intensités des raies, de conclure que les moments
Tableau 1
Tableau 2
| Indices des raies et valeurs observées (en b) des intensités nucléaires à température ambiante (290 K) | Valeurs des intensités nucléaires et magnétiques (en b) observées à 4,2 K et moments correspondants (en magnétons de Bohr) | ||||
| hkl | Iobs. | Iobs. | (μf)² | μ | |
| 100 | 4,75 | 1/20 | 19,59 ± 0,17 | 66,68 | 8,60 |
| 110 | 73,25 | 1/30 | 4,86 | nucleaire | |
| 111 | — | 1/10 | 11,14 ± 0,12 | 57,63 | 8,73 |
| 200 | 36,90 | 1/20 | 73,80 | nucleaire | |
| 1/20 | 28,72 ± 0,44 | 49,18 | 8,60 | ||
| 1/11 | — | nucleaire | |||
| 1/21 | 33,34 ± 0,33 | 39,84 | 8,53 | ||
| 2/20 | 36,84 | nucleaire | |||
doivent être parallèles à l'axe Oz de la maille magnétique quadratique, comme cela a été trouvé dans le composé DyAg [5]. En utilisant pour Dy³⁺ le facteur de formc f calculé par Blume et al. [6], on trouve un moment moyen \( M = (8,62 \pm 0,25) \mu_{B} \) . Dans la suite nous appellerons à la configuration ci-dessus. Pour cette structure colinéaire la direction Oz est celle d'énergie dipolaire minimum (l'énergie dipolaire peut s'écrire \( E = -1,34 \mu^{2}/a^{3} \) (1 - 3 cos² θ), θ étant l'angle des moments avec Oz); par contre elle n'est pas conforme à ce que prévoient les calculs de champ cristallin, comme on le verra par la suite.
Mais en fait le diagramme de diffraction neutronique implique seulement que les moments magnétiques sont parallèles pour les atomes situés aux sommets et au centre d'un cube d'arcée 2 a, puisque les réflactions obéissent à la condition \( h + k + l = 2n \) , les indices étant maintenant rapportés à ce cube d'arcée 2 a.
Ceci conduit à décrire la structure cristalline et les différentes structures magnétiques possibles à partir du groupe cristallographique \( Im3m \) , où les atomes occupent les positions suivantes:
Dy 8 c (symétrie 3m),
\[ \mathrm{Cu}\quad6b\quad\left(\mathrm{symétric}\frac{4}{\mathrm{m}}\mathrm{mm}\right)\mathrm{et}2a\left(\mathrm{symétrie}\mathrm{m3m}\right). \]
Les calculs de champ cristallin favorisant la direction \( \langle111\rangle \) , on considèrera parmi les configurations possibles celles qui conservent la symétrie cubique. On les obtient de la manière suivante: On attribue aux moments trois composantes \( S_{x} \) , \( S_{y} \) , \( S_{z} \) de même module \( S/\sqrt{3} \) , les modes de propagation des trois composantes se déduisant l'un de l'autre par permutation circulaire; si \( S_{x} \) garde le même signe en passant d'un atome à son voisin le long de 0x, et alterne le long de 0y et 0z, on notera le mode \( (0\pi\pi) \) . Les modes possibles pour \( S_{x} \) sont \( (0\pi\pi) \) , \( (0\pi0\pi) \) et \( (0\pi0) \) .
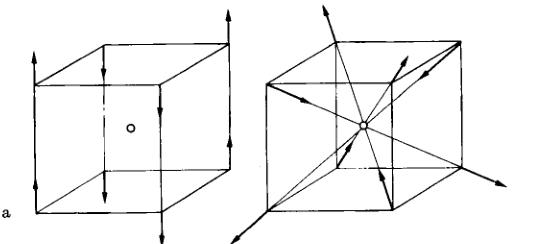
On peut vérifier alors que si l'on adopte pour \( S_{z} \) le mode \( (0\pi\pi) \) , qui conduit à la configuration b de la Fig. 1, le diagramme de diffraction neutronique sur poudre est strictement indiscernable de celui de la configuration a. En effet \( \left|F_{hkl}\right|^{2}=-8f^{2}S_{z}^{2}(1+\cos\pi h)(1-\cos\pi k)(1-\cos\pi l)+\text{permutation circulaire et l'on voit que pour un triplet}\left\{hkl\right\} \) donné \( (h+k+l=2n) \) , la composante \( S_{z} \) contribue seule lorsque c'est l'indice h qui est pair, \( S_{y} \) pour k pair et \( S_{z} \) pour l

Fig. 1. Structures magnétiques a) colinéaire et b) non colinéaire
pair, de sorte que l'intensité totale de la raie est la même que si l'on superposait trois structures colinéaires de type a avec des moments \( S/\sqrt{3} \) . De même si \( S_{x} \) se propage suivant les modes \( (\pi0\pi) \) ou \( (\pi\pi0) \) , les configurations correspondantes sont indiscernables d'une structure colinéaire de même maille que la structure a, mais avec des moments situés dans le plan xy.
Des indéterminations analogues se présentent pour MnTe_{2} [7] et β-MnS [8]. La configuration b a pour groupe magnétique Im3m'.
L'énergie de couplage magnétique isotrope entre un moment \( S_{0} \) ct ses \( \eta_{lemes} \) voisins s'écrit
\[ E=J_{0n}\sum_{i}^{\prime}\left(S_{0x}S_{i x}+S_{0y}S_{i y}+S_{0z}S_{i z}\right). \]
Elle peut se calculer elle aussi comme la somme des énergies de trois structures colinéaires avec des moments \( S/\sqrt{3} \) . Elle a donc la même valeur pour les configurations colinéaires et toutes les configurations dont les moments sont dirigés suivant les diagonales du cube, pourvu que chaque composante alterne suivant deux des directions 0x, 0y, 0z.
Les structures a et b sont donc équivalentes au point de vue diffraction neutronique sur poudre et au point de vue échange isotrope. De plus on peut vérifier que les configurations a et b ont la même énergie dipolaire. D'une façon générale:
\[ W_{\mathrm{D}}=\frac{1}{2}\sum_{j+0}\left[\frac{\mathbf{S}_{0}\cdot\mathbf{S}_{j}}{R_{j}^{3}}-\frac{3}{R_{j}^{5}}\left(\mathbf{S}_{0}\cdot\mathbf{R}_{j}\right)\left(\mathbf{S}_{j}\cdot\mathbf{R}_{j}\right)\right]. \]
\( R_{j} \) est le vecteur joignant un site 0 pris comme origine au site j; si on repère les atomes dans le cube primitif d'arrête a, \( R_{j} \) a des composantes entières et on peut décrire une configuration en associant à chaque composante du moment un vecteur de propagation \( k_{x} \) , \( k_{y} \) ou \( k_{z} \) qui aura une composante nulle et deux composantes demi-entières.
Les termes croisés dans \( W_{D} \) sont de la forme
\[ \sum_{j+0}R_{j\alpha}R_{j\beta}\left(S_{0\alpha}S_{j\beta}+S_{0\beta}S_{j\alpha}\right)=\sum_{j+0}R_{j\alpha}R_{j\beta}S_{0\alpha}S_{0\beta}\left(\mathrm{e}^{2i\pi k_{\alpha}\cdot\mathbf{R}_{j}}+\mathrm{e}^{2i\pi k_{\beta}\cdot\mathbf{R}_{j}}\right) \]
avec \( \alpha \) , \( \beta = x \) , y ou z. \( k_{\alpha} \cdot R \) est nécessairement entier ou demi-entier et l'expression ci-dessus se réduit à
\[ \sum_{j+0}R_{j\alpha}R_{j\beta}S_{0\alpha}S_{00\beta}\left(\cos2\pi k_{\alpha}\cdot\mathbf{R}_{j}\div\cos2\pi k_{\beta}\cdot\mathbf{R}_{j}\right). \]
Si l'on associe les vecteurs \( R_{j} \) et \( R_{j'} \) , de mêmes composantes \( R_{\beta} \) et \( R_{\gamma} \) et dont les composantes \( R_{\alpha} \) sont opposées, les termes trigonométriques ne changent pas de signe et les termes rectangles s'annulent deux à deux.
\( W_{D} \) ne contient que des termes de la forme \( S_{0\alpha} S_{j\alpha} \) ; par conséquent \( W_{D} \) est la somme des énergies dipolaires des configurations colinéaires sur 0x, 0y et 0z de moment \( S/\sqrt{3} \) . La valeur minimum de cette énergie est atteinte lorsque chaque composante \( \alpha \) alterne sur \( \beta \) et \( \gamma \) , c'est-à-dire que la configuration b est parmi toutes les configurations, colinéaires ou non, où les moments sont portés par les diagonales du cube, celle dont l'énergie dipolaire est minimum. Elle permet ainsi de satisfaire simultanément les conditions imposées par l'énergie dipolaire et par le champ cristallin.
Les considérations précédentes s'appliquent à la structure magnétique de DyAg [5].
4. Discussion
Les modes de propagation de la stucture magnétique sont liés aux interactions magnétiques indirectes du type Ruderman-Kittel comme dans les autres composés cités [3].
Le Hamiltonien de champ cristallin s'exprime sous la forme [9]
\[ \mathcal{H}_{\mathrm{c}}=B_{4}O_{4}(\boldsymbol{J})+B_{6}O_{6}(\boldsymbol{J})=W\left[x\left(\frac{O_{4}}{F(4)}\right)+(1-|x|)\left(\frac{O_{6}}{F(6)}\right)\right] \]
où \( O_{4}(J) \) et \( O_{6}(J) \) sont les équivalents opératoires de Stevens.
Un calcul fait par la méthode des charges ponctuelles en adoptant pour charge de la terre rare \( Z_{1} = +3 \) et pour charge du cuivre \( Z_{2} = 0 \) montre que les termes d'ordre 6 sont très faibles par rapport à ceux d'ordre 4 ( \( x \approx -1 \) ), et permet d'évaluer \( W x = 0.13 K \) . Cette valeur est inférieure d'environ 50% à celle que l'on peut déduire de la valeur expérimentale observée pour le composé CcAg [3], toutefois le signe et l'ordre de grandeur sont corrects. L'échange est du même ordre de grandeur que l'énergie magnétocristalline, aussi est-il nécessaire de diagonaliser le Hamiltonien global pour les diverses orientations du moment magnétique. Dans l'approximation de champ moléculaire, si le moment est parallèle à un axe quaternaire [9],
\[ \mathcal{H}=B_{4}\left(O_{4}^{(0)}\right)+5O_{4}^{(4)})-g\mu_{\mathrm{B}}\boldsymbol{J}\cdot\boldsymbol{H}_{\mathrm{e c h.}}, \]

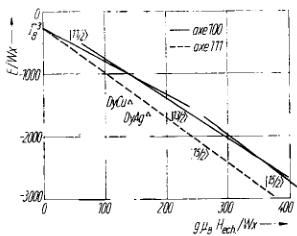
Fig. 2. Energie réduite de l'état fondamental en fonction du rapport de l'échange au champ cristallin
s'il est parallèle à un axe ternaire,
\[ \mathcal{H}=-\frac{2}{3}B_{4}\left(O_{4}^{(0)}-20\sqrt{2}O_{4}^{(3)}\right)-g\mu_{\mathrm{B}}\boldsymbol{J}\cdot\boldsymbol{H}_{\mathrm{e c h}}. \]
où \( H_{ech} \) est le champ d'échange.
La valeur \( g \mu_{B} H_{ech.} = 22 K \) peut être déduite de la température de Néel \( \theta_{N} \) et permet de déterminer l'énergie et la composition des niveaux. Nous avons tracé sur la Fig. 2 l'énergie réduite \( E/W x \) du niveau fondamental en fonction du rapport \( g \mu_{B} H_{ech.}/W x \) de l'énergie d'échange à l'énergie de champ cristallin, et situé les composés DyCu et DyAg selon la valeur calculée pour ce dernier paramètre. Dans le cas de la configuration a, le moment du niveau fondamental est soit \( |11/2\rangle \) , soit \( |13/2\rangle \) , alors qu'il est \( |15/2\rangle \) dans le cas de la configuration b non colinéaire. L'énergie de cette dernière configuration est inférieure d'environ 30 K à celle de la première.
De plus, l'état fondamental électronique a été déterminé par effet Mössbauer [1]: Les valeurs du champ magnétique hyperfin et de l'interaction quadrupolaire ne peuvent s'interpréter avec les valeurs \( J_{z} = |11/2\rangle \) ou \( J_{z} = |13/2\rangle \) de moment du niveau fondamental, mais sont en bon accord avec une valeur \( J_{z} = |15/2\rangle \) .
En résumé, l'étude du champ cristallin et les mesures d'effet Mössbauer militent en faveur de la structure non colinéaire dans laquelle les moments sont portés par les quatre axes ternaires.
Bibliographie
[1] M. BELAKHOVSKY et J. PIERRE, Solid State Commun. 9, 1409 (1971).
[2] J. W. CABLE, W. C. KOEHLER et E. O. WOLLAN, Phys. Rev. 136, A 240 (1964).
[3] J. PIERRE, Proc. 8th Rare Earth Conf., Reno (Nevada) 1970.
[4] W. C. KOEHLER, communication privée.
[5] G. ARNOLD, N. NERESON et C. OLSEN, J. chem. Phys. 46, 4041 (1967).
[6] M. BLUME, A. J. FREEMAN et R. E. WATSON, J. chem. Phys. 37, 1245 (1962).
[7] J. M. HASTINGS, L. M. CORIISS, M. BLUME et M. PASTERNAK, Phys. Rev. B 1, 3209 (1970).
[8] F. KEFFER, Phys. Rev. 126, 896 (1962).
[9] M. T. HUTCHINGS, Solid State Phys. 16, 227 (1964).
K. R. LEA, M. J. M. LEASK et W. P. WOLF, J. Phys. Chem. Solids 22, 1381 (1962).