| Transition Temperature | 192.5 K |
|---|---|
| Parent Space Group | Fm-3m (#225) |
| Magnetic Space Group | Pn-3m' (#224.113) |
| Magnetic Point Group | m-3m' (32.4.121) |
| Lattice Parameters | 6.37000 6.37000 6.37000 90.00 90.00 90.00 |
|---|---|
| DOI | 10.1016/0921-4526(92)90683-j |
| Reference | P. Burlet, F. Bourdarot, J. Rossat-Mignod, J. Sanchez, J. Spirlet, J. Rebizant and O. Vogt, Physica B: Condensed Matter (1992) 180-181 131-132. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Np1 | Np | 1.4 | 1.4 | 1.4 | 2.42 |
Title
Neutron diffraction study of the magnetic ordering in NpBi
Authors
P. Burlet \( ^{a} \) , F. Bourdarot \( ^{a} \) , J. Rossat-Mignod \( ^{a,b} \) , J.P. Sanchez \( ^{a} \) , J.C. Spirlet \( ^{c} \) , J. Rebizant \( ^{c} \) and O. Vogt \( ^{d} \)
\( ^{a} \) CEN-Grenoble, DRFMC/SPSMS/MDN, 85X, 38041 Grenoble Cedex, France \( ^{b} \) Laboratoire Léon Brillouin, CEN-Saclay, 91191 Gif sur Yvette Cedex, France \( ^{c} \) European Institute for Transuranium Elements, Postfach 2340, W-7500 Karlsruhe, Germany \( ^{d} \) E.T.H. Laboratorium für Festkörperphysik, CH 8093 Zürich, Switzerland
Materials Studied
NpBi
Key Information
- Crystal structure / space group: NaCl type structure, cubic group.
- Magnetic ordering type and temperature: Antiferromagnetic, triple-k type-I structure. Néel temperature \( T_{N} = 192.5 \pm 0.1 \) K.
- Propagation vector(s): \( k = |0\ 0\ 1| \) (from abstract), \( k = \langle 0\ 0\ 1 \rangle \), and three equivalent k-vectors \( |0\ 0\ 1| \), \( |0\ 1\ 0| \), \( |1\ 0\ 0| \).
- Magnetic moments:
- Fourier components: \( m_{k} = 1.4 \pm 0.07\mu_{B} \)
- Ordered magnetic moment: \( m = \sqrt{3}m_{k} = (2.48 \pm 0.1)\mu_{B}/Np \) at low temperature.
- Lattice parameters: Not available
- Any other critical measured values:
- Critical exponent \( \beta = 0.31\pm0.02 \) (from abstract)
- Slope \( 2\beta = 0.62 \pm 0.01 \) (from results)
Synthesis Method
The NpBi single crystal \( (1 \times 2 \times 3 \, \text{mm}^{3}) \) was grown by the mineralization technique.
Abstract
The magnetic ordering of NpBi has been determined by neutron diffraction on a single crystal. NpBi orders antiferromagnetically in the triple-k type-I structure \( (k=|\mathbf{0}0|1) \). \( m_{s}//k \) below \( T_{N}=192.5 \) K. The ordered magnetic moment develops at \( T_{N} \) with a critical exponent \( \beta=0.31\pm0.02 \) an increases continuously on cooling to reach a value of \( 2.48\mu_{B}/Np \) at low temperature.
Main Content Summary
This paper investigates the magnetic ordering of NpBi using neutron diffraction on a single crystal. NpBi belongs to the actinide monopnictide series, which crystallize in the NaCl type structure and exhibit peculiar magnetic interactions due to partially localized 5f electrons and hybridization. These interactions are characterized by strong ferromagnetic coupling within (001) planes and weaker interactions perpendicularly, leading to magnetic ordering with wave vectors \( k = |0\ 0\ k| \) and Fourier components \( m_{k}//k \). Multi-k structures, such as double-k or triple-k, are often stabilized to accommodate local moment directions different from the cubic axes.
The NpBi single crystal, measuring \( 1 \times 2 \times 3 \, \text{mm}^{3} \), was grown using the mineralization technique. Neutron diffraction experiments were conducted at the Siloe reactor of CEN-Grenoble, employing a double-axis spectrometer with a neutron wavelength of \( \lambda = 1.54 \, \AA \). The crystal was mounted in a cryomagnet with the \( |1 \, 1 \, 0| \) direction vertical and parallel to the magnetic field.
At low temperatures, superlattice magnetic Bragg reflections were observed, corresponding to the wave vectors \( k = \langle 0\ 0\ 1 \rangle \) and a longitudinal polarization where \( m_{k} \) is parallel to k. The magnetic intensities from the three equivalent k-vectors \( |0\ 0\ 1| \), \( |0\ 1\ 0| \), and \( |1\ 0\ 0| \) were found to be identical, yielding Fourier components \( m_{k} = 1.4 \pm 0.07\mu_{B} \). This implies an ordered Np magnetic moment of \( m = \sqrt{3}m_{k} = (2.48 \pm 0.1)\mu_{B}/Np \), consistent with previous Mössbauer results. The magnetic ordering remains consistent across the entire ordered temperature range below \( T_{N} \). Precise intensity measurements near \( T_{N} \) revealed a Néel temperature of \( T_{N} = 192.5 \pm 0.1 \) K and a critical exponent \( \beta = 0.31 \pm 0.02 \).
Further experiments involved studying the temperature dependence of magnetic intensities under a 4.5 T magnetic field applied along the \( |1\ 1\ 0\rangle \) axis. The intensities from the three equivalent k-vectors remained equal and exhibited the same temperature dependence, indicating the absence of domain motion. This observation is crucial as collinear and double-k structures, which possess tetragonal symmetry, would typically show domain motion under such a field. The preservation of cubic symmetry and the single-domain nature of the triple-k ordering are consistent with the experimental results, thus confirming a triple-k type-I magnetic structure in NpBi. This structure is also found in USb and NpSb, which share similar Néel temperatures. The triple-k type-I ordering is noted for its stability, resisting metamagnetic transitions and requiring strong magnetic fields to overcome its coupling even near \( T_{N} \). The determined critical exponent \( \beta = 0.31 \) aligns with theoretical predictions for a 3d Ising system and is observed in other NaCl compounds of Ce, U, and Np, all characterized by similar anisotropic exchange interactions, though NpSb shows a slightly lower \( \beta \) value of 0.257.
Conclusion
The neutron diffraction study definitively establishes that NpBi orders antiferromagnetically in a triple-k type-I structure, characterized by a propagation vector \( k = \langle 0\ 0\ 1 \rangle \) and longitudinal polarization. The Néel temperature is \( T_{N} = 192.5 \pm 0.1 \) K, and the ordered magnetic moment reaches \( 2.48\mu_{B}/Np \) at low temperatures. The critical exponent \( \beta = 0.31 \pm 0.02 \) is consistent with a 3d Ising system, a characteristic shared with other actinide monopnictides exhibiting similar anisotropic exchange interactions. The triple-k ordering, which preserves the full cubic symmetry, was confirmed by the absence of domain motion under an applied magnetic field, highlighting its inherent stability against metamagnetic transitions. This type-I triple-k structure is common to USb, NpSb, and NpBi, which also share similar Néel temperatures.
Neutron diffraction study of the magnetic ordering in NpBi
P. Burlet \( ^{a} \) , F. Bourdarot \( ^{a} \) , J. Rossat-Mignod \( ^{a,b} \) , J.P. Sanchez \( ^{a} \) , J.C. Spirlet \( ^{c} \) ,
J. Rebizant \( ^{c} \) and O. Vogt \( ^{d} \)
\( ^{a} \) CEN-Grenoble, DRFMC/SPSMS/MDN, 85X, 38041 Grenoble Cedex, France
\( ^{b} \) Laboratoire Léon Brillouin, CEN-Saclay, 91191 Gif sur Yvette Cedex, France
\( ^{c} \) European Institute for Transuranium Elements, Postfach 2340, W-7500 Karlsruhe, Germany
\( ^{d} \) E.T.H. Laboratorium für Festkörperphysik, CH 8093 Zürich, Switzerland
The magnetic ordering of NpBi has been determined by neutron diffraction on a single crystal. NpBi orders antiferromagnetically in the triple-k type-I structure \( (k=|\mathbf{0}0|1) \) . \( m_{s}//k \) below \( T_{N}=192.5 \) K. The ordered magnetic moment develops at \( T_{N} \) with a critical exponent \( \beta=0.31\pm0.02 \) an increases continuously on cooling to reach a value of \( 2.48\mu_{B}/Np \) at low temperature.
NpBi belongs to the homogeneous series of actinide monopnictides MX (M = U, Np, Pu; X = N, P, As, Sb, Bi) which crystallize in the NaCl type structure. In these compounds, due to the partially localized character of the 5f electrons, the hybridization with the p or d electrons leads to peculiar magnetic interactions [1]. A characteristic of these interactions is their anisotropy which consists in strong ferromagnetic coupling in a \( (001) \) plane and much weaker interactions in the perpendicular direction. This results, without any exception, in a magnetic ordering characterized by wave vectors and Fourier components \( k = |0\ 0\ k| \) and \( m_{k}//k \) . The particular value of k depends on the details of the interplane interactions. In many cases a local moment direction, different from the cubic axis, is satisfied by stabilizing multi-k structures; double-k if \( m//\langle1\ 1\ 0\rangle \) and triple-k if \( m//\langle1\ 1\ 1\rangle \) [2].
Since the pioneering work of the Argonne group [3], who studied by powder neutron diffraction the magnetic ordering of some Np monopnictides, the availability of large and good quality single crystals has allowed much progress in the description of the magnetic behaviour of these compounds, such as a detailed description of the nature of the magnetic ordering and the determination of the field versus temperature phase diagrams [4].
The NpBi single crystal \( (1 \times 2 \times 3 \, \text{mm}^{3}) \) was grown by the mineralization technique [5]. It was encapsulated in a sealed double wall aluminium sample holder. The neutron experiments were performed at the Siloe reactor of CEN-Grenoble, using a double axis spectrometer equipped with a moving up counter arm. The crystal was mounted in a cryomagnet with a \( |1 \, 1 \, 0| \) direction vertical and parallel to the magnetic field direction. A neutron wavelength \( \lambda = 1.54 \, \AA \) , provided by an HOPG monochromator and filtered by pyrolitic graphite, was used.
Results and discussion
At low temperatures, superlattice magnetic Bragg reflexions are observed corresponding to the wave vectors \( k = \langle 0\ 0\ 1 \rangle \) and to a longitudinal polarization \( (m_{k} \) parallel to k). The magnetic intensities from the three equivalent k-vectors \( |0\ 0\ 1| \) , \( |0\ 1\ 0| \) and \( |1\ 0\ 0| \) have the same values and give Fourier components \( m_{k} = 1.4 \pm 0.07\mu_{B} \) . This situation can correspond either to a collinear structure, with an equipartition of domains, or to multi-k ordering [6]. In any case the Np ordered moment value is \( m = \sqrt{3}m_{k} = (2.48 \pm 0.1)\mu_{B}/Np \) , which is in good agreement with Mössbauer's results [6].
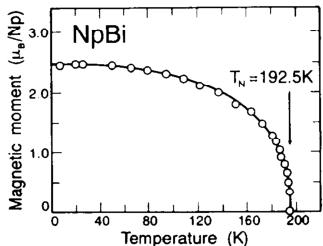
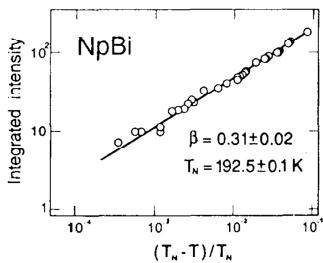
The same magnetic ordering is observed in the whole ordered temperature range below \( T_{N} \) (fig. 1). Accurate intensity measurements in the vicinity of \( T_{N} \) , in the range of reduced temperature \( 10^{-3} < (T_{N} - T) / T_{N} < 10^{-1} \) , have been made. A log–log plot of these intensities versus temperature gives a straight line (corresponding to \( T_{N} = 192.5 \pm 0.1 \) K and a slope \( 2\beta = 0.62 \pm 0.01 \) ) which characterizes the critical exponent \( \beta \) (fig. 2). The temperature dependence of

Fig. 1. Temperature dependence of the Np magnetic moment in NpBi in zero applied field.

Fig. 2. Log-log plot of the magnetic intensities versus reduced temperature \( T_{N}-T/T_{N} \) in NpBi near the ordered temperature.
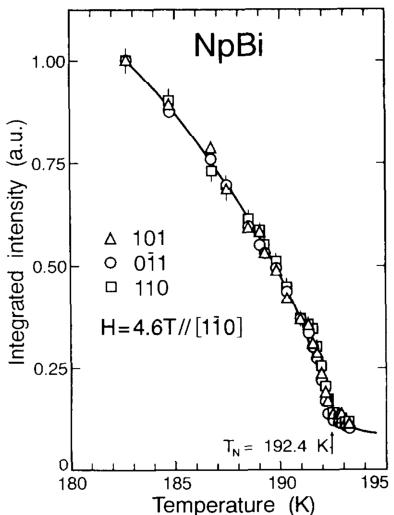
the magnetic intensities has also been studied for a magnetic field of 4.5 T applied along a \( |1\ 1\ 0\rangle \) axis. As shown in fig. 3 the magnetic intensities, arising from the 3 equivalent k-vectors measured on cooling the sample from above \( T_{N} \) , have the same values and the same temperature dependence. This implies the absence of any domain motion. Collinear and double-k structures of tetragonal symmetry give rise to three domains which are not equivalent with respect to this applied field. This situation gives rise to domain motion in a rather small applied magnetic field which

Fig. 3. Temperature dependences of the magnetic intensities in NpBi under a magnetic field \(H=4.5\mathrm{T}\) along the \(|110|\) direction.

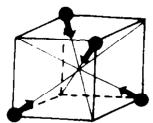
Fig. 4. Multiaxial (triple-k) structure of NpBi.
leads to a change of intensities. The triple-k ordering, which preserves the full symmetry of the cubic group, presents only one domain and the magnetic field cannot have any effect, unless the interaction terms stabilizing the triple k structure were dominated by the Zeeman energy \( (- \chi H^{2}) \) of a collinear structure. The present experimental results then allow us to deduce a triple-k ordering in NpBi. The corresponding multiaxial structure is shown in fig. 4. This triple-k type-I structure is common to USb, NpSb and NpBi. These compounds have similar Néel temperatures (212 K in USb, 199 K in NpSb and 192.5 K in NpBi). The type-I triple-k ordering is very stable because no metamagnetic transition can be induced in the range of experimentally available magnetic field and, moreover, even near to \( T_{N} \) , large fields (H > 5 T) are needed to overcome the coupling resulting in the triple-k ordering [6]. The critical exponent \( \beta = 0.31 \) corresponds to the theoretical one expected for a 3d Ising system and has also been observed in many other NaCl compounds of Ce, U and Np which all are characterized by the same anisotropic exchange interaction [7]. However in NpSb \( \beta = 0.257 \) ; a value much lower than that found in NpBi in spite of their similarities [7].
References
[1] B.R. Cooper, R. Sieman, D. Yang, P. Thamyamballi and A. Banerjea, Handbook on the Physics and Chemistry of the Actinides, Vol. 2, eds. A.J. Freeman and G.H. Lander (North-Holland, Amsterdam, 1985) p. 435.
[2] J. Rossat-Mignod, G.H. Lander and P. Burlet, Handbook on the Physics and Chemistry of the Actinides, Vol. 1, eds. A.J. Freeman and G.H. Lander (North-Holland, Amsterdam), 1984) p. 415.
[3] A.J. Aldred, B.D. Dunlap, A.R. Harvey, D.J. Lam, G.H. Lander and M.H. Mueller, Phys. Rev. B 9 (1974) 3766.
[4] P. Burlet, D. Bonnisseau, S. Quézel, J. Rossat-Mignod, J.C. Spirlet, J. Rebizant and O. Vogt, J. de Phys 49 (1989) C8–469.
[5] O. Vogt and J.C. Spirlet, J. Magn. Magn. Mater. 63 & 64 (1987) 683.
[6] J.P. Sanchez, P. Burlet, S. Quézel, D. Bonnisseau, J. Rossat-Mignod, J.C. Spirlet, J. Rebizart and O. Vogt, Solid State Commun. 67 (1988) 999.
[7] D.L. Jones, W.G. Stirling, G.H. Lander, J. Rebizant, J.C. Spirlet, M. Alba and O. Vogt, J. Phys. Condens. Mat. 3 (1991) 3551.