| Transition Temperature | 70 K |
|---|---|
| Parent Space Group | Pm-3m (#221) |
| Magnetic Space Group | PIn-3n (#222.103) |
| Magnetic Point Group | m-3m1' (32.2.119) |
| Lattice Parameters | 7.33800 7.33800 7.33800 90.00000 90.00000 90.00000 |
|---|---|
| DOI | 10.1016/0304-8853(87)90539-7 |
| Reference | H. Fujii, Y. Uwatoko, K. Motoya, Y. Ito and T. Okamoto, Journal of Magnetism and Magnetic Materials (1987) 63-64 114-116. |
| Label | Element | Mx | My | Mz | |M| |
|---|---|---|---|---|---|
| Nd1 | Nd | 1.45 | 1.45 | 1.45 | 2.51 |
Title
NEUTRON DIFFRACTION AND MAGNETIC STUDIES OF CeZn AND NdZn SINGLE CRYSTALS
Authors
H FUJII, Y UWATOKO, T OKAMOTO Faculty of Integrated Arts and Sciences, Hroshuma University, Hiroshima 730, Japan
K MOTOYA Faculty of Science, Saitama University, Urawa 338, Japan
Y ITO Institute of Solid State Physics, University of Tokyo, Tokyo 106, Japan
Materials Studied
CeZn, NdZn, LaZn (for resistivity comparison)
Key Information
- Crystal structure / space group: CsCl-type structure (cubic)
- Magnetic ordering type and temperature:
- CeZn: Antiferromagnetic, \(T_N = 30\) K (first-order transition).
- NdZn: Antiferromagnetic, \(T_N = 70\) K (second-order transition). Exhibits a magnetic order-order transition at \(T_R = 18\) K (first-order transition).
- Propagation vector(s): \((0,0,\frac{1}{2})\) for both CeZn and NdZn.
- Magnetic moments:
- CeZn: \(1.91 \mu_B / R\)-atom (observed). Calculated as \(2.05 \mu_B\) at 8 K.
- NdZn: \(2.52 \mu_B / R\)-atom (observed). Calculated as \(2.60 \mu_B\) at 4.2 K.
- Lattice parameters: Not available.
- Other critical measured values:
- CeZn: \(\Gamma_8\) is the ground state. Tetragonal distortion below \(T_N\), with \((c/a-1)\) value reaching 17% at 80 K.
- NdZn: No tetragonal distortion. Below \(T_R\), Nd moments are directed along the \(\langle110\rangle\)-axes. Above \(T_R\), Nd moments are directed along the \(\langle111\rangle\)-axes.
Synthesis Method
Not available
Abstract
Neutron diffraction studies on CeZn indicate that the Ce moment is \(1.91\mu_B\) and \(\Gamma_8\) is the ground state. The observed Ce moment suggests that the Kondo effect should be considered, while magnetic properties of NdZn single crystal are qualitatively understood by taking into account the CEF effect.
Main Content Summary
This paper investigates the magnetic properties and crystal electric field (CEF) effects in CeZn and NdZn single crystals using neutron diffraction, magnetization, and electrical resistivity measurements. Both compounds crystallize in the CsCl-type structure and exhibit antiferromagnetism with a propagation vector of \((0,0,\frac{1}{2})\). The study highlights the distinct behaviors of CeZn, where Kondo effect plays a significant role, and NdZn, which is primarily governed by CEF effects.
For CeZn, neutron diffraction revealed a magnetic moment of \(1.91 \mu_B / R\)-atom, and the \(\Gamma_8\) state was identified as the ground state. A first-order magnetic transition occurs at \(T_N = 30\) K, accompanied by a tetragonal distortion below \(T_N\), where the \((c/a-1)\) value reached 17% at 80 K. Electrical resistivity measurements showed a discontinuity at \(T_N\) and a maximum in the magnetic resistivity, which is attributed to an incipient Kondo effect on the CEF-split multiplet. The observed magnetic moment was found to be smaller than the calculated value from a single-ion Hamiltonian, suggesting Kondo moment compensation.
NdZn exhibits a magnetic moment of \(2.52 \mu_B / R\)-atom and undergoes a second-order antiferromagnetic transition at \(T_N = 70\) K. Additionally, a first-order magnetic order-order transition is observed at \(T_R = 18\) K, characterized by a thermal hysteresis of approximately 2 K in resistivity. Magnetization curves indicate a change in the moment direction: below \(T_R\), Nd moments are along the \(\langle110\rangle\)-axes (non-collinear, Fig 1b), while above \(T_R\), they are along the \(\langle111\rangle\)-axes (non-collinear, Fig 1c). This reorientation supports a triple-q to double-q transition.
The magnetic properties of NdZn are well described by an effective single-ion Hamiltonian incorporating CEF parameters and exchange interactions, with calculated moments and moment directions agreeing fairly well with experimental observations. However, the calculated \(T_R\) was slightly higher than observed, suggesting the need for additional magnetoelastic or biquadratic exchange terms. In contrast, for CeZn, the discrepancy between observed and calculated moments, along with the poor fit of the M vs T curve, underscores the importance of considering the Kondo effect, where the Kondo temperature is not negligible compared to the CEF splitting.
Conclusion
Neutron diffraction studies on CeZn indicate that the Ce moment is \(1.91\mu_B\) and \(\Gamma_8\) is the ground state. The observed Ce moment suggests that the Kondo effect should be considered, while magnetic properties of NdZn single crystal are qualitatively understood by taking into account the CEF effect. For better understanding magnetism in CeZn, the Kondo effect should be considered since \(T_K\) is not negligible compared to the CEF splitting.
NEUTRON DIFFRACTION AND MAGNETIC STUDIES OF CeZn AND NdZn SINGLE CRYSTALS
H FUJII, Y UWATOKO, K MOTOYA, Y ITO* and T OKAMOTO
Faculty of Integrated Arts and Sciences, Hroshuma University, Hiroshima 730, Japan
Faculty of Science, Saitama University, Urawa 338, Japan *Institute of Solid State Physics, University of Tokyo, Tokyo 106, Japan
Neutron diffraction studies on CeZn indicate that the Ce moment is \( 1\ 91\mu_{B} \) and \( \Gamma_{8} \) is the ground state. The observed Ce moment suggests that the Kondo effect should be considered, while magnetic properties of NdZn single crystal are qualitatively understood by taking into account the CEF effect.
1. Introduction
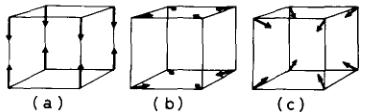
The equatomic compounds of the rare earth with zinc crystallize in the CsCl-type structure. The heavy-rare earth RZn compounds exhibit ferromagnetism, while the light-rare earth ones are antiferromagnetic. Powder neutron diffraction studies of the latter compounds \( [1,2] \) indicate that the magnetic structure is described by the propagation vector \( (0,0,\frac{1}{2}) \) with a quadratic magnetic cell \( (a,a,2a) \) . We consider only three different structures shown in fig 1 for cubic lattice as the \( (00\frac{1}{2}) \) magnetic reflection is absent, which are indiscernible on powder neutron patterns. However, as a tetragonal distortion is detected below \( T_{N} \) for CeZn and PrZn, we can deduce that the structure is the collinear-type structure (fig 1a). On the other hand, since NdZn does not show any distortion, it is impossible to determine the magnetic structure of NdZn from the neutron diffraction studies, assuming multidomains.
Among them, CeZn exhibits some anomalous behavior owing to possibly the extent of the 4f shell and the consequent strong mixing with the

Fig 1 Possible three equivalent magnetic structures in the cubic structure with the \( (00\frac{1}{2}) \) propagation vectors
conduction electron band states The especially interesting phenomena are (1) the appearance of pressure-induced ferromagnetism with a pronounced Kondo anomaly at high pressures above 8 kbar [3] and (2) the damping of the crystal electric field excitations (CEF) which lead to the collapse of the inelastic line into the quasi-elastic peak [4]
2. Results
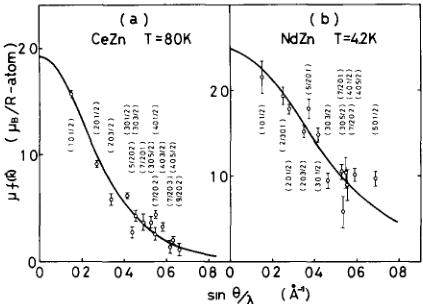
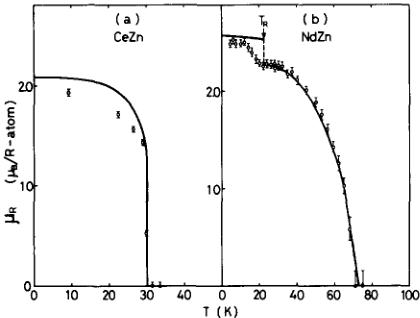
Fig 2 shows the product of the effective magnetic form factor by magnetic moment \( \mu f(\mathbf{k}) \) as a function of the scattering vector \( \sin\theta/\lambda \) ( \( \mathring{A}^{-1} \) ) for CeZn at 8 K and NdZn at 4 2 K. The form factor seems to be weakly anisotropic in CeZn, whereas that of NdZn is more anisotropic within our experimental errors. The magnetic moments of CeZn and NdZn are estimated to be 1 91 and \( 2\ 52\mu_{B}/R \) -atom by extrapolating \( \mu f(\mathbf{k}) \) to \( \sin\theta/\lambda=0 \) , respectively. These values are in good agreement with those obtained by Schmitt et al [1] and Morin and Pierre [2]. The temperature dependence of the magnetization is shown in fig 3 for both CeZn and NdZn, which were deduced from the \( (10\frac{1}{2}) \) magnetic reflections. CeZn reveals a first-order transition at \( T_{N}=30 \) K, below which a tetragonal distortion appeared and the \( (c/a-1) \) value reached 17% at 80 K from analysis of the (200) nuclear reflection. The magnetic moment of NdZn decreases sensibly near \( T_{R}=18 \) K and vanishes at \( T_{N}=70 \) K.

Fig 2 Effective magnetic amplitude \( \mu(\mathbf{k}) \) as a function of scattering vector \( \sin\theta/\lambda \) The solid lines show the calculated form factors according to the formula [6] \( f=\langle J_{0}\rangle+\sum_{i=2}^{4}C_{i}\langle J_{i}\rangle \) ( \( C_{2}=0 \) and \( C_{4}=0 \) 71 for CeZn, and \( C_{2}=0 \) 56 and \( C_{4}=0 \) for NdZn, respectively) The neutron diffraction experiments were performed for CeZn using PANSI of ISSP installed at the JRR-2 reactor, Tokai, JAERI and for NdZn using ND at the Research Reactor Institute, Kyoto University in Japan
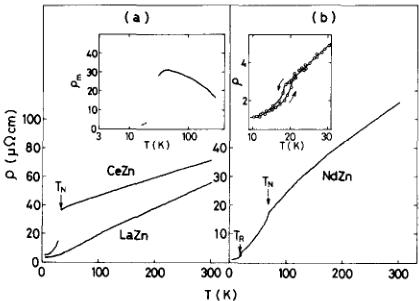
The electrical resistivities \( \rho \) of LaZn, CeZn and NdZn along the \( \langle100\rangle \) -axis are shown in fig 4 A remarkable discontinuity is observed for CeZn at \( T_{N} \) , which is characteristic of a first-order transition. The magnetic resistivity \( \rho_{m} \) for Ce was determined by subtracting the resistivity

Fig 3 Temperature dependence of magnetzaton deduced from the \( (10\frac{1}{2}) \) magnetic reflection for (a) CeZn and (b) NdZn The solid lines are the calculated ones using the Hamiltonian of eq (1)

Fig 4 Electrical resistivity \(\rho\) as a function of temperature \(T\) for (a) LaZn and CeZn, and (b) NdZn along the [100]-axis
of LaZn The temperature dependence of \(\rho_{\mathrm{m}}\) is given in the insertion of fig 4a The occurrence of a maximum in \(\rho_{\mathrm{m}}\) can be ascribed to an incipient Kondo effect on the CEF split multiplet of Ce This result is in agreement with that obtained by Pierre et al [4] The \(\rho\) vs \(T\) curve of NdZn reveals (1) an anomaly at \(T_{\mathrm{N}}\) corresponding to a second-order transition and (2) a well defined first-order transition at \(T_{\mathrm{R}}\) with a thermal hysteresis of \(\approx2\;\mathrm{K}\) as shown in the insert of fig 4b, suggesting a magnetic order-order transition
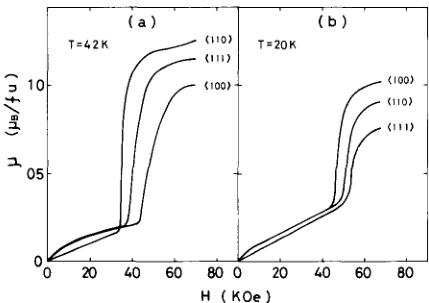
In order to obtain direct information on the order-order transition, we measured the magnetization curves along the \( \langle100\rangle \) , \( \langle110\rangle \) and \( \langle111\rangle \) -axes above and below \( T_{R} \) (see fig 5). The

Fig 5 Magnetization vs magnetic field curves of NdZn at (a) \( 4\ 2\ K < T_{R} \) and (b) \( 20\ K > T_{R} \) , where \( T_{R} \) is the reorientation temperature
metamagnetism below \( T_{R} \) can be interpreted by a non-collinear model with the Nd moments of \( 2\ 52\mu_{B} \) directed to the \( \langle110\rangle \) -axes (fig 1b), assuming that the Nd moments hold in the \( \langle110\rangle \) directions even though the field is applied to any directions because of strong magnetic anisotropy. The magnetic structure above \( T_{R} \) can be also understood by a non-collinear one with the Nd moments along the \( \langle111\rangle \) -axes (fig 1c) as discussed by Kitai et al [5] as well. These results give further confidence in the triple q to double q transition proposed by Morin and de Combarieu from the specific heat measurements [7].
3. Discussion
As is evident from fig 2, the form factor is weakly anisotropic in CeZn and the Ce moment is deduced as \( 1\ 91\mu_{B} \) . This indicates that \( \Gamma_{8} \) is the ground state. However, it is to be noted that the form factor decreases more sharply with increasing \( \sin\theta/\lambda \) than that expected from the ground state \( \left|\frac{5}{2},\frac{5}{2}\right\rangle \) , which could be realized in the ordered state at 8 K. On the other hand, the form factor of Nd is more anisotropic and it is possible to see that when the scattering vector is near the \( \langle100\rangle \) direction, the observed magnetic form factors are larger than those near the \( \langle110\rangle \) direction. This simply suggests that the 4f electron density along the \( \langle110\rangle \) direction is wider than along the \( \langle100\rangle \) direction. Then, the domain distribution was confirmed to be uniform from the intensity measurements of some equivalent \( \left\{\frac{1}{2}03\right\} \) magnetic peaks in the \( (h0l) \) plane, within our experimental errors.
As an attempt to explain the temperature dependence of magnetizations, we introduce the effective single-ion Hamiltonian as follows
\[ \begin{aligned}\mathcal{H}&=B_{4}(O_{4}^{0}+5O_{4}^{4})+B_{6}(O_{6}^{0}-21O_{6}^{4})\\&\quad-g\mu_{\mathrm{B}}J H_{\mathrm{e x}}-G_{1}(\langle O_{2}^{0}\rangle O_{2}^{0}+3\langle O_{2}^{2}\rangle O_{2}^{2})\end{aligned} \quad (1) \]
Here, \( B_{n} \) is the CEF parameter, \( H_{ex} \) is the bilinear exchange field which is given by \( H_{ex} = ng\mu_{B}\langle J\rangle \) and \( n = \theta^{*}/C \) , and the last term expresses the magnetoelastic and/or biquadratic exchange interactions. The Ce moment is estimated as \( 2\ 05\mu_{B} \) at 8 K in CeZn using \( \theta^{*} = 32\ K \) , \( G_{1} = 0\ 22\ K \) and \( B_{4} = 0\ 18\ K \) ( \( \Delta = 65\ K \) ) according to Pierre et al [4]. The calculated value is considerably larger than \( 1\ 91\mu_{B} \) obtained in this work. This difference might be attributed to the Kondo moment compensation, that is the Kondo-type antiparallel coupling between the 4f moments and conduction electron spins. Furthermore, we cannot satisfactorily understand the M vs T curve of CeZn shown in fig 3a, in which the solid line is the calculated value using the Hamiltonian of eq (1).
On the other hand, the Nd moment is calculated to be \( 2\,60\mu_{B} \) at \( 4\,2\,K \) using \( B_{4}=2\,4\times10^{-2}\,K \) and \( B_{6}=1\,4\times10^{-3}\,K \) , \( \theta^{*}=90\,K \) and \( G_{1}=0 \) , which is in fairly good agreement with the observed value of \( 2\,52\mu_{B} \) . The moment direction at \( 4\,2\,K \) is deduced to be along the \( (110) \) -axes and above \( T_{R}=24\,K \) , the Nd moments are directed to the \( (111) \) -axes under the condtion which minimizes the free energy. The Nd moment calculated is shown by the solid line in fig 3b. The agreement between the calculated curve and experimental points is fairly good, but the calculated \( T_{R} \) is a little higher than the observed \( T_{R}\approx18\,K \) . This suggests that not only \( G_{1} \) but also \( G_{2} \) terms must be taken into account, where the \( G_{2} \) term is expressed by \( G_{2}(\langle0xy\rangle0xy+\langle0yz\rangle0yz+\langle0zx\rangle0zx) \) .
On the other hand, for better understanding magnetism in CeZn, the Kondo effect should be considered since \( T_{K} \) is not negligible compared to the CEF splitting
References
[1] D Schmitt, P Morin and J Pierre, J Magn Magn Mat 8 (1978) 249
[2] P Morin and J Pierre, Phys Stat Sol (a)30 (1975) 549
[3] H Kadomatsu, H Tanaka, M Kurisu and H Fujiwara, Phys Rev B33 (1986) 4799
[4] J. Pierre, A P. Murani and R M. Galera, J. Phys F11 (1981) 679
[5] T. Kitai, H. Fujii, T. Okamoto and Y. Hashimoto, Solid State Commun 52 (1984) 407
[6] M. Blume, A J. Freeman and R E. Watson, J Chem Phys 37 (1962) 1245
[7] P. Morin and A. de Combarieu, Solid State Commun 17 (1975) 975